How to solve C and D?
I think I have seen the problem J somewhere before
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 02:37:10 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How to solve E and H? They are both pretty interesting problem.
H:
First of all, we can ask n queries to find all leaves of the tree. To check whether a vertex is a leaf, we ask a query containing all n - 1 other vertices; if the answer is n - 1, the vertex we excluded from a query is a leaf.
Then let's root our tree at some leaf. Let L(x) be the set of leaves in the subtree of vertex x. Since there are no vertices with degree 2, for any two vertices x and y L(x) ≠ L(y); furthermore, x is an ancestor of y iff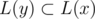 . So if we obtain the information about L(x) for every vertex, then we can reconstruct the tree.
. So if we obtain the information about L(x) for every vertex, then we can reconstruct the tree.
For the root, L(root) is the set of all leaves. For every other leaf z, L(z) = {z}. So we need to find L(x) only for non-leaves. To check whether a leaf z is in a subtree of non-leaf vertex y, we may ask a query 3 root y z.
So if the number of leaves is l, we have to ask (l - 1)(n - l) queries to find L(x) for all non-leaf vertices. This won't exceed 2450, and so we won't ask more than 2550 queries.
Cool! It is a really simple solution.
We had solution we the same queries but second part used different perspective.
So, for each leaf we know the "path" to the root (only vertices, not their order). Now intersection of any two such "paths" is also path to the root from some vertex(their lca). And each vertex is lca of 2 leaves (because of no 2-degree vertices). So now we have list of "paths" for all vertices and need to reconstruct tree which may be done by simple dfs.
If the tree is a bamboo, answers for all queries of the first part of the algorithm should be n - 1, shouldn't it? If no, please explain why.
E : In DAG every node can be reached by A and reach B, iff
Now you should select two disjoint edge set EA, EB such that
This can be found by maximum matching in O(mn0.5)
Wow, flow for 1000000 edges, that's a new record I've ever seen :)
By the way it can be solved without flow.
I don't understand why it's a new record for you, but bipartite matching on 10^6 vertices should obviously run on time :)
Clearing the graph for every TC was a pain, though.
Also, it can be done in O(m), and even it can be done with minmal total cost of edges in O(m) time.
Let's add two edges from B to A. Now we have only a condition on degrees. Lets get a bipartite grpah with 2 copies of vertices in left part (corresponding to vertex in EA and to vertex in EB) and edges in right part. Every vertex in second part will have exactly two edges (to start in EA and to and in EB). The problem is to find perfect (by left part) matching in this graph.
This can be done in two ways. First, every chain we are searching for in Kuhn method have unique edge on each step. So we can just maintain end of this chain for each vertex in disjoint set union.
The other way, which seem to be more beautiful for me, is think about vertex of degree 2 as about an edge between it's neighbors. It can be shown, that matching is same as covering this graph by set of edges, where no component have more edges then vertices (that is a tree, or a cycle with trees on it). Such covering can be done by something like Kruskal algorithm. And two be honest, produces exactly the same code, that first method.
And if we sort edges by increasing of cost in any of this methods, it will lead us to min-cost solution.
Anyone know the intended solution to B? How are you supposed to do the computations quickly after arriving at a formula for the answer?
While I haven't got AC, I got something in python that might pass in a faster language with builtin GMP-gcd with some constant optimizations.
Let 'avgbad' be the average cost of an unreasonable item and 'avgreason' be the average cost of a reasonable item. Let 'bads' be the number of unreasonable items. Then the answer is
(The formula can be gotten with some calculations and [this](https://www.wolframalpha.com/input/?i=sum_%7Bk%3D1%7D%5E%7Bm%7D+binom(b,+k)%2Fbinom(n,+k)) Identity.)
The binomials can be computed quite a bit faster by sieving over primes, this could probably be speed up more by computing the product in divide&conquer fashion. The main bottleneck was reducing the fraction. The buitin python gcd is to slow, I found a faster lehmer-gcd here, but it's still to slow.
Loading GMP into c++ does not work on Yandex unfortunately (at least the method that works on spoj doesn't work on yandex), so I couldn't try GMP-gcd. I'll try some more stuff tomorow.
Edit: Got some speedup in pow_binomal by computing the product in a smarter way, now TLE 36 (previously TLE 34).
Alright, I got AC in 1.5s with some more optimizations.
Optimizations used:
Oh my...
You're awesome :)
How to solve problem F? How do we use the constraint of ?
?
I think we need to use the trick from here, if we choose a random index and with probability (which by our condition is at least
(which by our condition is at least  so we'll check around 10 cases to be sure) it will appear in the final sequence. Then we find its biggest divisor such that there are at least n - k numbers that divide this number.
so we'll check around 10 cases to be sure) it will appear in the final sequence. Then we find its biggest divisor such that there are at least n - k numbers that divide this number.
UPD. About the last part, suppose we chose number N, it has at most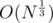 divisors. Suppose its divisors are 1 = d1 < d2 < ... < dK = N and prime numbers the divide it are p1 < p2 < ... < pt (1 ≤ t ≤ 15). We'll calculate an array cnt with cnti being the number of values in our sequence that divide di. In the problem mentioned above we are allowed to do the following thing:
divisors. Suppose its divisors are 1 = d1 < d2 < ... < dK = N and prime numbers the divide it are p1 < p2 < ... < pt (1 ≤ t ≤ 15). We'll calculate an array cnt with cnti being the number of values in our sequence that divide di. In the problem mentioned above we are allowed to do the following thing:
First set cnti to be equal to the number of values such that gcd between it and N is equal to i.
Second, just iterate for every i from K downto 1 and for every j from i + 1 to K if we have that dj ≡ 0 (mod di) then we increase cntj by cnti.
Now we need to optimise it because O(K2) is too much, that's why I introduced the sequence of primes. Basically for every prime pi and for every j we increase by cntj the position in array cnt corresponding to the divisors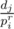 (1 ≤ r, dj ≡ 0 (mod pir)). This can be done again in linear time. So the complexity becomes
(1 ≤ r, dj ≡ 0 (mod pir)). This can be done again in linear time. So the complexity becomes 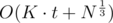 which in practice is way smaller.
which in practice is way smaller.
If you find something wrong, please let me know. I hope I didn't miss any easy solution :) .
I got accepted with following heuristic.
If n is less than 80, just factorize all numbers and solve the problem. Else, let's get 80 random numbers, factorize them, and get all divisors that are in at least 16 of them. For each of this divisors starting with big solve the problem in time O(number of diffrent numbers).
Idea is that probably, if we have many big numbers which are divisors of a lot of random numbers, but of n - k numbers, we have a lot of same numbers in input. No idea about formal proofs.
C: On the line this problem could be solved with simple greedy: take a path with the leftest right end, take it's right end, delete all the paths that contain this point and repeat until we cover all paths. On the tree the same greedy works, except we always take a path with the lowest lca.
D: Let dpi be answer for the i-th prefix. Then dpi = minj < i(max(t[i], dp[j]) + 2 * maxj < k ≤ i(ak)). Notice that dpi is nondecreasing. Then there exists pos such that dpj < ti for j < pos and dpj ≥ ti for j ≥ pos. We can maintain pos with 2 pointers. Now we can consider j < pos and j ≥ pos separately. For j < pos we need to calculate minj < pos(ti + 2 * maxj < k ≤ i(ak)). We can mantain segment tree where j-th value is maxj < k ≤ i(ak) and update it easily with stack of maximums. The case j ≥ pos is almost the same.
How to solve J?
How to solve J faster than O(nm3) or O(nlognm2) ?
I found the solution just after asking it : the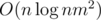 approach actually runs in
approach actually runs in 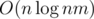 , and the problem is almost the same as problem K from http://codeforces.com/blog/entry/55467
, and the problem is almost the same as problem K from http://codeforces.com/blog/entry/55467
(Maybe that's the same thing you described in previous comment, but) We did it in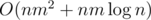 :
:
Using divide and conquer, fix center of the array. All the queries are either to the left or to the right or goes through the center. THose to the left and to the right we will do recursively. Now, from the center calculate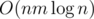 for divide&conquer part
for divide&conquer part
dp[l:center]anddp[center:r]for all l and r in O(nm) Now for each query you'll answer in O(m2). So, overall complexity is O(nm2) for queries (well, O(qm2) but who cares) andIsn't it O(qm)? if you let modulo as x on left part, then modulo on right part is (m - x)
Thanks. What we actually submitted was O(qm2) but you are right, it is easier to do in O(qm)
I :
Suppose you can afford a trie on given strings, then you can try DP on tree. DP[i] = (number of subset for subtree of i). Then you have simple recurrences.
Our solution is online. We will build a tree from a set of string S, where a parent of node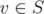 is a longest prefix that is not v and in S. Basically this is a sort of compressed trie, so you can try identical DP if you have this one.
is a longest prefix that is not v and in S. Basically this is a sort of compressed trie, so you can try identical DP if you have this one.
We sort all strings in lexicographical order (done by suffix array). This will be a preorder traversal of such tree. With suffix array you can find whether given two substrings are prefix or not — you can decide whether string x is an ancestor of string y. Now you can use stack to iteratively make a tree.
Time complexity : O(nlogn + qlogn)
G: Do a binary search for T. Rearrange the inequality to oaj ≤ obj + T - dj. This corresponds to an edge bj → aj with weight T - dj when interpreting ox as the distance to x. Initialize the o as given in the input and replace '?' by 109. Run Bellman-ford, if a negative cycle is found or one of the given o changes, T is too small.
L: Use Dijkstra's to compute all edges that are in some shortest path starting at the capital. Then use the solution of problem C from GP of Poland to get the number of edges which are used in all shortest paths to a given node.
K: I have solution in with rolling hashes and the fact the the query strings can have at most
with rolling hashes and the fact the the query strings can have at most 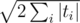 different lengths. Is there something faster?
different lengths. Is there something faster?
For F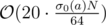 passes in 2s if you use bitset and prune divisor candidates that are smaller than the current best or that are divided by an already discarded candidate when generating the divisors of a recursively from the prime factors.
passes in 2s if you use bitset and prune divisor candidates that are smaller than the current best or that are divided by an already discarded candidate when generating the divisors of a recursively from the prime factors.
K: You can do with the same complexity but with trie and kmp, you build a trie for every word in the set that has length smaller than for every node in the trie you keep the the current answer and the last index last of the occurrence then updates this values running in the substrings of size smaller than
for every node in the trie you keep the the current answer and the last index last of the occurrence then updates this values running in the substrings of size smaller than  of the text and for the rest of the strings in the set you do kmp. I don't know if it's faster, passed with 275 ms
of the text and for the rest of the strings in the set you do kmp. I don't know if it's faster, passed with 275 ms
Actually, you can skip part with KMP. If you'll go in trie by suffix links, you can visit only sqrt(M) terminate (in which ends some word from input) nodes, where M is sum of words lengths.
I am getting TLE on TC-15 by using rolling hashes for problem K.
What I did was precompute the hash function for every prefix of S and for every query compute the hash for query substring P and traverse through S and greedily pick matches. I also stored the answers for every query in a map to avoid recomputation. What am I missing?
118728564
If the query strings are all short and distinct, then caching the answers in a map doesn't help, so your solution loops over the entire string $$$s$$$ for every query, resulting in a total running time of $$$\Omega(n m)$$$, which is too slow.
The key idea for my solution is to process all strings of the same length simultaneously in a single pass over $$$s$$$. Then the total number of passes over $$$s$$$ is at most $$$\sqrt{2 \sum_i |t_i|}$$$, which is a lot less than $$$m$$$.
Is there any easy to code solution for A?
Count each triplet at its smallest element. When fixing the smallest element x, the other two elements need to be in [x, x + d], so we can count them with binary searches on the two other arrays. Slight care has to be taken to not count triplets with duplicate elements multiple times.
It may also be done in O(n) with two pointers technique insted of binary search (it also helps to take care of equal minimums automatically)
My problems are E and G. Hope you liked it!
E is very cool, G is good, but isn't fresh. I am sure that already have seen it.
Where can we access the problem statements? Can you please provide me with the link to the problem set?
It's here
BTW, statement of most opencup rounds can be found here some times after the contest.
Can you please tell me, where can we submit our solutions to above problems?
You can submit your code to me, I will review your code and give you a verdict (Accepted/ Wrong Answer/ Time limit exceeded/ Presentation error)
The contest is also in Codeforces gym here where you can submit.