What is the fastest algorithm to compute maximal bipartite matching. What is its worst case run time complexity. How to construct the worst case for such algorithm. Thanks in advance.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 23:59:14 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










The fastest is Hopcroft Karp BPM. It runs in O(sqrt(v)*E). You can go through Wikipedia to learn more.
Do you know In what case it is slow? I think on random graphs it runs pretty fast
I bet this guy knows something about it: Burunduk1
In d-regular graph (all degrees are equal to d) there is O(nlogn) algorithm Goel, Kapralov, Khanna. Notice, asymptotic is independent of number of edges. The algorithm: consider graph, on which Kuhn runs dfs, and instead of dfs run "random walk" (choose random edge and go throw it).
On random but not regular graphs Kuhn with optimizations is better than Hopcroft.
Bipartite Matching problem is equivalent to max flow in a modified graph.
In graphs which are dense locally at some places and mostly sparse overall, Push Relabel Algorithm with gap Relabel heuristic runs very very fast. Much faster compared to Dinic's (which is equivalent to Hopcroft Karp).
Asymptotic complexity of such algorithm is O(|v|^3) though for general graphs. But on random graphs it runs much more fast. To give you some numbers — my implementation runs within seconds for random graphs with n = 10000 nodes, m = 1000000 edges.
it would be great if you could share your implementation code.
...
If you use the lowest-label version and use global relabeling, the runtime can be bounded by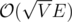 (see Robert J. Kennedy, Jr. Solving unweighted and weighted bipartite matching problems in theory and practice, chapter 3 (The paper does not treat gap relabeling.)).
(see Robert J. Kennedy, Jr. Solving unweighted and weighted bipartite matching problems in theory and practice, chapter 3 (The paper does not treat gap relabeling.)).
Even without global relabeling, the lowest label version is usually the fastest one on bipartite matching graphs.
Thanks for sharing. Not so obvious at the moment though, I will ponder on this :)
One can also use Dinic algo and reduce problem to max flow, that will be as fast as Hopcroft Karp on bipartite graphs.
You might want to check out this variation of the alternating paths bipartite match algorithm. It is easy to code and very quick for most networks that have particularities (it can do ~1e6 vertices and edges in considerably less than 1s), even quicker than the regular Hopcroft-Karp algorithm (because it doesn't do any bfs beforehand).
Code: https://pastebin.com/q12aBwya
Note that the key optimization here is in the separation of the two for loops.
I have yet to find an example where it does quadratic time (and I think it's very non-trivial). I however suspect that the proof of Edmonds Karp upper bound cannot be applied here, as what the algorithm is doing is not equivalent to a BFS (the alternating paths aren't shortest, per se).
Your implementation has got an Ω(V2) worst case on a sparse graph (E = Θ(V)).
The input is approximately n, the output is n m followed by m edges. The vertices on either side are zero-based.
The input is a tree consisting of a long path of length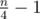 and paths of length 3 hanging from every vertex in the long path. Vertex labels and edge order are chosen in a way such that initially every other edge in the long path is matched and every middle edge in a short path is matched. In a single phase, you'll find a single long augmenting path, alternating left → right and right → left. (The paths of length 3 break your heuristic.) This results in
and paths of length 3 hanging from every vertex in the long path. Vertex labels and edge order are chosen in a way such that initially every other edge in the long path is matched and every middle edge in a short path is matched. In a single phase, you'll find a single long augmenting path, alternating left → right and right → left. (The paths of length 3 break your heuristic.) This results in 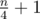 phases.
phases.
The lower bound can be extended to Ω(VE) by adding a dense part K2x, x with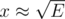 where you'll scan x2 ≈ E edges every phase.
where you'll scan x2 ≈ E edges every phase.
You might be able to fix this by randomizing the vertex and edge ordering.
Thank you for your counterexample!
As weird as this sounds, this implementation is the one that basically every high-school student in our country learns about as being the Hopcroft-Karp algorithm, and nobody here has managed to find a counterexample to break the heuristic (I think mostly because I am not very familiar with how to generate maximal test cases for matching in general).
I will try to add this example to our most popular online judge archive. This should be fun.
It seems like randomizing the order of vertices drops down the number of iterations to 8 in this case, although it's (very slightly) slower because of the shuffle algorithm. It's good to note though.