Three cases are sufficient to solve this problem.
1) m = n = 0, the answer is “0 0”;
2) n = 0, m > 0, the answer is “Impossible”;
3) none of above, the answer is n + max(m - n, 0) and n + m - 1.
Without loss of generality, we assume that radius r1 > r2 and the distance between their centers is d. The problem can be solved based on the following cases.
1) two circles have at least one common point: the answer is r = 0 since it can be put at any one the common point(s).
2) one circle is exactly outside the other one: the answer is 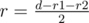 .
.
3) one circle is exactly inside the other one: the answer is 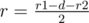 .
.
Besides, one should carefully deal with the precision problem. For instance, when we try to check whether d < r1 + r2 holds or not, we should compare (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) < (r1 + r2) * (r1 + r2) since only integers are involved here, which gives strictly precise result.
We can enumerate the type (“pair” or “int”) in the given order one by one, while using a “stack” s to maintain the current “state”.
In details, when we meet a “pair”, we output “pair<” and push an integer 2 to the stack. The reason is that if this is a reasonable sequence, then “pair” means a new start and it must be “pair<”. We push 2 to the stack to indicate that we need wait for another two “types” to complete the current “pair”.
On the other hand, when we meet an “int”, we check whether the “stack” is empty or not. If yes, it means that there must be only one “int” (also implies that n = 1) and zero “pair”, and we only output “int” (note that this case might also occur if it is not a reasonable sequence, for instance “pair int int int”, however we have other methods to tell this, which will be mentioned later). If no, then we take out the top integer in the “stack”. If it is 2, it means that the current “int” serves as the first part of the last “pair” which is still not completed. Thus, we should output “int,” and set the top integer to 1, as we have obtained the first part and only need wait for the second one. If the top integer is 1, it means that the current “int” serves as the second part of the last “pair”. Thus, we should output “int>,” and pop out the top integer of the “stack”. Next, notice that the last “pair” has been completed and it may serve as the first part of some other “pair”. Hence, we should further check the top integer of the “stack”, and if it is 1, we output “>” to complete the current “pair” and pop out the top integer. We keep the above process until the “stack” is empty or the top integer is 2, and if the latter case occurs, we should output “,” and set the top integer as 1.
After finishing the above process, the sequence is reasonable if the following two conditions are fulfilled. The stack is empty and the number of “pair” is strictly one less than that of “int”.
A classical “two pointers” problem. We use one pointer s to point to the starting point while using the second pointer t (t > s) to point to the minimum position so that there exists at least one integer which has appeared exactly k times, within the interval [s, t - 1]. We move these two pointers to find out all such intervals, and for each of them, it contributes n + 1 - t (index starts from zero) to the final answer.
The left work is to determine whether for some interval [s, t - 1], it can meet the requirements or not. We can use a segment tree which maintains the maximum number of appearance of integers [l, r], to accomplish this. Do not forget to compress all the input data to a smaller range so that segment tree is feasible. When we move s one step forward, we decrease the number of appearance of integer a[s] by one in the segment tree and complete the updating of other nodes. When we move t one step further, we implement similar updating. The value stored in the root node is just the maximum number of appearance of some integer within the current sliding window.
I followed the idea mentioned in tutorials.
At first, we insert all the node indices into a “set”. Then, we adopt three loops to solve the problem.
loop 1: as long as the “set” is not empty, we always take out the first element and push it to a “queue”. Then we erase it from the “set” and go to loop 2;
loop 2: as long as the “queue” is not empty, we take out the first element u (remember to pop it out from the “queue”) and go to loop 3;
loop 3: we enumerate every element that is still in the “set” and use binary search to check whether it is connected to u. If no, we push this element to “queue”, and erase it from the “set” (it seems to be a good idea if we store all these elements first and then erase them when we return back to loop 2).
I think the above algorithm has complexity of order (m + n)logn (worst case), which can be computed based on amortized analysis.









