My solution is to first calculate all the integers that have a form of 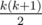 while not exceeding 109. Then, for the given integer n, we can enumerate the first term from the previously obtained results and check whether their difference is also an integer that we have computed, which can be implemented based on binary search. The total complexity is thus O(NlogN).
while not exceeding 109. Then, for the given integer n, we can enumerate the first term from the previously obtained results and check whether their difference is also an integer that we have computed, which can be implemented based on binary search. The total complexity is thus O(NlogN).
We can test the threshold from small values to large ones. For each threshold, we check whether the first and last elements are both still “accessible” (event-1), and further check whether there are two consecutive elements, except for the first and last ones, that are not “accessible” (event-2). We find the maximum threshold that event-1 is true and event-2 is false.
The basic idea is dp. We use dp[i][j] to denote the maximum length that we can obtain while using all the given strings, with starting letter “i” and ending letter “j”. The recursive formula is as follows:
When we meet a new string s, with starting letter “k” and ending letter “j”, we should update all dp[i][j] with i = 0, 1, ..., 25, according to dp[i][j] = max(dp[i][j], dp[i][k] + length(s)), as long as dp[i][k] > 0 (this means that we have found some combination of strings that starts with letter “i” and ends with letter “k”). Besides, string s can also serve as the first string, and thus we should further update dp[k][j] = max(dp[k][j], length(s)).
Finally, we should find out the maximum value of dp[i][i] as the answer.
Notice that the last element does not affect the result. We first sort the other n - 1 elements in a decreasing order, and compute the sum of the first k terms as ks. If ks ≤ b, it means that we have no choice but to select the last element. The reason is that they have enough money to reject any choice unless we select the last one.
On the other hand, if ks > b, it implies that we have a chance to obtain a better result. At first, as ks = a[1] + a[2] + ... + a[k] > b (index starts from “1”), it means that we can select any one of their original indices (remember that they have been sorted and thus we should find their “true” indices) as the final result, since b - (a[1] + a[2] + ... + a[j - 1] + a[j + 1] + ... + a[k]) < a[j] holds for any j and our final choice can not be rejected. Besides, we also have a chance to select any one of the other n - k - 1 (the last one is excluded) indices as our final result. It is obvious that we should first try a[1], a[2], ..., a[k - 1] so that the administration has the least money with a value of b - (ks - a[k]) to reject our final choice. Therefore, we can test the other n - k - 1 indices and check whether their cost is larger than b - (ks - a[k]), and if yes, then we can select it.
We keep updating the “best” result according to the above steps and finally output the answer.
A classical LCA problem.
At first, we should figure out how to calculate LCA of any given two nodes with compleixty of order logN. There are several classical algorithms to solve this and as one can find a large number of materials talking about this, we omit the details here. As for me, I used dfs to build a “timestamp array” and implemented RMQ to calculate LCA.
Next, we use dis[u] to denote the number for which the edges from u to the root node have been visited (quite similar to prefix idea). For instance, dis[u] = 2 means that every edge from u to the root node has been visited for two times.
For each query with given nodes u and v, we should imcrease dis[u] and dis[v] by one, respectively while decreasing dis[LCA(u, v)] by two. One can draw a simple graph and check this with paper and pen.
After dealing with all the queries, we are going to calculate the times for which each edge has been visited. To obtain a correct result, we should visit dis[u] in a decreasing order of the depth of u, and whenever we complete a node u, we should add dis[u] to its parent node. For instance, u is a leaf node and also serves as a child node of node v. Then, the edge between u and v has been visited for dis[u] times, and we update dis[v] as dis[v] = dis[v] + dis[u]. The reason is that any edge from v to the root node is counted both in dis[v] and dis[u], as it belongs to two prefix arrays.









