Suppose that we have m exams with value 2. Then, we have 2m + 3(n - m) ≤ k ≤ 2m + 5(n - m). As the problem guarantees that there is at least one reasonable answer, we have m ≥ 3n - k. Therefore, the answer should be max(3n - k, 0).
An intuitive understanding of the above result is that we can first assign 3 to all the n exams. If 3n ≤ k, it means that we can assign the extra k - 3n values to some exams and we have zero 2s. On the other hand, we have 3n > k, and thus we have to “set” at least 3n - k exams from 3 to 2.
By some simple induction, one can see that we should find the minimum positive integer k so that k(n + 1) is a multiple of 4n. The result is that 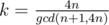 .
.
Let the number of “#” is k. If k ≤ 2, the answer is “impossible” (check the problem description). Otherwise, we check whether there is at least one cut point or not. If yes, the answer is obviously 1 since we can remove the cut point. If no, it suffices to remove two points to break the connectivity (this result seems quite intuitive and one can check the tutorials for proof). We can use tarjan's algorithm to find the cut point if there is any.
The trick is that any k consecutive “xor” operations is equivalent to either one single (k is odd) or zero “xor” operation (k is even).
Thus, we can use dfs to solve this. We build a dfs function with input res and flag, where res denotes the total number of operations that we still can implement, and flag denotes whether the last operation is a single (flag = 1) or zero (flag = 0) “xor” operation. Whenever we enter the dfs function, we first set all the remaining res operations as “xor” and calculate a value and update the maximum answer. Then, we check the value of flag and if flag = 0, we can implement one single “xor” operation and recursively call this dfs function with res - 1 and flag = 1. However, no matter what the value of flag is, we should always call dfs once again with res - 1 and flag = 0. Be careful that, as usually done in dfs with backtracing, we should record the “state” before we call dfs again, while after calling, we should restore the state.
I learned from the turotials.
Supoose that we write the first sequence s1[n] in the first row, the second sequence s2[n] in the second row, and so on, which finally forms a matrix (this is straightfoward). For each column, it can be viewed as a sequence of length 4, consisting of 0 and 1. We first give an intuitive example to show how the tutorials work. For a column (1 0 1 1), i.e., s1[i] = 1, s2[i] = 0, s3[i] = 1, s4[i] = 1, after six “xor” operations (according to the order), it gives (1 0 0 1 1 0), i.e., 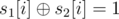 ,
, 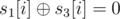 , and so on. Similarly, for a column (0 1 1 0), it gives (1 1 0 0 1 1). Based on the above examples, we can see that the column can have 24 = 16 different sequences, which correspond to 16 “xor operation sequence”. Thus, as the final matrix has 4 rows and m columns, each column must be one of the 16 sequences, and we can further build another matrix with 6 rows and m column, and the i-th column is just the “xor operation sequence” of the i-th column in the 4 × m matrix. Next, suppose that the number of each “xor operation sequence” involved in the 6 × m matrix is x1, x2, ..., x16. Then, we can build an equation Ax = b, where A is a 6 × 16 matrix consisting of the 16 “xor operation sequence”, x is just the vector (x1, x2, ..., x16) and b is a vector of length 6, just the given six values in the problem. Now, the problem is reduced to solving such a linear equation with 16 variables and 6 equations.
, and so on. Similarly, for a column (0 1 1 0), it gives (1 1 0 0 1 1). Based on the above examples, we can see that the column can have 24 = 16 different sequences, which correspond to 16 “xor operation sequence”. Thus, as the final matrix has 4 rows and m columns, each column must be one of the 16 sequences, and we can further build another matrix with 6 rows and m column, and the i-th column is just the “xor operation sequence” of the i-th column in the 4 × m matrix. Next, suppose that the number of each “xor operation sequence” involved in the 6 × m matrix is x1, x2, ..., x16. Then, we can build an equation Ax = b, where A is a 6 × 16 matrix consisting of the 16 “xor operation sequence”, x is just the vector (x1, x2, ..., x16) and b is a vector of length 6, just the given six values in the problem. Now, the problem is reduced to solving such a linear equation with 16 variables and 6 equations.
Nevertheless, some of these 16 “xor operation sequence” are the same. For instance, one can check that both (0 1 1 0) and (1 0 0 1) will give (1 1 0 0 1 1). Therefore, some of the variables can be combined to one single variable. After some simple compution (or write extra codes to accomplish this), the original equation can be further reduced to 7 variables and 6 equations. To solve this, we can enumerate the value of any one of the 7 variables, while solving the remaining 6 ones by gaussian elimination, and find out the optimal answer.









