Tutorial is loading...
Set by : vntshh
Setter's solution
#include<bits/stdc++.h>
#define rep(i,start,lim) for(lld i=start;i<lim;i++)
#define repd(i,start,lim) for(lld i=start;i>=lim;i--)
#define scan(x) scanf("%lld",&x)
#define print(x) printf("%lld ",x)
#define f first
#define s second
#define pb push_back
#define mp make_pair
#define br printf("\n")
#define sz(a) lld((a).size())
#define YES printf("YES\n")
#define NO printf("NO\n")
#define all(c) (c).begin(),(c).end()
#define INF 1011111111
#define LLINF 1000111000111000111LL
#define EPS (double)1e-10
#define MOD 1000000007
#define PI 3.14159265358979323
using namespace std;
typedef long double ldb;
typedef long long lld;
lld powm(lld base,lld exp,lld mod=MOD) {lld ans=1;while(exp){if(exp&1) ans=(ans*base)%mod;exp>>=1,base=(base*base)%mod;}return ans;}
lld ctl(char x,char an='a') {return (lld)(x-an);}
char ltc(lld x,char an='a') {return (char)(x+an);}
#define bit(x,j) ((x>>j)&1)
typedef vector<lld> vlld;
typedef pair<lld,lld> plld;
typedef map<lld,lld> mlld;
typedef set<lld> slld;
#define sync ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define mxm(a,b) a = max(a,b)
#define mnm(a,b) a = min(a,b)
#define endl '\n'
#define fre freopen("1.in","r",stdin); freopen("1.out","w",stdout);
#define N 1000005
int main()
{
//sync;
string s;
map<char,lld> m;
cin>>s;
lld k = sz(s);
string tmp = "";
tmp += s[0];
rep(i,1,k) if(s[i]!=s[i-1]) tmp+=s[i];
rep(i,0,k) m[s[i]]++;
if(tmp != "abc") return 0*NO;
if(m['c']!=m['a'] and m['c']!=m['b']) return 0*NO;
if(m['a']>=1 and m['b']>=1) return 0*YES;
else return 0*NO;
return 0;
}
Tutorial is loading...
Set by : AakashHanda
Setter's solution
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
priority_queue<ll> pq;
int main(){
int n, k1, k2, k;
cin>>n>>k1>>k2;
k = k1+k2;
vector<ll> a(n), b(n), arr(n);
for(int i=0 ; i<n ; ++i)
cin>>a[i];
for(int i=0 ; i<n ; ++i){
cin>>b[i];
arr[i] = abs(a[i]-b[i]);
pq.push(arr[i]);
}
while(k>0){
ll curr = pq.top();
pq.pop();
pq.push(abs(curr-1));
k--;
}
ll ans = 0;
while(!pq.empty()){
ll curr = pq.top();
ans += (curr*curr);
pq.pop();
}
cout<<ans;
}
Tutorial is loading...
Set by : 7dan
Setter's solution
#include<bits/stdc++.h>
#define rep(i,start,lim) for(lld i=start;i<lim;i++)
#define repd(i,start,lim) for(lld i=start;i>=lim;i--)
#define scan(x) scanf("%lld",&x)
#define print(x) printf("%lld ",x)
#define f first
#define s second
#define pb push_back
#define mp make_pair
#define br printf("\n")
#define sz(a) lld((a).size())
#define YES printf("YES\n")
#define NO printf("NO\n")
#define all(c) (c).begin(),(c).end()
#define INF 1011111111
#define LLINF 1000111000111000111LL
#define EPS (double)1e-10
#define MOD 1000000007
#define PI 3.14159265358979323
using namespace std;
typedef long double ldb;
typedef long long lld;
lld powm(lld base,lld exp,lld mod=MOD) {lld ans=1;while(exp){if(exp&1) ans=(ans*base)%mod;exp>>=1,base=(base*base)%mod;}return ans;}
lld ctl(char x,char an='a') {return (lld)(x-an);}
char ltc(lld x,char an='a') {return (char)(x+an);}
#define bit(x,j) ((x>>j)&1)
typedef vector<lld> vlld;
typedef pair<lld,lld> plld;
typedef map<lld,lld> mlld;
typedef set<lld> slld;
#define sync ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define mxm(a,b) a = max(a,b)
#define mnm(a,b) a = min(a,b)
#define endl '\n'
#define fre freopen("1.in","r",stdin); freopen("1.out","w",stdout);
#define N 1000005
int main()
{
//sync;
lld x,d;
vector<lld> ans;
cin>>x>>d;
lld num = 1, cnt = 0;
repd(i,60,1) if(bit(x,i)) {
rep(j,0,i) ans.pb(num);
cnt++;
num+=(d+1);
}
while(cnt--) ans.pb(num),num+=(d+1);
if(x%2) ans.pb(num);
cout<<sz(ans)<<endl;
for(auto i:ans) cout<<i<<" ";
return 0;
}
Tutorial is loading...
Set by : Vicennial
Setter's solution
//Gvs Akhil (Vicennial)
#include<bits/stdc++.h>
#define int long long
#define pb push_back
#define eb emplace_back
#define mp make_pair
#define mt make_tuple
#define ld(a) while(a--)
#define tci(v,i) for(auto i=v.begin();i!=v.end();i++)
#define tcf(v,i) for(auto i : v)
#define all(v) v.begin(),v.end()
#define rep(i,start,lim) for(long long (i)=(start);i<(lim);i++)
#define sync ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define osit ostream_iterator
#define INF 0x3f3f3f3f
#define LLINF 1000111000111000111LL
#define PI 3.14159265358979323
#define endl '\n'
#define trace1(x) cerr<<#x<<": "<<x<<endl
#define trace2(x, y) cerr<<#x<<": "<<x<<" | "<<#y<<": "<<y<<endl
#define trace3(x, y, z) cerr<<#x<<":" <<x<<" | "<<#y<<": "<<y<<" | "<<#z<<": "<<z<<endl
#define trace4(a, b, c, d) cerr<<#a<<": "<<a<<" | "<<#b<<": "<<b<<" | "<<#c<<": "<<c<<" | "<<#d<<": "<<d<<endl
#define trace5(a, b, c, d, e) cerr<<#a<<": "<<a<<" | "<<#b<<": "<<b<<" | "<<#c<<": "<<c<<" | "<<#d<<": "<<d<<" | "<<#e<< ": "<<e<<endl
#define trace6(a, b, c, d, e, f) cerr<<#a<<": "<<a<<" | "<<#b<<": "<<b<<" | "<<#c<<": "<<c<<" | "<<#d<<": "<<d<<" | "<<#e<< ": "<<e<<" | "<<#f<<": "<<f<<endl
const int N=1000006;
using namespace std;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef long long ll;
typedef vector<long long> vll;
typedef vector<vll> vvll;
typedef long double ld;
typedef pair<int,int> ii;
typedef vector<ii> vii;
typedef vector<vii> vvii;
typedef tuple<int,int,int> iii;
typedef set<int> si;
typedef complex<double> pnt;
typedef vector<pnt> vpnt;
typedef priority_queue<ii,vii,greater<ii> > spq;
const ll MOD=1000000007LL;
template<typename T> T gcd(T a,T b){if(a==0) return b; return gcd(b%a,a);}
template<typename T> T power(T x,T y,ll m=MOD){T ans=1;while(y>0){if(y&1LL) ans=(ans*x)%m;y>>=1LL;x=(x*x)%m;}return ans%m;}
int shift[66];
inline int getlev(int x){
int z=__builtin_clzll(x);
return 64-z;
}
inline int getmod(int x){
return (1LL<<(x-1));
}
void addshift(int x,int k){
int m=getmod(x);
if(k>=m) k%=m;
shift[x]+=k;
if(shift[x]>=m) shift[x]-=m;
if(shift[x]<0) shift[x]+=m;
}
int getorig(int V,int l){
int fval=(1LL<<(l-1)); // 2^(L-1)
int mod=getmod(l);
int P= V-fval;
int Z= fval+((P-shift[l])%mod + mod)%mod;
return Z;
}
int32_t main(){
sync;
int q; cin>>q;
while(q--){
int t,x,k;
cin>>t>>x;
int l=getlev(x);
if(t==1){
cin>>k; k%=getmod(l);
addshift(l,k);
}
else if(t==2){// propogating
cin>>k;
k%=getmod(l);
if(k<0) k+=getmod(l);
int curr=1;
for(int i=l;i<=60;i++){
addshift(i,k*curr);
curr<<=1;
}
}
else{ // printing
int P= x - (1LL<<(l-1)); // Finding index in array
int V= (1LL<<(l-1)) + ((P+shift[l])%(1LL<<(l-1)) + (1LL<<(l-1)) )%(1ll<<(l-1)); //Finding original value at the new index of X after performing the shift.
for(int i=l;i>=1;i--){
int Z = getorig(V,i); // Finding the current value
cout<<Z<<" "; // printing the current value
V>>=1; // dividing the original value by 2 to get its parent value
}
cout<<endl;
}
}
}
Tutorial is loading...
Set by : rohitranjan017
Setter's solution
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=1000005,mod=1e9+7;
vector<int> adj[M];
int par[M],lev[M];
ll v[M];
ll e[M],o[M];
ll ans,res,n;
ll powmod(ll base, ll exponent)
{
//cout<<base<<" "<<exponent<<endl;
ll ans=1;
while(exponent)
{
while(exponent%2==0)
{
base=(base*base)%mod;
exponent/=2;
}
exponent--;
ans=(ans*base)%mod;
}
return ans;
}
void dfs(int x,int depth)
{
//o[x]++;
lev[x]=depth;
int cno=0;
for(int i=0;i<adj[x].size();i++)
{
int c=adj[x][i];
if(c!=par[x])
{
par[c]=x;
dfs(c,depth+1);
if(cno>0)
{
ans=( (ans+ 2*( o[x]*e[c]%mod - e[x]*o[c]%mod + mod)%mod*v[x]%mod)+mod )%mod;
}
cno++;
o[x]+=e[c];
e[x]+=o[c];
}
}
o[x]++;
}
int main()
{
//freopen("o.out","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>v[i];
}
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1,0);
//cout<<ans<<endl;
for(int i=1;i<=n;i++)
{
//cout<<"###"<<i<<endl;
if(lev[i]%2)
{
ans=((ans+2*(o[i]*(e[1]-o[i]+1)%mod - e[i]*(o[1]-e[i])%mod +mod)%mod*v[i]%mod)%mod+mod )%mod;
}
else
{
ans=((ans+2*(o[i]*(o[1]-o[i]+1)%mod - e[i]*(e[1]-e[i])%mod +mod)%mod*v[i]%mod)%mod+mod )%mod;
}
//cout<<ans<<endl;
ans=((ans-v[i])%mod+mod)%mod;
// cout<<i<<" "<<ans<<endl;
//cout<<ans<<endl;
}
cout<<ans<<endl;
}
Tutorial is loading...
Set by : kr_abhinav
Setter's solution
#include <bits/stdc++.h>
using namespace std;
vector<map<int,int> > s;
int getedgelen(int a, int w)
{
auto it = s[a].lower_bound(w);
if(it == s[a].begin()) return 1;
it--;
return (it->second)+1;
}
int32_t main() {
ios::sync_with_stdio(false);cin.tie(0);
int n,m,a,b,w;
cin>>n>>m;
s.resize(n+1);
int ans = 0;
while(m--)
{
cin>>a>>b>>w;
int val = getedgelen(a,w);
if(getedgelen(b,w+1) > val)
continue;
s[b][w] = max(s[b][w],val);
auto it = s[b].upper_bound(w);
while(!(it==s[b].end() || it->second > val))
{
it = s[b].erase(it);
}
ans = max(ans,val);
}
cout<<ans;
return 0;
}
Tutorial is loading...
Set by : apoorv_kulsh
Setter's solution
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
const int mod = 998244353;
const int root = 15311432;
const int root_1 = 469870224;
const int root_pw = 1 << 23;
const int N = 400004;
vector<int> v[N];
ll modInv(ll a, ll mod = mod){
ll x0 = 0, x1 = 1, r0 = mod, r1 = a;
while(r1){
ll q = r0 / r1;
x0 -= q * x1; swap(x0, x1);
r0 -= q * r1; swap(r0, r1);
}
return x0 < 0 ? x0 + mod : x0;
}
void fft (vector<int> &a, bool inv) {
int n = (int) a.size();
for (int i=1, j=0; i<n; ++i) {
int bit = n >> 1;
for (; j>=bit; bit>>=1)
j -= bit;
j += bit;
if (i < j)
swap (a[i], a[j]);
}
for (int len=2; len<=n; len<<=1) {
int wlen = inv ? root_1 : root;
for (int i=len; i<root_pw; i<<=1)
wlen = int (wlen * 1ll * wlen % mod);
for (int i=0; i<n; i+=len) {
int w = 1;
for (int j=0; j<len/2; ++j) {
int u = a[i+j], v = int (a[i+j+len/2] * 1ll * w % mod);
a[i+j] = u+v < mod ? u+v : u+v-mod;
a[i+j+len/2] = u-v >= 0 ? u-v : u-v+mod;
w = int (w * 1ll * wlen % mod);
}
}
}
if(inv) {
int nrev = modInv(n, mod);
for (int i=0; i<n; ++i)
a[i] = int (a[i] * 1ll * nrev % mod);
}
}
void pro(const vector<int> &a, const vector<int> &b, vector<int> &res) {
vector<int> fa(a.begin(), a.end()), fb(b.begin(), b.end());
int n = 1;
while (n < (int) max(a.size(), b.size())) n <<= 1;
n <<= 1;
fa.resize (n), fb.resize (n);
fft(fa, false), fft (fb, false);
for (int i = 0; i < n; ++i)
fa[i] = 1LL * fa[i] * fb[i] % mod;
fft (fa, true);
res = fa;
}
int S(int n, int r) {
int nn = 1;
while(nn < n) nn <<= 1;
for(int i = 0; i < n; ++i) {
v[i].push_back(i);
v[i].push_back(1);
}
for(int i = n; i < nn; ++i) {
v[i].push_back(1);
}
for(int j = nn; j > 1; j >>= 1){
int hn = j >> 1;
for(int i = 0; i < hn; ++i){
pro(v[i], v[i + hn], v[i]);
}
}
return v[0][r];
}
int fac[N], ifac[N], inv[N];
void prencr(){
fac[0] = ifac[0] = inv[1] = 1;
for(int i = 2; i < N; ++i)
inv[i] = mod - 1LL * (mod / i) * inv[mod % i] % mod;
for(int i = 1; i < N; ++i){
fac[i] = 1LL * i * fac[i - 1] % mod;
ifac[i] = 1LL * inv[i] * ifac[i - 1] % mod;
}
}
int C(int n, int r){
return (r >= 0 && n >= r) ? (1LL * fac[n] * ifac[n - r] % mod * ifac[r] % mod) : 0;
}
int main(){
prencr();
int n, p, q;
cin >> n >> p >> q;
ll ans = C(p + q - 2, p - 1);
ans *= S(n - 1, p + q - 2);
ans %= mod;
cout << ans;
}
Tutorial is loading...
Set by : arnabsamanta
Setter's solution
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
const int N = 400004;
int n;
vector<int> e[N];
int sz[N], par[N], sp[30][N];
int V[N], L[N], CS[N];
bool mark[N];
struct tri {
long long A, B;
int C;
};
map<int, tri> nmp[N];
long long D[N]; // Sum of Distances
long long S[N]; // Sum of Depth
int T[N]; // Count
//======================================PRE-PROCESS=========================================
void getLevel(int u, int p = -1){
sp[0][u] = p;
for(auto x : e[u]) if(x != p) {
L[x] = 1 + L[u];
getLevel(x, u);
}
}
void prepAncestor(){
for(int i = 1; (1 << i) <= n; ++i) {
for(int j = 1; j <= n; ++j) {
sp[i][j] = sp[i - 1][sp[i - 1][j]];
}
}
}
int dist(int u, int v){
if(L[u] < L[v]) swap(u, v);
int lgn = 0;
while((1 << lgn) < n) lgn++;
int ans = 0;
for(int i = lgn; i >= 0; --i){
if(L[u] - (1 << i) >= L[v]){
u = sp[i][u];
ans += (1 << i);
}
}
if(u == v) return ans;
for(int i = lgn; i >= 0; --i){
if(sp[i][u] != sp[i][v]){
ans += 1 << (i + 1);
u = sp[i][u];
v = sp[i][v];
}
}
return ans + 2;
}
//=================================CENTROID DECOMPOSITION===================================
void getSize(int u, int p = -1) {
sz[u] = 1;
for(auto v : e[u]) if(v != p && !mark[v]) {
getSize(v, u);
sz[u] += sz[v];
}
}
int getCentroid(int u, int p, int lim) {
for(auto v : e[u]) if(v != p && !mark[v] && sz[v] > lim) {
return getCentroid(v, u, lim);
}
return u;
}
void decompose(int u, int p = -1) {
getSize(u);
int cen = getCentroid(u, -1, sz[u] / 2);
par[cen] = p == -1 ? cen : p;
mark[cen] = true;
for(auto v : e[cen]) if(v != p && !mark[v]) {
decompose(v, cen);
}
}
//==========================================QUERY-HANDLER===============================================
void updAns(int u, int add) {
int Z = V[u];
tri tY = nmp[u][Z];
ll ret = tY.A;
int y = u, x = par[u];
while(y != x) {
tri tX = nmp[x][Z];
ret += 1LL * (tX.C - tY.C) * dist(x, u) + (tX.A - tY.B);
y = x;
tY = tX;
x = par[x];
}
ret <<= 1;
int mul = add ? 1 : -1;
D[Z] += mul * ret;
S[Z] += mul * L[u];
T[Z] += mul;
}
void updTree(int u, bool add) {
int Z = V[u];
int mul = add ? 1 : -1;
for(int x = u; ; x = par[x]) {
tri &tX = nmp[x][Z];
tX.C += mul;
if(!tX.C) {
nmp[x].erase(Z);
} else {
tX.A += mul * dist(u, x);
tX.B += mul * dist(u, par[x]);
}
if(x == par[x]) break;
}
}
void upd(int u, bool add) {
if(add) {
updTree(u, add);
updAns(u, add);
} else {
updAns(u, add);
updTree(u, add);
}
}
//=========================================MAIN============================================
int main(){
int m, q, ac;
scanf("%d %d %d %d", &n, &m, &q, &ac);
for(int i = 1; i <= n; ++i) {
scanf("%d", &V[i]);
}
for(int i = 2; i <= n; ++i) {
int v;
scanf("%d", &v);
e[v].pb(i);
e[i].pb(v);
}
for(int i = 1; i <= m; ++i) {
scanf("%d", &CS[i]);
}
L[1] = 1;
getLevel(1);
prepAncestor();
decompose(1);
for(int i = 1; i <= n; ++i) {
upd(i, true);
}
while(q--) {
int t;
scanf("%d", &t);
if(t == 1) {
int u, v;
scanf("%d %d", &u, &v);
upd(u, false);
V[u] = v;
upd(u, true);
}
else if(t == 2) {
int v;
scanf("%d", &v);
long double ans = S[v] * T[v] - D[v] / 2;
ans *= 1LL * CS[v] * CS[v];
ans += 1LL * n * ac * ac;
long long anst = 2LL * CS[v] * ac * S[v];
ans -= anst;
cout << fixed << setprecision(12) << ans / n << "\n";
}
}
}
Do give your feedback here : https://goo.gl/forms/xbsdMxnkA3XsG4092. Would love to hear your feedback, since that would help us get better!










Auto comment: topic has been updated by apoorv_kulsh (previous revision, new revision, compare).
Auto comment: topic has been updated by apoorv_kulsh (previous revision, new revision, compare).
Really good problem set.
and solves nothing
hahahahahahahahahahahahahahahahahahahahahahahahahahahahahahahaha
Solution for C is suboptimal, you can greedily choose the greatest K such that 2^K-1 <= X.
The array should have exactly X subsequences.
Yes, and?
You don't need to output an array with minimum number of elements. You just need to find any array with size ≤ 104. There may be a different solution than described here, which is able to produce an array with lesser number of elements and satisfying the constraints.
For problem F, I created another graph with edges as vertices and then ran DFS on it. My solution is exceeding memory limit and I couldn't optimize it furthur. Please help. http://codeforces.com/contest/960/submission/37094773
At the bottom of your submission there is the part of the test your solution got MLE. As you will notice, the test contains 1e5 self loops. The problem is that for such a graph, by turning edges to nodes, you make new graph with |E|2 edges, thus your algo total complexity is |E|2 which is too much and the memory you take then is |E|2 too, which caused MLE before TLE :<.
edit: notice that the problem still exists in usual graphs without self-loops. That's why switching vertices with edges is possible only if every vertex has small degree, cause every vertex causes his adjacent edges to form a clique, when you transform the graph
Can someone explain to me how to write Dynamic Segment Tree in O(n*log n)? Is it possible to do it iteratively? Thank you in advance!
I usually do segment tree recursively. The way you use this structure is the same, but, instead of creating all nodes, you just create nodes that you actually need (you do not need a build function, only update).
Suppose that you will insert/update something on index 5 and left node keep values in [0, 5], there is no need to worry about right node.
It's kinda of more complex, but you can do this with lazy propagation too.
My submission on F: 37069514
Thank you :)
sorry if I am asking for too much but can this also be implemented simply using STL's map ?
If yes , can you show a sample code?
That is what i have done before asking my question. However using STL`s map you will get O(n*logn^2). Due to this (probably) i got TLE on test 12. Here is my code. 37099586
Check out setter's solution tab for maps + O(nlogn) solution :)
Also check out submission 37130983 based on dynamic segment tree approach
For F my O(n) soln is giving TLE http://codeforces.com/contest/960/submission/37123425 can anyone help please
Video solution to Problem B: https://youtu.be/s_qtv8MisbQ?t=3m13s
960B - Minimize the error
Divide by Zero 2018 and Codeforces Round 474 (Div. 1 + Div. 2, combined)
Amazing problemset. Although in my opinion, problem F is much easier to write than problem E :)
We apologise for the scoring issue. We underestimated/overestimated a few problems.
Glad to hear you like the problem set :)
For F my O(n) soln is giving TLE http://codeforces.com/contest/960/submission/37123425 can anyone help please
In F your solution is quadratic in the worst case, when all the edges are between the same two nodes. Check the case you got tle on
got it,thanks
Can someone please tell me why I got tle in question F Link to my code http://codeforces.com/contest/960/submission/37079088
maybe you are making same mistake as i did..read reply on my comment above
Why dynamic segment tree is required in problem F? Can't it be solved with static segment tree? Can anyone help me where I am going wrong?
Sorry for my poor English: It is possible solve it with static segment tree: For every edge that goes from node u to node v add this in a list of edges that leave the node u, then in every node the edges are ordered, because you add this in the same order of the input and in every node have a segment tree of max, that store the max length of a path that end in this edge, it is easy to see that the sum of all edges for every node is M, because every edge is added to only one node, then initially the length of all the path for every edge is 1, in other list that contains all the edges sorted by minimum weight process the edges now, what happen when a edge (u, v, w) comes, it is possible to traverse along this, then update in node v all the edges that comes after the current edge in the input with x=value of this+1 we obtain this value doing a query to the segment tree in node u for the position of the current edge, the position (p) of the first edge that comes after the current edge is possible search it by a binary search in the list of edges of node v, then update the range (p, end) with x, every time that you process one edge update the answer, only left one problem: what happen when a edge of weight w update other after(in the input) with the same value w, this is violating that the weights of the path is strictly increasing, to solve this, store the value of all the next edges to process of the same weight w, used this value to update, so not matter that you update "invalid" edges weight lower or equal to the current because this values never will by used when you process the edges sort by weight Finally let you a link to my solution: 37110519 It is possible solve with a unique segment tree you only assign for every edge in the same node a continuous position on it.
Nice editorial especially problem D
HDU4372 960G - Bandit Blues
In problem G, how did you do FFT by modulo? Can you explain it more detailed? I know that it is because MOD-1 is divisible by 2^23, but what it gives to us? And where did you get numbers root and root_1?
This is in fact [number theoretic transform](https://en.m.wikipedia.org/wiki/Discrete_Fourier_transform_(general)#Number-theoretic_transform).
Root is a 223-th primitive root, and root_1 is perhaps its inverse. How to find it? We don't really know. Luckily, if r is a primitive root modulo n, and gcd(e, n - 1) = 1, then re is also a primitive root. So you can just find it using brute force.
For problem G, is there some intuitive way to realize that number of permutations with
|LIS| = kk elements visible from front is in fact just Stirling numbers of first kind? (It is evident from the recurrence, but not able to create a mapping between the two)We can solve the problem as follows:
For each i from 0 to n, find the number of ways we can permute i elements to have exactly a - 1 records lets call it f(i, a - 1). In the end , we can select f(i, a - 1), f(n - 1 - i, b - 1), and we place n between them to make it exactly equal to (a, b) records.
We can find that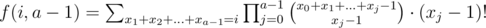 using basic combinatorical interpretations.
using basic combinatorical interpretations.
Now, also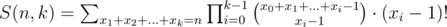 .
.
So, f(i, a - 1) = S(i, a - 1).
Now, to find final answer you can use the formula mentioned in the editorial, and here
Thanks, but that's not what I asked. I already know that their recursion formulas (and polynomial form) are identical.
What I'm looking for is an intuitive explanation which tells why is the number of permutations with exactly k cycles (i.e Stirling numbers of first kind) equal to the number of permutations with
|LIS| =k elements visible from front. Is there some explanation which is able to map number of cycles to number of elements visible from front?On an unrelated note, can you elaborate on "using basic combinatorical interpretations." please? How do you come up with that formula?
We can build each permutation of n elements having k records as follows :
Express n as sum of k positive integers, x1, x2, ...xk. Now, repeat k times :
Append this block to the left of the previous block.
The number of ways to select elements for the ith block corresponds to the ith binomial coefficient in the product, and the factorials for internal permutations.
We iterate over all ways to express n as a sum like this.
Nice!
This explanation also helps realize the equivalence between number of cycles and
size of LISnumber of elements visible from front.x1, x2, .. xk can correspond to the size of the K cycles. The largest element of each cycle corresponds to an LIS element.