The objective of this post is NOT understanding FFT or Karatsuba, or any algorithm that performs fast convolutions, it's about understanding one of its uses
Hi Codeforces community! I wanted to write this blog entry to help coders who would like to see a nice example of convolutions used in a problem which, at first sight, has little to no relation with polynomial multiplication (of course it has, it's a convolution after all)
The problem is as follows: You are given two strings S and P, with lengths n and m respectively, where m ≤ n
For each substring T of S with length m, we have to find the one that maximizes the number of positions with the same character, i. e T[i] = P[i]
For the sake of simplicity, let us assume that our strings consists only of letters a and b. For example, if S = baabab and P = bba, let's calculate the "similarity" between P and each substring of S of length 3.
s(baa, bba) = 2
s(aab, bba) = 0
s(aba, bba) = 2
s(bab, bba) = 1
We can see that there are two substrings which maximize the similarity (any answer will be fine)
A naive approach has a O(n·m) time complexity and uses O(n + m) memory
This should be OK if 1 ≤ n, m ≤ 1000. What about 1 ≤ n, m ≤ 105? We have to find a faster way to apply  for every substring T of S
for every substring T of S
First, let's try to change the formula above with a more mathematical approach. If we map each character {a,b}={0,1}, we can apply the next formula:
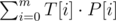 . This will give us the number of 1's (originally, b's) that match.
. This will give us the number of 1's (originally, b's) that match.
Let Sc be the complement of S (0 becomes 1, and viceversa). To compute the number of 0's that match, we apply
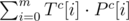
Now what? This doesn't improve the complexity at all
Let's remember how the convolution f of two discrete functions g and h is defined:
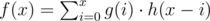
Now we're talking! This looks pretty similar to the formulas previously explained.
Next we will try to change our formulas to a simple convolution. First we will say that our array S and P are two functions g and h whose domain is [0, n - 1] and range is {0,1}.
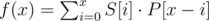
But the formula is incorrect, this convolution, for each x applies the similarity formula, but reversing P!
This is our first issue, which we can easily solve by reversing P ourselves. Let's call Pr the reversed version of P. We can see that
 is equivalent to
is equivalent to 
Our second issue is, m ≤ n. We can easily solve this issue (again) by adding some trailing zerores to Pr, which is equivalent to add leading zeroes to P until m = n
But, what is f(x) exactly, and how can this help us to improve the time complexity?
We saw that  , which is the same as taking a preffix of S and (this is the tricky part) a suffix of P, each of length x + 1
, which is the same as taking a preffix of S and (this is the tricky part) a suffix of P, each of length x + 1
If we take x = m - 1, we can see that this applies the similarity function to the whole pattern P and the first substring of S which starts at 0. If we take x > m - 1 then we apply the function to P and the (x - m + 1) - th substring of S. And if we take x < m - 1 we apply the function to a substring which goes out of the bounds of S.
Let's check our example S = baabab and P = bba. First, let's map each character S = 100101 and P = 110.
Then,Pr = 011 and let's add some trailing zeroes: Pr = 011000.
Let's calculate the convolution f
f(0) = 0
f(1) = 1
f(2) = 1
f(3) = 0
f(4) = 1
f(5) = 1
Great! f computes the number of 1's that match. What about the number of 0's? Let's apply the same procedure to Sc and Pc
Sc = 011010 and Pc = 001
Prc = 100000
fc(0) = 0
fc(1) = 1
fc(2) = 1
fc(3) = 0
fc(4) = 1
fc(5) = 0
Fine! Now, the answer should be max f(i) + fc(i) where i is in [m - 1, n - 1]
With this approach, we can solve the problem with a O(nlogn) time complexity using an algorithm like FFT to perform the convolution, or maybe Karatsuba algorithm
And what if the alphabet size is not 2?
For each character on the alphabet, we apply the convolution. Suppose fai is the convolution between S and P where, if S[i] = = ai then S[i] = 1, else S[i] = 0 (the same applies for P), for every character ai on the alphabet a
The answer should be max 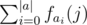 with j in [m - 1, n - 1]
with j in [m - 1, n - 1]
This solution has a O(|a|·nlogn) time complexity, where |a| is the size of the alphabet
And what now?
Here are some problems which can be solved using this approach
Hope you like this post, and helps you solving some convolution problems!










Auto comment: topic has been updated by snacache (previous revision, new revision, compare).
Thank you for this nice article, i really like convolution problems :)
Anyway, the paragraph that explains when the alphabet is not 2, i think it should be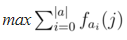 with j [m-1,n-1] without the complement part, since we are summing over all the alphabet.
with j [m-1,n-1] without the complement part, since we are summing over all the alphabet.
You're totally right! Thanks, fixed!
Great!
Thank you for this article! I've seen a lot of string matching problems for which the solution was to utilize some sort of convolution, and I had no idea where that came in and how it applied. This cleared a lot of things for me. Thanks again!