Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
| Name |
|---|



Solution of G with maxflow idea.
http://codeforces.com/contest/978/submission/38193150
Nice!
I also solve it with maxflow like an assignment problem. 38199894
What's the time complexity of your solution?
doesn't matter dude! his sol is over-kill for this problem. just assign days greedily. Whichever exam comes first gets preparation day first.
Very fast! Thank you
Thanks for quick explanation. Is there any solution which works faster than "brute solution" for problem D?
Faster than O(n)? I think, no.
For G you don't need to iterate all the exams every day.
38195700 complexity is O(n*logm) insted of O(n*m)
Excellent thanks for posting
I might be a little late but can you please explain your logic ?
A simple way of understanding 978E - Bus Video System:
Define pre[i] =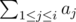
Let's take an arbitrary variable initial which could hold all possible initial values.
It is easy to see this inequality holds true:
0 ≤ initial + pre[i] ≤ w,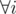
Which implies:
- pre[i] ≤ initial ≤ w - pre[i]
We can reduce this to:
max(0, - pre[i]) ≤ initial ≤ min(w, w - pre[i])
Solving this inequality and finding the range gives us the final answer.
For F instead of using vectors with quarrels another nice way is to process the quarrels by incrementing an array containing the "number of quarrels with less skilled programmers". Then we can just directly subtract the number in that array at the end.
My solution 38178463 to problem 978E - Bus Video System is O(n).
My solution 38166452 to problem 978B - File Name was similar to the one in the tutorial, but easiest, it's how many ocurrences have the string "xxx" in the string s.
fcspartakm I think there was a typo in the tutorial of problem F: "we can user array of pairs" for "we can use array of pairs".
Regexp solution is very easy to write for B :P