Задача A (div2) — Шкафы
Автор: max777alex
В этой задаче можно рассмотреть независимо все левые дверцы шкафов и, аналогично, все правые. Очевидно, чтобы привести все левые дверцы шкафов в одинаковое положение, нужно определить какое из двух состояний ("левая дверца открыта" или "левая дверца закрыта") встречается чаще. Все левые дверцы, которые находятся в другом состоянии требуется привести к этому. Аналогично надо поступить и с правыми дверцами. Если аккуратно посчитать в таком случае количество операций изменения состояния дверцы, то это оно и будет ответом.
Задача B (div2) — Котенок Гав
Авторы: max777alex, pkhaustov
В данной задаче требовалось найти минимальное положительное N-значное число, которое делится без остатка на 2, 3, 5 и 7. Очевидно, раз все эти четыре числа являются простыми, то число, которое делится на все эти четыре числа, должно делиться на их произведение 2·3·5·7 = 210. Для N < 3 такого числа не существует. Для N = 3, конечно же, ответ равен 210. Для N > 3 следуем следующему алгоритму.
Найдем остаток R от деления 10N - 1 на 210. Далее требуется добавить 210 - R к 10N - 1, чтобы получилось число, кратное 210. Учитывая, что 0 ≤ R < 210, получаем, что последние три разряда числа определяются значением R, а оставшиеся разряды — совпадают с соответствующими разрядами числа 10N - 1.
Можно также было заметить закономерность для последних трех разрядов с изменением N и заменить вычисления остатков аккуратным разбором случаев.
Задача A (Div1), C (div2) — Электроник-футболист
Авторы: am-real
Для начала временно избавимся от радиуса мяча — сдвинем верхнюю стену на радиус вниз. Мяч, в таком случае, можно считать материальной точкой. Штанги не трогаем. Отразим центр мяча относительно сдвинутой верхней стены. Соединим полученный отраженный центр мяча и точку (0, y1 + r).
Далее остается аккуратно определить, не касается ли мяч левой стены. Очевидно, что точкой стены, наиболее близко лежащей к траектории центра мяча, будет штанга (0, y2). Таким образом достаточно проверить расстояние от этой точки до траектории мяча. Если оно меньше радиуса, значит ответа нет, иначе — точка пересечения проведенной ранее линии и сдвинутой на радиус вниз стеной и будет ответом.
Если целиться выше точки (0, y1 + r), траектория центра мяча только приблизится к штанге (0, y2), поэтому целиться в другие точки смысла не имеет.
Задача B (Div1), D (div2) — Конфеты — каждому!
Автор: pkhaustov
В задаче предполагалось, что друзья из Простоквашино могут закончить свой путь на любом участке улицы. Давайте изначально предположим, что заканчивать свой маршрут друзьям можно только на последнем участке улицы. В таком случае решение более, чем очевидно.
С ростом количества изначально имеющихся с собой конфет, время, которое требуется для угощения всех жителей может либо не изменяться, либо уменьшаться. Следовательно, здесь применим бинарный поиск по количеству конфет. С помощью бинарного поиска закрепим количество конфет, которые мы изначально взяли с собой. Идем слева направо (от первого участка, до последнего). Если находимся на участке с магазином — обязательно покупаем конфеты (денег у нас бесконечно много, значит, нет смысла не покупать конфеты). Если мы находимся на участке с домом, то при наличии конфет — угощаем жителей этого дома. Если же конфет у нас нет, то пропускам этот дом. Несложно доказать, что возвращаться назад выгодно только тогда, когда у нас достаточно конфет, чтобы угостить жителей всех пропущенных домов. Пусть первый пропущенный дом оказался на участке L. На участке R мы купили конфеты, и теперь их достаточно, чтобы угостить жителей всех пропущенных домов. Тогда участок от L до R мы дополнительно пройдем еще на два раза. Если попытаться угостить жителей пропущенных домов раньше, чем мы достигнем участка R (на участке T), то участок от L до T нам так же придется преодолеть дополнительно на два раза. Однако, так как мы не можем угостить всех жителей на отрезке от L до T, это говорит о том, что придется преодолеть некоторую часть этого интервала еще два раза, для чего нам еще на два раза придется преодолеть отрезок от T + 1 до R. Очевидно, что преодолев на два раза отрезки (L, T) и (T + 1, R) мы, фактически, преодолели на два раза отрезок от L до R. Помимо этого, какую-то часть отрезка от L до T нам потребуется преодолеть еще два раза. Получается, что количество времени, которое нам потребуется, будет строго больше, чем в первом случае. Аккуратно моделируем процесс за O(N), чтобы определить минимальное количество времени, которое потребуется на выполнение прохода по улице.
Теперь предложим модификацию для случая, когда закончить свое путешествие друзья могут на любом участке. В таком случае некоторую часть P улицы вовсе не обязательно посещать. Такая часть улицы представляет собой несколько (возможно ноль) последних участков этой улицы и не содержит домов. Определить такую часть можно за O(N) для каждого имеющегося изначально количества конфет на руках у друзей. Назовем улицу за вычетом ее части P полезной частью. В какой-то момент времени может оказаться так, что выгоднее дойти до конца полезной части и пойти обратно до тех пор, пока жители всех пропущенных домов не получат свои конфеты, после чего раздача сладостей прекращается. Такую проверку можно осуществлять за O(1) на каждом шаге вышеописанного решения.
Результирующая асимптотика O(N·logN) (логарифм возникает из-за использования бинарного поиска).
Задача C (Div1), E (div2) — День рождения ослика Иа-Иа
Сформулируем ряд утверждений, которые помогут нам решить задачу. При любом действии Винни-Пуха количество нетронутых горшков на любой из полок не может быть увеличено. Таким образом, если на полке с номером i изначально находилось Ai горшков, то в любой момент времени нетронутых горшков на этой полке будет C, причем 0 ≤ C ≤ Ai. Несложно поддерживать вероятность P(i, C) того, что на полке с номером i находится C нетронутых горшков для всех возможных значений i и C. Это можно сделать с помощью динамического программирования.
Очевидно, ответом после каждой операции будет сумма P(i, 0) по всем возможным значениям i. Заметим, что после каждой операции число нетронутых горшков может измениться только на полке, с которой Винни-Пух берет горшки. Формулы для переходов между состояниями динамического программирования достаточно тривиальны. Какие-то трудности могут возникнуть при выводе формул для ki ≠ 1. Этих трудностей можно избежать, если разбивать запросы с ki ≠ 1 на ki запросов с ki = 1, ведь 1 ≤ ki ≤ 5, и, следовательно, время выполнения существенно увеличено не будет. Допустим и вариант, когда запросы не разбиваются. Для этого требуется аккуратно вывести несложные формулы переходов.
Несложно заметить, что перед первым запросом можно посчитать сумму P(i, 0) по всем значениям i. Далее, при выполнении каждого запроса ui, vi, ki, до его выполнения отнимать P(ui, 0) от ответа, а после его выполнения — добавлять новое значение P(ui, 0) к ответу.
Если обозначить наибольшее значение Ai по всем i, как MaxA, то асимптотика такого решения, очевидно, будет O(N·MaxA). Памяти такое решение так же требует O(N·MaxA).
Задача D (Div1) — Ежик и звезды
Для начала заметим, что задачу можно свести к более простому варианту аналогичной задачи. В первую очередь, можно избавиться от точек, которые не находятся между двумя заданными во входных данных лучами, выходящими из начала координат. После чего можно повернуть все точки относительно начала координат на такой угол, чтобы один из лучей совпал с одной из осей координат. Для определенности положим, что мы повернули все точки на угол α1 так, чтобы луч, который был пущен под этим углом совпал с осью OX.
Теперь задача существенно упрощается. Все точки лежат в первой координатной четверти (то есть все координаты строго положительны), и имеется прямая L0 под углом α2 - α1, которая проходит через начало координат и все точки лежат ниже нее. Добавим точку начала координат в наш набор, как фиктивную. Проведем через каждую из точек прямую Li параллельную прямой L0. Отсортируем точки в порядке убывания ординаты пересечения прямой Li с осью Oy. Пойдем с конца. Для каждой точки i будем считать длину наибольшей цепочки MaxL(i), которая начинается из этой точки (смотреть будем на те точки, которые уже рассмотрены в нашем обратном порядке обхода). Для каждой точки i мы будем рассматривать все точки j между заданными лучами и выбирать такую, что MaxL(j) максимально, после чего полагать MaxL(i) = MaxL(j) + 1.
Чтобы рассмотреть только те точки, которые находятся в области между лучами выходящими из точки i, требуется выбрать такие точки j, для которых Li пересекает ось Oy выше, чем Lj, и ордината Yj не меньше, чем ордината Yi. Заметим, что из-за порядка сортировки первое условие всегда выполняется, если аккуратно обработать точки с одинаковыми прямыми Li. Для соблюдения оставшегося ограничения достаточно воспользоваться стандартной идеей с деревом интервалов. Но гораздо лучше заметить, что эта задача эквивалентна задаче нахождения поиска наибольшей возрастающей последовательности. Ответом будет значение MaxL для фиктивной точки начала координат.
Как результат, имеем решение с асимптотикой O(N·logN) и O(N) затратами памяти.
Задача E (Div1) — Бесконечная матрица
Автор: pkhaustov
Несложно заметить ряд закономерностей. Для начала обратим внимание на первую строку матрицы. В i-ом столбце первой строки находится элемент со значением (i - 1)2 + 1. Несложно найти закономерность для первого столбца — там в чистом виде квадраты натуральных чисел. Диагональ тоже задается легкой закономерностью i2 - i + 1.
Дальше несложно заметить, что в любом столбце до элемента главной диагонали значения увеличиваются с шагом в единицу. После элемента главной диагонали элемент в i-ой строке равен i2 - i + 1. Как видим, можно и диагональный элемент отнести к этой же закономерности.
Для подматрицы, в которой нужно найти сумму, выполняем разбиение на участки над главной диагональю и под ней и производим вычисления согласно приведенным закономерностям. В авторском решении использовались суммы для квадратов первых N чисел, для суммы сумм квадратов первых N чисел и (выраженная через них) сумма кубов первых N чисел. Существуют и другие варианты формул.
Теперь стоит выполнить все вычисления по модулю 1010. Для того, чтобы отследить, имеет ли число более десяти знаков, будем хранить (помимо остатка) частное от деления на 1010 по модулю нескольких различных простых чисел порядка 109. На практике достаточно и одного простого числа, но для генерации тестов использовалось сразу четыре.
Для решения задачи также можно использовать и типы данных, связанные с длинной арифметикой. Много решений с такой реализацией проходили. Однако, стоит отметить, что нельзя погарантировать хорошее быстродействие такому решению.











There is a slightly different solution of D: you can change basis with : replace coordinates (x, y) with (x·c - y·d, y·b - x·a). You can treat it like 'oriented distances' to the lines.
: replace coordinates (x, y) with (x·c - y·d, y·b - x·a). You can treat it like 'oriented distances' to the lines.
Now we have a1 = 0 and a2 = 90 and this is standard DP problem, which can be solved in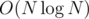
You can also see my code: 2646289. It's pretty straightforward
Same problem and same solution I've seen in All-Ukrainian Olympiad of Informatics. Problem (F).There is also a tutorial for this problem on CF, but only in Russian.
Also somewhat harder version of problem E was proposed on Topcoder.
Harder? I don't think so. Here solution is quite trivial. We've dicussed it before the contest with Seyaua and we've found a lot of differences between this two problems.
solution is quite trivial. We've dicussed it before the contest with Seyaua and we've found a lot of differences between this two problems.
Oh, come on. I can assure you that it was not the hard idea which stopped people from solving problem E from your contest.
Just for your notice: it wasn't necessary to derive all the formulas by hand. One could use Maple/Wolfram Mathematics/Matlab/whatever else to perform polynomial interpolation and then just add up these 3 polynomials to get the answer. The problem was in this part of statement which asked to output only the last 10 digits. Why didn't one ask to output 17 digits or even the last 10 digits of panswer? Both of these cases are also solvable, but take even more time than the original problem. I believe that all solutions that didn't pass final tests either got TL or just had some error related to the output format. Was it intended?
Well, it wasn't intended, but I did realize that this part of the problem could be the tough one. I've noticed that output modulo some number is quite boring, so I've decided to complicate this problem a little. The cost of this problem corresponds to the risks that this problem brings.