_QWOiNYUIVMPFSBKLiGSMAP_'s blog

Primitive roots
By _QWOiNYUIVMPFSBKLiGSMAP_, history, 5 years ago, In English

Could anyone explain to me the proof for such a method of checking whether a number is primitive root or not http://zobayer.blogspot.com/2010/02/primitive-root.html

why should i check only certain numbers to be equal to one or not ?

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Since n is a prime, we know that gφ(n) = gn - 1 = 1. We want to know if there is another exponent e < n - 1 such that ge = 1.

Let e be the smallest, positive integer with ge = 1. This means that the exponents that give 1 are exactly 0, e, 2e, 3e, .... This means that e divides n - 1. If e is really smaller than n - 1, then there must exist a prime factor p of n - 1, such that e still divides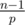 . Which means that .

So it is sufficient to check if any of the terms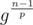 , with p prime and p | n - 1, is equal to 1.

→ Reply