Hi,
Let's say I have a set of lines, y = ax+b and three types of online queries:
- Given a and b, insert the line.
- Given a and b, delete the line (it is assured that the line exists)
- Given x0, print the maximum possible value of y.
(a is distinct for all the lines, a & b are integers.)
number of lines <= 1e5.
number of queries <= 3e5.
So O(log n / log^2 n / sqrt n) should work, according to me.
Can anyone help me with this?











If it's offline it's doable with LiChao segment tree in MlogMlog(Xmax * eps) about the same way you do dynamic connectivity: you support only insert operations on certain segments of activity (every segment is active from the moment it was inserted to the moment it got erased/the operations ended). Using LiChao segment trees you can also "take back" operations in logN (which can't be done with usual dynamic CHT).
I'm not aware of any solution for the online version of this problem, although I have thought about that intensively.
Can you provide a link to read about LiChao segmant tree.
Thanks.
Here you can find a nice tutorial for LiChao Segment trees.
As for the dynamic connectivity, you can learn more about it here and in the comments of the blog.
Your can also use normal incremental CHT: If you store one data structure per recursion level and apply the updates to the one on the current level, the undo operation can be done by clearing the one on the current level. At the leaves, you query all data structures (at most ) and take the maximum. This takes
) and take the maximum. This takes 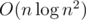 time in total. If you presort all updates and queries by x-coordinate, the linear-time data structure for monotone coordinates and queries that uses a deque instead of a set can be used, this achieves
time in total. If you presort all updates and queries by x-coordinate, the linear-time data structure for monotone coordinates and queries that uses a deque instead of a set can be used, this achieves  time overall.
time overall.
For the online version, switch to a dual space where the problem is
To solve this, build a segment-tree (you might need one based on a BST for bigger coordinates) over the points sorted by x-coordinate where each node stores the upper convex hull in a persistent BST. When merging two nodes, we need to find the upper tangent of the convex hulls (as in the divide&conquer algorithm for convex hull), split the BSTs at the points where the tangents touch and join them. This can be done in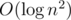 by nesting two binary searches (one on the left and one on the right). Deletions and insertions are handled by the BST + recomputation along the insertion path by merging, they take
by nesting two binary searches (one on the left and one on the right). Deletions and insertions are handled by the BST + recomputation along the insertion path by merging, they take 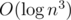 each.
each.
To query, do a ternary search on the BST stored at the root. This will take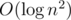 time naively and can be sped up to
time naively and can be sped up to  if we each node stores it's successor in the persistent BST. The total memory consumption can be reduced to
if we each node stores it's successor in the persistent BST. The total memory consumption can be reduced to  if each node reuses the same
if each node reuses the same  nodes for each merge done at it.
nodes for each merge done at it.
The time for merging two upper hulls can be reduced to by a bunch of case-distinctions, see slides 20 — 30 here. This reduces the insertion and deletion time to
by a bunch of case-distinctions, see slides 20 — 30 here. This reduces the insertion and deletion time to 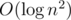 .
.
Finally, there's also an online solution with amortized time per insertion or deletion, see 'Dynamic Planar Convex Hull' by 'Riko Jacob', if you want to read 129 pages (I didn't).
time per insertion or deletion, see 'Dynamic Planar Convex Hull' by 'Riko Jacob', if you want to read 129 pages (I didn't).
Can you explain in more detail your offline solution?
Dynamic connectivity + dynamic convex hull you can achieve O(n * log2(n)).
Also sqrt(n) blocks, rebuild requiring block for updates, query each block and you can achieve O(n * sqrt(n) * log(n)).
Can you elaborate on how to do it using Dynamic connectivity + dynamic convex hull?
If you know what that mean, it's not a interesting solution. The main goal of connectivity is to get rid of delete updates.
Doesn't work: when using dynamic CHT, you can't take back operations (because it has amortized complexity, not even if you use persistent BSTs) and you need that for dynamic connectivity.
As for the second approach: it also works for online operations and its real complexity is sqrt (NlogN) which is not that bad (you an choose this as appropriate block size K and do update in O(K) and query in O(N/KlogN) as you can skip a logN when rebuilding, because you already have the list of lines sorted by their slope).
Okay, you are right about both parts.
Second approach: O(n sqrt n), build for each sqrt block and no consider erase query nodes, in the first build you should sort the array, but not in the last builds, you only sort sqrt nodes and merge.
Problem from ongoing contest
It is, but the contest problem is a little more specific with remove operations and easiest solution to code is different.
Can someone provide any good tutorial link on convex hull trick.
https://wcipeg.com/wiki/Convex_hull_trick
https://e-maxx-eng.appspot.com/geometry/convex_hull_trick.html