Tutorial
Tutorial is loading...
Solution (Vovuh)
n, m = map(int, input().split())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
pos = 0
for i in a:
pos += (pos < len(b) and b[pos] >= i)
print(pos)
1009B - Minimum Ternary String
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
string s;
cin >> s;
string ans;
int cnt = 0;
for (auto c : s) {
if (c == '1') ++cnt;
else ans += c;
}
int n = ans.size();
int pos = -1;
while (pos + 1 < n && ans[pos + 1] == '0') ++pos;
ans.insert(pos + 1, string(cnt, '1'));
cout << ans << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
typedef long long li;
int main() {
int n, m;
scanf("%d%d", &n, &m);
li neg = ((n - 1) / 2) * li((n - 1) / 2 + 1);
if (n % 2 == 0) neg += n / 2;
li pos = n * li(n - 1) / 2;
li ans = 0;
forn(i, m){
int x, d;
scanf("%d%d", &x, &d);
ans += x * li(n);
if (d < 0)
ans += neg * d;
else
ans += pos * d;
}
printf("%.15f\n", double(ans) / n);
return 0;
}
1009D - Relatively Prime Graph
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 100000;
pair<int, int> ans[N];
int main() {
int n, m;
scanf("%d%d", &n, &m);
if (m < n - 1) {
puts("Impossible");
return 0;
}
int cur = 0;
forn(i, n) for (int j = i + 1; j < n; ++j){
if (cur == m)
break;
if (__gcd(i + 1, j + 1) == 1)
ans[cur++] = make_pair(j, i);
}
if (cur != m){
puts("Impossible");
return 0;
}
puts("Possible");
forn(i, m)
printf("%d %d\n", ans[i].first + 1, ans[i].second + 1);
return 0;
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#include<bits/stdc++.h>
using namespace std;
const int MOD = 998244353;
int add(int x, int y)
{
x += y;
while(x >= MOD)
x -= MOD;
while(x < 0)
x += MOD;
return x;
}
int mul(int x, int y)
{
return (x * 1ll * y) % MOD;
}
int main()
{
int n;
scanf("%d", &n);
vector<int> a(n);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
int ans = 0;
vector<int> pw2(1, 1);
while(pw2.size() < n)
pw2.push_back(mul(pw2.back(), 2));
int cur = mul(pw2[n - 1], a[0]);
for(int i = 0; i < n; i++)
{
ans = add(ans, cur);
if(i < n - 1)
{
cur = add(cur, -mul(pw2[n - 2 - i], a[i]));
cur = add(cur, mul(pw2[n - 2 - i], a[i + 1]));
}
}
printf("%d\n", ans);
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#define _CRT_SECURE_NO_WARNINGS
#include <vector>
#include <cstdio>
#include <iostream>
#include <algorithm>
// RJ? No, thanks
using namespace std;
const int N = 1000043;
struct state
{
vector<int>* a;
int cur_max;
int sz()
{
return a->size();
}
void add(int i, int val)
{
(*a)[i] += val;
if(make_pair((*a)[i], i) > make_pair((*a)[cur_max], cur_max))
cur_max = i;
}
};
state pull(state z)
{
if(z.sz() == 0)
{
state c;
c.a = new vector<int>(1, 1);
c.cur_max = 0;
return c;
}
else
{
state c;
c.a = z.a;
c.cur_max = z.cur_max;
c.a->push_back(0);
c.add(c.sz() - 1, 1);
return c;
}
}
state merge(state a, state b)
{
if(a.sz() < b.sz())
swap(a, b);
state c;
c.a = a.a;
c.cur_max = a.cur_max;
int as = c.sz();
int bs = b.sz();
for(int i = 0; i < bs; i++)
a.add(as - i - 1, (*(b.a))[bs - i - 1]);
return a;
}
state s[N];
int ans[N];
vector<int> g[N];
void dfs(int x, int p = -1)
{
s[x].a = new vector<int>(0);
s[x].cur_max = 0;
for(auto y : g[x])
if(y != p)
{
dfs(y, x);
s[x] = merge(s[x], s[y]);
}
s[x] = pull(s[x]);
ans[x] = s[x].sz() - s[x].cur_max - 1;
}
int main()
{
int n;
scanf("%d", &n);
for(int i = 0; i < n - 1; i++)
{
int x, y;
scanf("%d %d", &x, &y);
--x;
--y;
g[x].push_back(y);
g[y].push_back(x);
}
dfs(0);
for(int i = 0; i < n; i++)
printf("%d\n", ans[i]);
return 0;
}
Tutorial
Tutorial is loading...
Solution (Bleddest)
#include<bits/stdc++.h>
using namespace std;
#define sz(a) ((int)(a).size())
struct edge
{
int y;
int c;
int f;
edge() {};
edge(int y, int c, int f) : y(y), c(c), f(f) {};
};
const int N = 100;
vector<edge> e;
vector<int> g[N];
int edge_num[N][N];
int char_vertex[6];
int mask_vertex[N];
int used[N];
int cc = 0;
int s, t;
void add_edge(int x, int y, int c)
{
edge_num[x][y] = sz(e);
g[x].push_back(sz(e));
e.push_back(edge(y, c, 0));
edge_num[y][x] = sz(e);
g[y].push_back(sz(e));
e.push_back(edge(x, 0, 0));
}
int rem(int num)
{
return e[num].c - e[num].f;
}
int dfs(int x, int mx)
{
if(x == t) return mx;
if(used[x] == cc) return 0;
used[x] = cc;
for(auto num : g[x])
{
if(rem(num))
{
int pushed = dfs(e[num].y, min(mx, rem(num)));
if(pushed)
{
e[num].f += pushed;
e[num ^ 1].f -= pushed;
return pushed;
}
}
}
return 0;
}
bool check(int ch, int mask)
{
if((mask & (1 << ch)) == 0)
return false;
int cv = char_vertex[ch];
int mv = mask_vertex[mask];
int e1 = edge_num[s][cv];
int e2 = edge_num[mv][t];
if(e[e1].f == 0 || e[e2].f == 0)
return false;
e[e1].f--;
e[e1 ^ 1].f++;
vector<int> affected_edges;
affected_edges.push_back(e1);
for(auto x : g[cv])
{
if((x & 1) == 0 && e[x].f > 0)
{
affected_edges.push_back(x);
e[x].f--;
e[x ^ 1].f++;
int y = e[x].y;
for(auto x2 : g[y])
{
if((x2 & 1) == 0)
{
affected_edges.push_back(x2);
e[x2].f--;
e[x2 ^ 1].f++;
break;
}
}
break;
}
}
if(e[e2].f < e[e2].c)
{
e[e1].c--;
e[e2].c--;
return true;
}
affected_edges.push_back(e2);
e[e2].f--;
e[e2 ^ 1].f++;
for(auto x : g[mv])
{
if((x & 1) == 1 && e[x].f < 0)
{
affected_edges.push_back(x ^ 1);
e[x].f++;
e[x ^ 1].f--;
int y = e[x].y;
for(auto x2 : g[y])
{
if((x2 & 1) == 1)
{
affected_edges.push_back(x2 ^ 1);
e[x2].f++;
e[x2 ^ 1].f--;
break;
}
}
break;
}
}
cc++;
e[e1].c--;
e[e2].c--;
if(dfs(s, 1))
return true;
else
{
e[e1].c++;
e[e2].c++;
for(auto x : affected_edges)
{
e[x].f++;
e[x ^ 1].f--;
}
return false;
}
}
char buf[100043];
string allowed[100043];
int allowed_mask[100043];
int main()
{
s = 70;
t = 71;
scanf("%s", buf);
string z = buf;
int n = sz(z);
int m;
scanf("%d", &m);
for(int i = 0; i < n; i++)
{
allowed[i] = "abcdef";
allowed_mask[i] = 63;
}
for(int i = 0; i < m; i++)
{
int idx;
scanf("%d", &idx);
--idx;
scanf("%s", buf);
allowed[idx] = buf;
allowed_mask[idx] = 0;
for(auto x : allowed[idx])
{
allowed_mask[idx] |= (1 << (x - 'a'));
}
}
for(int i = 0; i < 6; i++)
char_vertex[i] = i;
for(int i = 0; i < (1 << 6); i++)
mask_vertex[i] = i + 6;
for(int i = 0; i < (1 << 6); i++)
for(int j = 0; j < 6; j++)
if(i & (1 << j))
add_edge(char_vertex[j], mask_vertex[i], 100000);
for(int i = 0; i < 6; i++)
{
int cnt = 0;
for(int j = 0; j < n; j++)
if(z[j] == 'a' + i)
cnt++;
add_edge(s, char_vertex[i], cnt);
}
for(int i = 0; i < (1 << 6); i++)
{
int cnt = 0;
for(int j = 0; j < n; j++)
if(allowed_mask[j] == i)
cnt++;
add_edge(mask_vertex[i], t, cnt);
}
int flow = 0;
while(true)
{
cc++;
int p = dfs(s, 100000);
if(p)
flow += p;
else
break;
}
if(flow != n)
{
puts("Impossible");
return 0;
}
for(int i = 0; i < n; i++)
for(int j = 0; j < 6; j++)
{
if(check(j, allowed_mask[i]))
{
printf("%c", j + 'a');
break;
}
}
puts("");
}










How did you got that diff_i formulae in E?
Suppose there is a rest site right before the kilometer we are trying to cross. The probability of this is 0.5 (and then we get a1 as the difficulty).
Ok, suppose then there is no rest site at position i - 1, but it is at position i - 2. The probability of this is 0.25, and then we get a2 as the difficulty.
Then we consider the option when there is a rest site at position i - 3, but no rest sites at position i - 2 and i - 1. The probability of this is 0.125, the difficulty is a3.
And so on, until we get to position 0.
Roger that ^_^
In the solution code the cur is calculated by multiplying a[i] with power of 2. But in the tutorial it was a[i]multiplied by 1/power of 2. Can you please explain this?
Also I didn't understand the last line of the tutorial where diff[i+1] was derived with the help of diff[i]. Thank you very much.
Is there a reason for bounds on F to be 10^6 instead of something a bit smaller like 2*10^5? The problem ended up being pretty hard to solve in Java even with the intended solution. I understand not wanting more naive solutions to pass though.
Probably to disallow the solution with euler tour and sqrt-decomposition.
why would a linear solution fail? maybe you lost time in reading input just like me.
Java is about 5x slower than C++, so many times, perfectly fine solutions in C++ fail in java. I've had java solutions fail many times because I was using long instead of int, or an arraylist/customdatastructure instead of an array, or recursion instead of iteration. I've also gotten accepted verdicts by rewriting slow java code in c++.
Though you can lose time reading input with scanner, there are many other ways to lose time, ways that C++ or even python uses don't need to care about. I don't think any accepted solutions in java for this problem used recursion, but many did in C++.
Case and point: When I made this comment, there were 25 accepted c++ solutions and 6 TLE c++ solutions. Java had 36 TLE solutions (from 6 distinct people) and only 10 accepted solutions (from 6 distinct people).
As mentioned by Redux on Announcement page, problem D can be solved by using recurrence relation such that if
(a,b)is a co-prime pair then(2a - b, a),(2a + b, a)and(a + 2b, b)are also co-prime wherea > b.Base cases are
(2, 1)for even-odd pairs and(3, 1)for odd-odd pairs. The list is also exhaustive as mentioned in this link so there is no overlapping also. The only breaking condition will bea > nor whenmco-prime pairs are stored.In this way, we will always jump to only co-prime pairs rather than checking every other pair.
So time complexity will also be much less than one given in editorial (Correct me if I am wrong).
Lets say you check that m>=n-1 and phi(2)+...+phi(n)>=m. The probability of gcd being 1 is O(1) so we can randomly generate edges and check if gcd is 1. If we use map complexity will be: O(n+mlogm). But one can also prove that without randomizatiom complexity is O(n+m).
We don't need to check phi sum as one can just store the pairs and if the no. of pairs are less than m, then it is impossible.
Problem G is almost same as the problem Poetic Word from ACM-ICPC Amritapuri Regionals 2017.
Is it, really?
Yes, the main idea of solution is similar, but checking if we can build the suffix when n = 200 and when n = 105 is, I suppose, "a bit" different.
Yeah, the main idea is the same. The difference is in the way to optimize it and using the fact that the alphabet size is small to create less number of nodes by using masks.
My solution 40344721 for problem E. I think it's easier
I also use this method.
But I don't know how to prove that
Sequence from https://oeis.org/A001792.
My proof: (n-segment means segment of length n).
a[i] = 1, 3, 8, 20, 48 ... a[0] = 1, because a n-segment can be paved with a n-segment in one way. a[i] is equal the number of ways to pave the free parts of the n-segment for all possible positions of the segment of length >= n-i. (statement 1)
System: a[0] = 1 a[i] = a[i-1]+2*2^(i-1) + Σ 2^(k-1)*2^(i-k-1) (from k=1 to i-1) = a[i-1]+(i+3)*2^(i-2), for every i>=1.
Clarification: a[i-1] — because we count for all segments of length >=n-i.
2*2^(i-1) is equal the number of ways to pave the free parts in case 1 in pic.
Σ 2^(k-1)*2^(i-k-1) (from k=1 to i-1) is equal the number of ways to pave the free parts in case of movement (n-i)segment, where 2^(k-1) — left part, 2^(i-k-1) — right part. (case 2 in pic)
Proof of "The number of ways to pave the n-segment by k segments is ((n-1)!/(k-1)!)/(n-k)!" you can find here http://kvant.mccme.ru/pdf/1999/05/kv0599levin.pdf after 11-task (it is on russian lang, but i cant find this in english). The number of ways to pave the n-segment by different segment is sum and equals 2^(n-1).
Sorry for my bad english, i used google translate.
Sorry, i forgot to attach the pic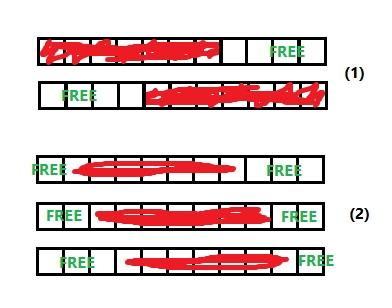
I got a more intuitive prove!
define F(n,k) as number of distance notless than k. So the final result is Σ(k=1~n) F(n,k)*ak.
F(n,n) = 1
F(n,n-1) = 3
F(n,n-2) = 8
F(n,n-3) = 20
...
It's easy to see that F(n,k) = F(n-x,k-x) when k>x.
F(1,1) = F(n,n) = 1
F(2,1) = F(n,n-1) = 3
F(3,1) = F(n,n-2) = 8
F(4,1) = F(n,n-3) = 20
...
So, rewrite the result as Σ(k=1~n) F(k,1) * ak
F(1,1) =1
for F(k,1) , we calculate F(k+1,1): insert a new gap 1' between 0 and 1, it can be a stop , or not stop, and this covers all situations,
if the 1' is a stop, it contribute F(k,1) + 2^k , 2^k from 0 to 1', the others remain F(k,1)
if the 1' is not a stop, it contribute F(k,1) also, because, F(k,1) means count all gap nums, insert a nonstop don't change the gap nums.
Together we get F(k+1,1) = F(k,1)*2 + 2^k.
✿✿ヽ(°▽°)ノ✿
What does " "pull" our depth arrays upwards" means? Thanks in advance..
Assume that u is a child of v and the depth array of u is d[u] = [1, 2, 2]
You want to create the depth array for v (d[v] = {1, 1, 2, 2]), but without creating it from scratch (which would take O(n) time).
Using maps instead of arrays allows to do this in time, and using vectors with the reversed depth arrays allows doing it in even O(1).
time, and using vectors with the reversed depth arrays allows doing it in even O(1).
In the add method of struct state, if (*a)[i] == (*a)[cur_max] then don't we need the min(i, cur_max) as dominant index according to given conditions? Thanks in advance..
Yes, but he did compared also the index with pairs, so this case is already included in the editorial solution.
In the add method we are comparing pairs (val_at_i, i) and (val_at_cur_max, cur_max), if both the values are same then we are updating cur_max if i > cur_max. If the values are same we want to change the value of cur_max only if i < cur_max according to given conditions. Did I miss something?
His depth vector is reversed.
Ohh.. thanks for replying, got my mistake
code In this solution of problem F,he is just forming depth array of all the nodes in the form of array of maps ,and using the factor of logn ,pulling up the maps and merging smaller into bigger at all stages ,but why is he not getting MLE ....as if tree is linear,then space would be O(n^2) UPD:GOT IT.....EVERY TIME WE MERGE PARENT AND ITS CHILD ,WE ARE SWAPPING THEIR MAPS(IF SMALLER) AND THEN MERGE,SO SIZE OF PARENT INCREASES AND ITS CHILD DECREASES....
Problem G , author's solution . We can just rebuild the graph with brute force and run dinic on it .
This could pass all tests if we do not use vector .
I tried your idea, and it worked :) I used vectors though, if you were interested in it, you may have a peek: Submission 40553125.
I suppose that if the alphabet size was 7 then this approach would've been to slow (graph would have about 140 edges) while Authors' solution will fit in the limits.
Thank you for your comment and best regards :)
Wow,you have very nice optimize technique !
This is my solution
Which I got TLE*7 before :)
I have a question about the memory complexity of F: since every node's memory is its max "height", when the tree becomes a chain,it will rise to n(n+1)/2, And I can't run the data on my computer,so I wonder if it will get MLE
If the tree is a chain, I believe you will actually only have 1 (mutable) array. All the nodes will point to that same array. Each time you go up the tree you just copy that array and add 1 to it. This works since you never need to use arrays lower down in the tree again
I am a little confused by the D solution given in the tutorial.In my opinion the
O(N^2*log(N))is not going to fit in time because, as i know the time formula =TimeComplexity(MAXN)/10^9which isO(N^2*log(N))/10^9and converting N to MAXN(10^5) is(10^5)^2*log(10^5)/10^9 seconds,10^10*16/10^9 = 160 seconds. Correct me if i am wrong(i am 100% wrong but i would like an explanation why). As i know from my little experience aO(N^2)solution for a TimeLimit of 2 second a MAXN of 10^5 is way to big.The program in this case terminates much faster because only at n = 600, we already get M >= 100000.
how? can u explain
For problem F, first example, why is the output 3 2 1 0 wrong? There may be several dominant indices for given node, right?
No,dominant index needs to have largest frequency and as closest as possible to the parent node
Yeah, thanks, I misread it.
The problem is asking for the minimum index of the maximum element in the array. Therefore, there is only 1 dominant index.
The array of vertex 1 is: [1, 1, 1, 1, 0, ...] => answer is 0. The array of vertex 2 is: [1, 1, 1, 0, ...] => answer is 0. The array of vertex 3 is: [1, 1, 0, ...] => answer is 0. The array of vertex 4 is: [1, 0, ...] => answer is 0.
For problem 1009 D, how is it sufficient to prove that graph has m valid edges in order to make sure that graph is connected? (Like what I can't get is when is the program making sure that graph that it prints is "connected"?)
It isn't sufficient, you need to do both checks.
The graph which program prints is connected, right? But how can we say that?
In the line, forn(i, n) for (int j = i + 1; j < n; ++j), we are making sure that the graph we built is connected because in the very first loop when i = 0, we are connecting the vertex 1 with all other vertices for j = 1 to n-1, thus making it a connected graph.
okay. Thank you.
1 is coprime of all numbers, hence in the first iteration itself(if m>=n-1) you are making the graph connected.
In this hacked solution, I used
long doublefor the answer, and added up the intermediate means. The editorial says10 bytefloat will pass. So, how many bytes doeslong doubleuses?8? If so, how can we use a10 byteor larger float in C++? I know I could've done this by first calculating sum usinglong long int, but just want to know out of curosity, it may help in some future contests. Thanks :)My submission for E: http://codeforces.com/contest/1009/submission/40471843 Can someone tell me where the overflow is happenning and how to fix it?
There's a subtraction in line 26, and if it could be negative, you have to consider it becomes negative. If your procedure is correct, you may fix it by adding mod in line 26.
In C++11 or above, modulo (by using '%') for negative integer, it will be negative integer from (1-mod) to 0.
(But sadly, I checked your solution with simple fix got TLE. And finally, I cannot remove TLE... My solution is calculating 2^n every time (and this method is slower than yours) but got AC, so I think the cause of TLE is twice multiplication in loop... Sorry for failing to get AC. Someone, please help!)
My AC sol : https://codeforces.com/contest/1009/submission/40479814
My submission for checking (removed WA, but TLE) : https://codeforces.com/contest/1009/submission/40481944
EDIT : I had to say the cause of WA of your original submission is not overflow.
ai is always positive. Since diff[i] is sum of ai divided by positive numbers(2^n), it is also always positive. So I don't understand what could be negative and why we should add mod. Also where are taking mod for a negative integer, the minus sign is outside the multiplication?
On modulo, increasing numbers cannot be always increasing numbers. For example, [10, 20, 30] mod 11 is [10, 9, 8]. Similary, (ai * 2^(n-i)) > (ai * 2^(n- i-1)) is true on integer, but not always true on modulo.
Understood. Then shouldn't we multiply by -1? By adding mod we will get something else right?
You can multiply negative numbers, and also subtract, divide(if mod is prime).
When the number is negative, add mod and you can get right value.
And more, considering the value is big or already positive, you can write like this.
ans = (ans % mod + mod) % mod;
I often write something like this!
Understood what you're saying. Thanks for being patient!!!
(nested deeply, so I wrote here)
I finally got AC by fixing your submission!
https://codeforces.com/contest/1009/submission/40486361
I added this.
ios::sync_with_stdio(false), cin.tie(0);
Just with this, the TLE is removed.
Note that if there are many inputs, you must write it or use only scanf and printf. It is faster!
good luck!
Thanks!
Problem B : I never understood this line.Even till now
String a is lexicographically less than string b (if strings a and b have the same length) if there exists some position i ( 1 ≤ i ≤ | a | , where | s | is the length of the string s ) such that for every j < i holds a [j] = b [j] , and a [i] < b [i] .What is string a ans string b, and indices i and j. What I understood was that string a is the output, and string b is the input string..!!!`` I cant get the relation between editorial explanation with the above statement given in the question. Help me pls regards ;)
String a is lexicographically less than string b if the person with name a is earlier in a phone book than the person with name b.
ok.... thanks for your answer... :)
so it means in their world, there are only alphabets {0,1,2} 0 < 1 < 2 in the order. i got that. But the conditions : i < j and a[j] = b[j].... and a[i] < b[i].
i/p : 100210
o/p : 001120
what is i and j in this case .... ? Regards :)
i is 0
40500124,(AC),40499958,(MLE)
For the problem 1009F's solution, and in the Struct state, why i used "vector a" and got the MLE while i used "vector *a" and got the AC? Thanks in advance...
I would like to share another approach to solve D, though it runs slower and harder to code. (Sorry for the poor English beforehand.)
Let rp[i] be a set storing all j <= n, such that gcd(i, j) = 1.
When constructing rp[i], we can count total number of pair (i, j) such that j > i and j is in rp[i], and terminate when this number >= m.
It is clear that the total number of found numbers won't exceed 2m + n when we stop.
The basic case, rp[1], is all integers in [1, n].
To construct rp[i], first we pick maximum prime factor p (can be found by sieve) of i, "remove" it from i. Formally, let i = p1k1 * p2k2 * ... * pzkz * pk, pi are primes, then we calculate the value temp = p1k1 * p2k2 * ... * pzkz, it can be found in O(logpn) by dividing i by p while i % p == 0.
Since gcd(i, j) = 1 if and only if (i, j) share no common prime factor, we have
rp[i] = rp[temp] - set of all numbers in rp[temp] which has prime factor p.
We can simply iterate through rp[temp] from small to large, when we found a number x, check whether it can be divided by p, and add it to rp[i] if it cannot.
By doing so, we may fail (found a number x but doesn't add it to rp[i]) many times, but for at most O(logpn) failures there must be one success (add x to rp[i]) before all those failures, because when we fail for some x = p1k1 * p2k2 * ... * pzkz * pk, we must have add y = p1k1 * p2k2 * ... * pzkz to rp[i] before. Since x <= n, k can only be numbers picked from [1, floor(logpn)], thus each success corresponds to at most O(logpn) failures.
Because p must be greater than 2, and success always comes before failures, this algorithm runs in O((n + m) * log2n).
Here is my submission
Please correct me if I am wrong.
UPD.
I am stupid, simply let temp = i / p and the arguments still hold.
UPD2.
Also we can store j only for j > i and gcd(i, j) = 1 in rp[i]. The number of operations is smaller than or equal to the previous one.
submission
Question 1009C: Annoying Present
I am getting a relative error = '0.0000206' in test case 9. I am using a double type variable to store the mean values for each new transformation. I have no clue how to reduce the error for the result. My code is here : https://codeforces.com/contest/1009/submission/40511515.
Any help is appreciated.
Every single floating point operation causes precision error. Try to replace them by integer operations as many as possible.
For example, you can sum up all x by integer operations, and add it to mean at last. In this way we use just a single floating point operation rather than O(m) floating point operations, therefore the precision error can be reduced.
The same trick can also be applied to d.
My solution for Prob.E. Maybe it's better??
One Way to prove this:
my solution of F says Stack Overflow can someone suggest me some way to manage it on Test 131
can you help me on test case 105 my solution.
Can anyone give a more intuitive explanation to the solution of problem G? I understand what's being done, but not why it's being done. Such as why are we decreasing the flows in the path and stuff.
Another (probably harder) way to solve E: We need to consider all possible partitions of a sequence of length N. We know that each chunk of length X in each partiton will add prefix_sum(X) to the answer, so we need to calculate number of chunks of length X for all possible Xs in all possible partitions. This is https://oeis.org/A045623 . There are a lot of different formulas to caluclate this (but I don't know how to derive them to be honest).
Can anyone tell me why I got wa in first solution but ac in second solution in problem C?The difference between these two is the variable type.
first solution:https://ideone.com/qEkY5S
second solution:https://ideone.com/vuRdGW
In the solution code the cur is calculated by multiplying a[i] with power of 2. But in the tutorial it was a[i]multiplied by 1/power of 2. Can anyone please explain this?
Also I didn't understand the last line of the tutorial where diff[i+1] was derived with the help of diff[i].
Why O(N2LOGN) is fast enough in D? i need explanation
G can be solve within a better Time complexity O(A^2n)。
It can be viewed here(In Chinese)
Code: