Tutorial
Tutorial is loading...
Solution (Vovuh)
n, k = map(int, input().split())
print((k + n - 1) // n)
Tutorial
Tutorial is loading...
Solution (Vovuh)
q = int(input())
for i in range(q):
n, m, k = map(int, input().split())
if (n < m): n, m = m, n
if (n % 2 != m % 2):
k -= 1
n -= 1
elif (n % 2 != k % 2):
k -= 2
n -= 1
m -= 1
print(-1 if k < n else k)
Tutorial
Tutorial is loading...
Solution with combinatorics (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
long long C[20][20];
long long pw[4];
long long cnk(int n, int k){
if (k < 0 || k > n) return 0;
return C[n][k];
}
long long get(int n, int lft){
long long tot = 0;
forn(i, lft + 1)
tot += cnk(n, i) * pw[i];
return tot;
}
long long calc(long long x){
string s = to_string(x);
long long res = 0;
int cur = 3;
int n = s.size();
forn(i, n){
if (s[i] == '0') continue;
res += get(n - i - 1, cur);
--cur;
if (cur == -1) break;
res += get(n - i - 1, cur) * (s[i] - '1');
}
return res;
}
int main() {
forn(i, 20){
C[i][0] = C[i][i] = 1;
for (int j = 1; j < i; ++j)
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
}
pw[0] = 1, pw[1] = 9, pw[2] = 81, pw[3] = 729;
int T;
scanf("%d", &T);
forn(i, T){
long long L, R;
scanf("%lld%lld", &L, &R);
printf("%lld\n", calc(R + 1) - calc(L));
}
return 0;
}
Solution with precalc (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
vector<long long> res;
void brute(int pos, int cnt, long long cur){
if (pos == 18){
res.push_back(cur);
return;
}
brute(pos + 1, cnt, cur * 10);
if (cnt < 3)
for (int i = 1; i <= 9; ++i)
brute(pos + 1, cnt + 1, cur * 10 + i);
}
int main() {
brute(0, 0, 0);
res.push_back(1000000000000000000);
int T;
scanf("%d", &T);
forn(i, T){
long long L, R;
scanf("%lld%lld", &L, &R);
printf("%d\n", int(upper_bound(res.begin(), res.end(), R) - lower_bound(res.begin(), res.end(), L)));
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = 300 * 1000 + 9;
int n, m;
int a[N], b[N];
int main() {
scanf("%d", &n);
for(int i = 0; i < n; ++i) scanf("%d", a + i);
scanf("%d", &m);
for(int i = 0; i < m; ++i) scanf("%d", b + i);
long long sum = 0;
for(int i = 0; i < n; ++i) sum += a[i];
for(int i = 0; i < m; ++i) sum -= b[i];
if(sum != 0){
puts("-1");
return 0;
}
int posa = 0, posb = 0;
int res = 0;
while(posa < n){
++res;
long long suma = a[posa++], sumb = b[posb++];
while(suma != sumb){
if(suma < sumb) suma += a[posa++];
else sumb += b[posb++];
}
}
printf("%d\n", res);
return 0;
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 1000 + 7;
struct seg{
int x1, y1, x2, y2;
seg(){};
};
struct line{
long long A, B, C;
line(){};
line(seg a){
A = a.y1 - a.y2;
B = a.x2 - a.x1;
C = -A * a.x1 - B * a.y1;
};
};
int n;
seg a[N];
int get(seg a){
int dx = a.x1 - a.x2;
int dy = a.y1 - a.y2;
return __gcd(abs(dx), abs(dy)) + 1;
}
long long det(long long a, long long b, long long c, long long d){
return a * d - b * c;
}
bool in(int x, int l, int r){
if (l > r) swap(l, r);
return (l <= x && x <= r);
}
bool inter(seg a, seg b, int& x, int& y){
line l1(a), l2(b);
long long dx = det(l1.C, l1.B, l2.C, l2.B);
long long dy = det(l1.A, l1.C, l2.A, l2.C);
long long d = det(l1.A, l1.B, l2.A, l2.B);
if (d == 0)
return false;
if (dx % d != 0 || dy % d != 0)
return false;
x = -dx / d;
y = -dy / d;
if (!in(x, a.x1, a.x2) || !in(y, a.y1, a.y2))
return false;
if (!in(x, b.x1, b.x2) || !in(y, b.y1, b.y2))
return false;
return true;
}
int main() {
scanf("%d", &n);
forn(i, n)
scanf("%d%d%d%d", &a[i].x1, &a[i].y1, &a[i].x2, &a[i].y2);
int ans = 0;
int x, y;
forn(i, n){
ans += get(a[i]);
set<pair<int, int>> pts;
forn(j, i)
if (inter(a[i], a[j], x, y))
pts.insert({x, y});
ans -= pts.size();
}
printf("%d\n", ans);
return 0;
}
1036F - Relatively Prime Powers
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int K = 100;
const int N = 100 * 1000 + 13;
const long long INF64 = 3e18;
int mu[K];
void precalc(){
static bool prime[K];
static int lst[K];
memset(prime, false, sizeof(prime));
forn(i, K) lst[i] = i;
for (int i = 2; i < K; ++i){
if (lst[i] == i) mu[i] = 1;
for (int j = 2 * i; j < K; j += i){
lst[j] = min(lst[j], lst[i]);
if (lst[j] == lst[i])
mu[j] = 0;
else
mu[j] = -mu[i];
}
}
}
int mx[K];
long long binpow(long long a, int b){
long long res = 1;
while (b){
if (b & 1){
if (res < INF64 / a) res *= a;
else return INF64;
}
if (b > 1){
if (a < INF64 / a) a *= a;
else return INF64;
}
b >>= 1;
}
return res;
}
long long calc(long long n){
int pw = 63 - __builtin_clzll(n);
for (int i = 3; i <= pw; ++i){
if (mu[i] == 0) continue;
while (binpow(mx[i], i) > n)
--mx[i];
}
long long res = n - 1;
for (int i = 2; i <= pw; ++i)
res -= mu[i] * (mx[i] - 1);
return res;
}
int get_sqrt(long long n){
int l = 1, r = 1000000000;
while (l < r - 1){
int m = (l + r) / 2;
if (m * 1ll * m <= n)
l = m;
else
r = m;
}
return (r * 1ll * r <= n ? r : l);
}
long long ans[N];
int main() {
precalc();
int T;
scanf("%d", &T);
vector<pair<long long, int>> q;
forn(i, T){
long long n;
scanf("%lld", &n);
q.push_back({n, i});
}
sort(q.begin(), q.end(), greater<pair<long long, int>>());
mx[3] = 1000000;
mx[4] = 31622;
mx[5] = 3981;
for (int i = 6; i < K; ++i)
mx[i] = 1000;
forn(z, T){
long long n = q[z].first;
mx[2] = get_sqrt(n);
ans[q[z].second] = calc(n);
}
forn(i, T)
printf("%lld\n", ans[i]);
return 0;
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 1000043;
vector<int> g[N];
vector<int> gt[N];
vector<int> src;
vector<int> snk;
int reach[20];
int used[N];
void dfs(int x)
{
if(used[x]) return;
used[x] = 1;
for(auto y : g[x]) dfs(y);
}
int main()
{
int n, m;
scanf("%d %d", &n, &m);
for(int i = 0; i < m; i++)
{
int x, y;
scanf("%d %d", &x, &y);
--x;
--y;
g[x].push_back(y);
gt[y].push_back(x);
}
for(int i = 0; i < n; i++)
{
if(g[i].empty())
snk.push_back(i);
if(gt[i].empty())
src.push_back(i);
}
int cnt = src.size();
for(int i = 0; i < cnt; i++)
{
memset(used, 0, sizeof used);
dfs(src[i]);
for(int j = 0; j < cnt; j++)
if(used[snk[j]])
reach[i] ^= (1 << j);
}
bool ok = true;
for(int mask = 0; mask < (1 << cnt); mask++)
{
int res = 0;
for(int j = 0; j < cnt; j++)
if(mask & (1 << j))
res |= reach[j];
int cnt1 = __builtin_popcount(mask);
int cnt2 = __builtin_popcount(res);
if(cnt2 < cnt1 || (cnt2 == cnt1 && cnt1 != 0 && cnt1 != cnt))
ok = false;
}
if(!ok)
puts("NO");
else
puts("YES");
}
I found a strange thing in F. Two ACs codes output different result. Detail in https://codeforces.com/blog/entry/61728. Can anyone help me?
Can someone prove the author's solution for B?
i thought about this problem lot after the contest.
what i came up with is that there is 8 cases for m,n,k: odd/odd/odd, odd/odd/even....even/even/even. all cases reduce down to the odd/odd/odd case or the even/even/even case. we can see that it is possible to solve the odd/odd/odd or even/even/even case using all diagonal moves as long as m,n is reachable in k moves.
for an example of "reduction", the even/odd/odd case reduces to the even/even/even case because you can "spend" one non-diagonal move in the n-direction. [1]
the author's solution is basically "reducing" down all cases to o/o/o or e/e/e cases with mod. see my coded sol here: 42690270
[1] in fact, the o/o/o case reduces down to the e/e/e case by spending 1 diagonal move
We can change the problem to this: you should use 1/-1/0 k times totally to get m and n respectively.(remember that m and n are nothing to do with) And according to the problem and greedy algorithm the num of 1/-1 should be as much as possible.
for m we should at least use 1 m times and if k<m then it is impossible to get to (m,n) if k==m then for m we are done if k>m then we can add the combination of (1 and -1), then the left (m-k)%2(1 or none) should be 0. for n we do the same.
so now for m and n, the num of 0 should be at least (m-k)%2 and (n-k)%2 respectively. And for the 0 in m, we must use a 1/-1 in n to construct a valid move (0,1) or (0,-1), the same for n. at last there are (m-k)%2+(n-k)%2 moves not diagonal, so the answer is k-(m-k)%2-(n-k)%2.
Randomized solution for problem G: here
cool.
I will try to explain why this solution works: obviously (unless I missed some bug of course, but from conceptual standpoint the solution seems pretty sound), the solution in question can make only one type of mistake: answer "YES" when the actual answer is "NO".
When the answer is "NO"? When there is at least one "bad" permutation of numbers from 1 to k. I will show that in this cases there are actually a lot more bad permutations than just one. Indeed, consider the set X from the editorial.
To explain the main idea lets consider the simplest case when |X| = |f(X)|. Then any permutation that matches elements of X only with elements of f(X) and matches elements {1, 2, ..., k} - X with elements {1, 2, ..., k} - f(X) is a bad permutation: when doing a graph walk starting with some source in X, we will never leave reach any source not from X. Therefore there is at least |X|!(k - |X|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.
To deal with the case |f(X)| < |X|, we will take some subset Y of X with size |f(X)|, then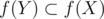
and we can similarly show that all permutations that match sources from Y to sinks in f(X) and sources not from Y to sinks not from f(X) are bad permutations. Therefore there is at least |Y|!(k - |Y|)! ≥ [k / 2]![(k + 1) / 2]! bad permutations.
All in all, if there is one bad permutation, there are at least [k / 2]![(k + 1) / 2]! of them. So the probability of finding a bad permutation randomly is at least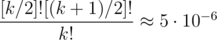
in the worst case of k = 20. From the other hand, on my computer, the code in question checks 
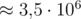random permutations before timing out. In the end, the probability of failure is something of the order ≈ 10 - 8, which is good enough.
cool
Wasted 1 hour trying to solve a harder version of Problem C. I thought classy numbers were those number which had the number of distinct non zero digits <= 3. And when TC 2 and 3 were not passing, I tried so hard debugging.
After successfully wasting 1 hour, read the question again and BAM!!
what it mean prefix in the tutorial for C??
The data for G maybe too weak? I can easily hack my code.
The problem A is so easy, but I solved it late because of my poor English and my poor wi-fi.
In problem E, Can anyone please give proof of why exactly GCD + 1 value will give integer co-ordinates?
Spoiler
Thanks ^_^
[Deleted]
http://codeforces.com/contest/1036/submission/42706346 can someone pls point out the mistake i am making. upd :: got it
In Problem G, it is possible to find for every sources all achievable sinks in a linear time. For this it is necessary to store in each visited vertex an integer (the set of bits of achievable sinks).
Can you explain the approach behind recursion in problem C?
Can problem F be solved with some precalculations (generations of correct numbers), simular to problem C?
can anyone explain classy numbers editorial ??
there is a easy way to solve problem C with DP :) 42742195
It seems to be an interesting approach, but I don't really understand it. Could you please explain it briefly?
f(i,j)means The i th bit of a number(unit's digit,ten's digit...) and already has j non-zero digits.DP uses
flagto control upper bound.If it is not the upper bound,we can remember the result off(x,y).(That's why I initializefto -1 and updatef(x,y)when flag=0).f(x,y)will be accessed multiple times, so we can speed it up by remember it .My English is poor( I use the google translate QAQ ).
Thanks.I can't understand about how (!flag&&~f[x][y]) works,what's mean ?it's mean if f[x][y] has been calculated ,then return f[x][y]? to be honest i want to use pinyin.
Why dont we use -C instead of C? I read in internet that the formula will use -C instead of C? I mean this fragment: long long dx = det(l1.C, l1.B, l2.C, l2.B); long long dy = det(l1.A, l1.C, l2.A, l2.C);
By the properties of determinant
det(-a, b, -c, d) = det(a, -b, c, -d) = -det(a, b, c, d)Ahh it is used then when he does: x = -dx / d; y = -dy / d; right?
Why is Problem A tagged with FFT ? Is there a solution with FFT as well ?
Nope, it means an idiot is going around and trolling.
very very good~ !!
E has a tag "fft". Can it be done using FFT too? If yes, then how?
Honestly, do you even know how to use FFT in the first place?
I do. I'm looking for more questions to practice it.
For problem 1036E — Covered Points , can anybody explain what's special with the test 14? I've seen some people failing this test.
Could someone explain how mobius function could be used in problem F. All I understood is that we are trying to remove the bad elements from the answer. Basically, could someone explain me the formula?
in problem G, how about a 4-vertex graph: 1->2, 3->2, 3->4 ??? It's obvious that 1 is a source but the set of sink it can reach is just {2}???
is there a proof for problem b ?
Can someone explain the brute force generation for C
pos represents the number of digits,cnt represents count of non-zero digits and cur represents the value generated. first we take the generated number and multiply by 10 and increasing number of digits. if a number is classy number then its multiple of 10 will also be a classy number. then we check if the number has less than 3 non-zero digits or not.if it has less than 3 non-zero digits then we can put any number between 1 to 9 at units place and generate another classy number(multiply by 10 and adding the number). we also increase the count of non-zero digit.
I was really confused. thanks for the explanation.
please can anyone explain the formula in problem C, i dont know why it return exactly the beautiful numbers on [1,X), why cur-- like that, that means for(int cur = 3; cur>=0; cur --) , i think i'll insert s[i] in a set so that its size is cur ... A lot of things i cant understand. I've read PikMike's code and the formula for hours. Help me please.
Proof why GCD works in E
The solution to G reminds me of Hall's marriage theorem, and I finally figured out how to solve it in polynomial time.
Take the graph of sources and reachable sinks. If no perfect matching exists, by Hall's marriage theorem, there is a nonempty proper subset of sources $$$X$$$ such that $$$|X|>|f(X)|$$$, so the answer is NO. Otherwise, we need to ensure that $$$|X|<|f(X)|$$$. This means $$$f(X)$$$ has sinks besides the ones matched to sources in $$$X$$$. Connect each sink to the source it is matched to in the perfect matching. The answer is YES if and only if the the resulting graph is strongly connected.
Code: 67053099
Can anyone explain F with little more details ?
Can someone prove the solution of problem B ?
Could anyone please explain how the dp solution works for C. Here is nicely written version of it, https://codeforces.com/contest/1036/submission/66720126, but I cant understand how it works.