in problem 27E you are asked to find the smallest positive integer which has exactly n divisors .
how to solve it > >
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
in problem 27E you are asked to find the smallest positive integer which has exactly n divisors .
how to solve it > >
| Name |
|---|



We denote the number of divisors of a number x, as d(x). It can be proven that d(x) = (e1 + 1)·(e2 + 1)·...·(ek + 1) , where x = p1e1·p2e2·...·pkek is the prime factorization of x.
We notice that it's optimal for p1 to be as small as it can be, so it should be equal to 2. We notice the same for p2, so it should be equal to 3. It is optimal to take the smallest possible prime every time. So we should only take the first k primes. But consider the case where ei = 1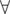 i. We see that if we take more than pk = 41 (approximately), we are way over our limit of 1018 for our answer. So our list of primes should be up to 41.
i. We see that if we take more than pk = 41 (approximately), we are way over our limit of 1018 for our answer. So our list of primes should be up to 41.
Now we try to construct the desired number by some kind of trial-and-error. As long as we can multiply our current number with the current prime raised to some power ei, we test for this situation, going to the next prime, knowing the current number's divisors and its value. Notice that every prime should not fit more than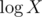 times in some number X, and we only have about 15 primes, so operations aren't too much.
times in some number X, and we only have about 15 primes, so operations aren't too much.
Solution link: 43224863
thanks.. charis .. i got it...
trying every possibility in brute force way to get the minimum number...
ur solution is very clear... :))
You can bring down the operations even more, considering the fact that e(i)>=e(i+1) in the optimal solution.
Yes, you are right. Holding an extra parameter for ei - 1 and starting ei from there instead of 1. I believe you can also use dp on this idea if you modify it a little, but I don't think it's necessary.
Fun fact: You missed 23 in your list of primes Luckily it didn't affect the solutions in this case :p