Let's discuss the problems.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/27/2024 03:39:52 (h1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How to solve A, E, H?
E: I used Java Biginteger since the numbers were too big.
We can represent the points on the first segment as parameter of t. If A and B are vector to the two end points, then an arbitrary point on AB is: tA + (1-t)B = t(A-B) — B. Similarly we can express a point on the second segment as parameter of s: s(C-D)-D.
Let's compute distance-squared between these points: sum[t(A-B) + s(C-D) + D — B]^2 [sum is over each of the coordinates] = sum[tE + sF + G]^2 (*).
To minimize this sum, we can partially differentiate with respect to t and s and hence we will get two equations: t(sum-of-E^2) + s(sum-of-EF) + (sum-of-GE) = 0 and t(sum-of-EF) + s(sum-of-F^2) + (sum-of-GF) = 0. Solving them we will get s and t.
And then we can plug value of s and t to (*) we will get the answer.
There is a corner case where the lines are parallel with the same direction vector. In such situation, we will have only one equation instead of 2. I plugged in s=0 to get a value for t, and the remaining part was same.
A: Find SALT with precalc. First find all numbers that satisfying second array (~4000 numbers). Then from that 4000 numbers find that number which satisfying first array.
How would you do this precalc? My simulation was too slow.
Notice that you can go from the end (previous seed is determined uniquely)
Modulo was 2^31, so division is not unique right?
You multiply by odd number, so it is. All coprime numbers have unique inverse.
So, is it like: [reference: 1 3 2 3 0 0 4 2] 1. loop over 0..2^31-1 and see if it's %5 = 2, 2. if so, find the previous seed, and check %5 = 4 ...
if all 8 passes, then this is a candidate.
So running over 2^31 numbers and doing something like 8 operations.
Is this your simulation? And it runs in reasonable time?
Yes, but you continue after that to previous numbers (10k times go back for each number), It leaves only 1/5 of numbers each time so it works faster then is mod*8, it's like mod*5/4 or so, it's not so much especially considering you almost don't use memory
I used two steps:
Even better: we can bruteforce only "good seeds after 80k iterations skipped", and then only with the succeeding seeds perform 80k roll-backs and checking that power sequence is the same as we want.
A way to do it without reversing the random number generator is to use a circular buffer for the random values.
Start with some seed. Compute the first 80 008 pseudorandom values and put them in an array. Look if the last 8 values, pseudorandom numbers with indices 80 000-80 007 in the array, give the required
Genearray if takenmod 5. It happens fairly rarely, like 231 / 58 times. If it did happen, use the previous 80 000 values to slowly check thePowerarray.Now suppose it didn't work on the first try. Generate the next random value, and check for the numbers with indices 80 001-80 008, all
mod 5, that they give the requiredGenearray. Then generate the next random value and check the numbers with indices 80 002-80 009, and so on.Lastly, note that we should store only the last 80 008 pseudorandom numbers in this approach, so use a circular buffer to store them: for example, an array of size 131 072 which is accessed as
Index mod 131072every time we use it.This approach takes 3-4 minutes to check all 231 possible values of
Salt(and probably finds the right one a bit faster, depending on where you started).The
Genearray is not necessary at first glance, but actually makes our task easier as shown above. But there is also a fast approach which does not use it. Same as above, start with some seed and generate 80 000 first pseudorandom numbers ri. Calculate the sum of r0 to r9999, the sum of r10 000 to r19 999, and so on until the sum of r70 000 to r79 999. If they are the eight sums we need, great! Otherwise, it's easy to obtain the next eight sums r1 to r10 000, ..., r70 001 to r80 000 from them: for each sum, just subtract the first element and add the next one. And so on: generate the next pseudorandom value, get the next sums in O(1) each, check the eight sums, proceed if they don't match.H: Since the maximum area could be 10^30, I coded it in Java (BigInteger) [not sure if there is __int128 in yandex, never used it before]. Barely made it pass in 1.8s after several TLEs. Any better solution?
My solution was: binary search on the coordinates one by one. Since coordinate value can be 1000, so at most 10*log(1000) ~ 100 call to a function which says true/false to the question, whether the area of the big box is same as union of other boxes (after cutting those boxes by the query box). The union of other boxes can be computed by Inclusion-Exclusion.
We used random modulo in C++ to compare volumes. Still had to optimize a bit
There is no need in binary searching over all values for a coordinate. The answer always coincides with some of the b_i, it gives log 10 instead of log 1000 and works fast enough. I used __int128 and didn't have to do any extra optimizations.
After coordinate compression, the area is only 4010 so no need for BigInteger.
__in128_t, c++, yandex. AC :)
How to solve I?
Give N distinct random odd numbers, so all of them has inverse.
Then take a number from the given N / 2 number, and multiply this with inverses of your numbers. So you have N candidates for X.
Now try other numbers from those N / 2 numbers and in each step you'll get another N candidates for X, but only keep the intersection of these candidates and previous candidates. Since the N / 2 numbers is random, the number of candidates will soon become 1.
How to solve E? I tried to write a solution using __int128, but it seems to be overflowing (not sure, got WA on test 12 and TLE in Pypy on same test). What are the bounds for the final result?
The limit is about 1045-1046 for numerator and 1030-1031 for denominator. We used BigInteger in Java.
How to solve C?
Let's consider some pair of vertices (u, v). Optimal path could be written as a sequence of vertices u = a0, a1, ..., ap = v. Obviously the edge a0 → a1 belongs to some clique A and edge a1 → ap belongs to some clique B. The crucial observation is that if we fix the cliques A and B we are able to find the path between u and v without looking at the individual vertices but only at the cliques. Every edge in the path between u and v belongs to one or several cliques. Let's call a pair of cliques C1 and C2 connected if there exists vertex x belongs to both C1 and C2. The path between u and v could be decribed as a sequence of cliques A = A1, A2, ..., Ap - 1 = B where Ai connected with Ai + 1. It's obvious that with given vertices of the path we can easily find the indices of the cliques. On the other hand given the indices of the cliques we can by definition choose a common vertex for every consecutive pair of cliques and add the starting and the ending vertices.
Let's consider a graph G where each vertex corresponds to a clique and there is a directed edge i → j with the weight aj (weight of clique number j) if i and j are connected. Then for every pair (u, v) such that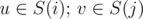 (S(k) is the set of vertices of clique k). dist(u, v) ≤ distG(i, j) + ai where distG is the distance between the cliques i and j in G. distG could be found in O(k3) with Floyd-Warshall algorithm. G itself could be constructed by definition in O(n·k2).
(S(k) is the set of vertices of clique k). dist(u, v) ≤ distG(i, j) + ai where distG is the distance between the cliques i and j in G. distG could be found in O(k3) with Floyd-Warshall algorithm. G itself could be constructed by definition in O(n·k2).
Then all what we have to do is for every pair of cliques (i, j) find the number of vertices such that the optimal path for these pairs corresponds to the path between i and j in G. Let's process pairs of cliques in the increasing order of ai + distG(i, j) and at each step find the number of pairs (u, v) such that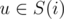 ;
; 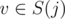 and (u, v) was not considered at previous steps. Then if this number is denoted a x we should increase the answer by x·(ai + distG(i, j)) because for these pairs there is no better path. Let's enumerate
and (u, v) was not considered at previous steps. Then if this number is denoted a x we should increase the answer by x·(ai + distG(i, j)) because for these pairs there is no better path. Let's enumerate 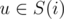 . For every clique i we will maintain set of cliques D(i) such that
. For every clique i we will maintain set of cliques D(i) such that 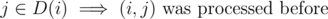 . Denote cliques where u belongs as i1, i2, ..., ip. Pair (u, v) should be counted at this step iff
. Denote cliques where u belongs as i1, i2, ..., ip. Pair (u, v) should be counted at this step iff 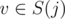 and
and  . Assuming that for every possible set of cliques {c1, ..., cp} we calculated α({c1, ..., cp}) the number of vertices w such that
. Assuming that for every possible set of cliques {c1, ..., cp} we calculated α({c1, ..., cp}) the number of vertices w such that 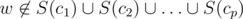 the intended number of vertices u could be found as
the intended number of vertices u could be found as 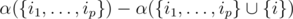 .
.
So, only thing we should do is to calculate α for each of 2k sets of cliques. First of all we can find β(I) the number of vertices belongs to cliques from set I and doesn't belong to any other cliques. Then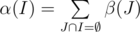 . Even if we calculate alpha in straightforward way enumerating all the subsets of
. Even if we calculate alpha in straightforward way enumerating all the subsets of  one can proof that we will have time complexity O(3k) and it was enough to get accepted.
one can proof that we will have time complexity O(3k) and it was enough to get accepted.
But there is a way to calculate α in O(2k·k). It's easier to calculate α'(I), the number of vertices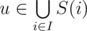 . Let's use dynamic programming: dp[mask][j] (where mask is the string of k zeroes and ones) is the number of vertices w such that for i < j
. Let's use dynamic programming: dp[mask][j] (where mask is the string of k zeroes and ones) is the number of vertices w such that for i < j 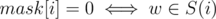 and for i ≥ j
and for i ≥ j  . dp[mask][k] = β(mask). For j < k dp[mask][j] = dp[mask][j + 1] + x where x = 0 if mask[j] = 0 and x = dp[mask'][j] (where
. dp[mask][k] = β(mask). For j < k dp[mask][j] = dp[mask][j + 1] + x where x = 0 if mask[j] = 0 and x = dp[mask'][j] (where 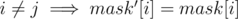 and mask'[j] = 0) otherwise.
and mask'[j] = 0) otherwise.
For every vertex denote M(v) as a string of zeroes and ones such that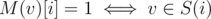 . Then first summand in dp corresponds to vertices with M(v)[j] = mask[j] and the second summand corresponds to vertices with M(v)[j] ≠ mask[j] (if mask[j] = 0 we should not calculate it). Finally it's pretty clear that α'(S) = dp[S][k].
. Then first summand in dp corresponds to vertices with M(v)[j] = mask[j] and the second summand corresponds to vertices with M(v)[j] ≠ mask[j] (if mask[j] = 0 we should not calculate it). Finally it's pretty clear that α'(S) = dp[S][k].
This is it, now we have a solution with time complexity O(2kk2 + n).
How to solve J?
How to solve B and L?
B, very briefly. Let's delete all vertices such that one of the sinks is unreachable from them.
Notice that for every vertex x of a correct machine the set of edges on any path from the source to x contains the same set of edges. It follows from the fact that any path from the source to the 1-sink have to contain all the edges (can you see why?).
Moreover, for every vertex x of a correct machine and for every pair of paths from the source to x and for every vertex of G the parity of the sum of the values of the edges is the same on both paths. The argument is similar to (1).
One can verify (1) and (2) using hashing.
if (1) and (2) hold then f(x) = 1 implies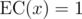 .
.
The only possibility for an error is x such that f(x) = 0 but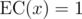 .
.
The case (5) happens if and only if there is a vertex of the machine x labeled with an edge e such that e is not a bridge in the graph G - e'0 - e'1 - ... - e'k where e'1, ..., e'k are the edges on a path from the source to x.
(6) could be verified using disjoint set union with rollbacks.
Solution sketches for some problems:
B:
While traversing through the machine we can watch for a state of the graph -- mask of size k there 1 is corresponding to not satisfied nodes. Initially this mask is equal to the array c. After going along an edge from v to u in the machine state may change -- if this edge was labeled with 1 then values of endpoints of the edge in the graph must be flipped. Our goal is to check if each path to t1 corresponds to an empty mask and if each path to t0 corresponds to a nonempty mask.
in the graph must be flipped. Our goal is to check if each path to t1 corresponds to an empty mask and if each path to t0 corresponds to a nonempty mask.
Let's note some facts about the case then answer is YES:
It is easy to check 1. and find corresponding counterexample if it exists. 2. and 3. can be checked with hashing the state of the graph: generate random zv for each 1 ≤ v ≤ k, hash of the state will be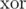 of all not satisfied nodes. It is easy to update this hash then values of 2 nodes in mask changes -- just
of all not satisfied nodes. It is easy to update this hash then values of 2 nodes in mask changes -- just 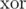 it with
it with  .
.
Now we can assume that if some configuration of edges in the graph leads to t1 then it is really 1. The last thing to check is existence of configuration of edges leads to t0 but have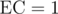 . Consider edge in the machine from v to u such that it is possible to get to t1 from v, but not possible from u. Each path to v uses the same set of edges in the graph and corresponds to the same state of the vertices of the graph. From u we could only get to t0, so the task here is to check whether we can assign some values to not used edges of the graph so that final state will be empty (all k zeros). We can do that iff in each connected component of not used edges xor sum of values of nodes in mask is zero. We can check that using dsu (disjoint set union) data structure with rollbacks: run dfs over back edges of the machine starting with t1. Because in each path to t1 all m edges were used then dfs reaches the node v it will contain exactly connected components of not used edges. To check if state is still ok after going along the edge from v to u it is enough to check if endpoints of
. Consider edge in the machine from v to u such that it is possible to get to t1 from v, but not possible from u. Each path to v uses the same set of edges in the graph and corresponds to the same state of the vertices of the graph. From u we could only get to t0, so the task here is to check whether we can assign some values to not used edges of the graph so that final state will be empty (all k zeros). We can do that iff in each connected component of not used edges xor sum of values of nodes in mask is zero. We can check that using dsu (disjoint set union) data structure with rollbacks: run dfs over back edges of the machine starting with t1. Because in each path to t1 all m edges were used then dfs reaches the node v it will contain exactly connected components of not used edges. To check if state is still ok after going along the edge from v to u it is enough to check if endpoints of  are in the same connected component (in case of edge from v to u labeled with 1 of course).
are in the same connected component (in case of edge from v to u labeled with 1 of course).
F:
If n = k then answer is YES.
Note the following facts:
If the answer if not prefix and not suffix than it is k consecutive maximums of the array. If the answer is suffix of length k than it is nondecreasing and an - k + 1 must be not less than all ai with 1 ≤ i < n - k + 1. The same for prefix. All these cases are easy to check in O(n).
J:
Ask "?" Q times. Select 2 strings from the input, denote them by s' and t'. Let's think that they were generated from different base strings s and t. Cluster all the remaining string in 2 clusters based on distance to s' and t'. Construct S and T by selecting the most frequent digit in each position in corresponding cluster. Check if S and T could generate given Q input strings (each input string has distance exactly K to S or to T). If everything is OK, output S and T.
Let's provide some intuition about correctness of this solution.
What is the probability that some incorrect S and T pass the final check? It means that some 25 strings were generated from s, but some S ≠ s has distance K to each of them. But we can reconstruct s from these 25 strings: with probability ≈ 0.999983 some position was flipped <13 times, and with probability ≈ 0.998312 each position was flipped <13 times. This is a lower bound for the correct probability. In reality situation is even better since we construct S and T in a special way.
So we will win if for some pair of strings s' and t' from the input S and T appears to be equal to s and t respectively. If distance between s and t are big then each string almost certainly will be in correct cluster, if distance between s and t are small then actually small number of positions are unknown and correct configuration of these positions will be found fast.
To solve this problem one don't have to write down some probabilities, because it is very easy to verify correctness of solution locally.
Authors tried to find at least one test run there model solution fails, but didn't succeed.
K:
4 variables fully define the entire table:
* number in the left upper corner;
* difference of adjacent elements in the first row;
* difference of adjacent elements in the second row;
* difference of adjacent elements in the first column;
So one can solve system of linear equations over these variables. Be careful with small tables and thin table.
L:
We have to consider two separate cases: 1) there are two tangent planes, 2) there is only one tangent plane or no tangent planes.
The second case is easier, so we are going to describe only the first case. First of all, we need to understand the structure of the surface of the convex hull. It comprises the following parts: two equal triangles, which lie on two tangent planes; for each pair of spheres there is a part of the cone, tangent to these two spheres; for each sphere there is a part of the surface of this sphere.
It's convenient to start the solution by finding the normals to the tangent planes. If we can't find two distinct normals, then it's the second case and we do not discuss it here. Let O1, O2, O3 be the centers of the spheres. Now, for convenience, we will suppose, that the plane that contains these three points is horizontal, and that the cross product (O2 - O1) × (O3 - O1) is in upwards direction.
Let A1, A2, A3 be the touching points of the upper tangent plane and spheres and let B1, B2, B3 be the touching points of the lower tangent plane. First, we calculate the volume of the polyhedron with the vertices O1, O2, O3, A1, A2, A3. The volume of the polyhedron with the vertices O1, O2, O3, B1, B2, B3 is the same. Next, we should calculate the volume of the parts of the cones. Consider, for instance, the cone between first and second spheres. Consider the three-dimensional shape with vertices O1, A1, A2, O2, B2, B1, with surface that consists of the part of the cone between first and second spheres, rectangles O1, O2, A2, A1 and O1, O2, B2, B1 and also two parts of cones with vertices O1 and O2. It's possible to write down the formula for the volume of such shape. We add to the answer this volume and analogous volumes of shapes between two other pairs of spheres.
Finally, it remains to calculate the volume of the parts of the balls. It's just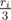 times the area of the part of the sphere. How does the part of the sphere looks like? It's bounded by two arcs of two circles, which are not geodesics. This problem is analogous to the following well-known problem: find the area of the union of two circles on plane. But in our case we should find the area of the union of two circles on sphere. This can be solved in a standard way.
times the area of the part of the sphere. How does the part of the sphere looks like? It's bounded by two arcs of two circles, which are not geodesics. This problem is analogous to the following well-known problem: find the area of the union of two circles on plane. But in our case we should find the area of the union of two circles on sphere. This can be solved in a standard way.
For instance, consider the part of the first sphere. It's a union of two circles on the first sphere. These circles intersect in points A1, B1. Consider the geodesic between this two points. It separates our part of the first sphere in two parts. We calculate their areas separately. Each part is bounded by one geodesic between A1 and B1 and one arc of some circle between these two points. So, we need to calculate the volume of the segment of the circle on the sphere. To do this, we need to calculate the area of the sector of the circle and subtract the area of triangle.
In L, A few questions:
You can check my solution here.
If you would like to look at the solution I used for stress-testing, here it is. This solution does the following: first, we consider a big cube, that contains our spheres. On each step we divide this cube into 8 parts, and remove those parts which lie outside or inside the convex hull. It's hard to check that the cube lies outside the convex hull, so instead of it I check that circumscribed sphere of the cube does not intersect the convex hull. After several steps we are left with some cubes which lie along the boundary. Finally, we can use Monte-Karlo method to calculate the volume of the intersection of these remaining cubes and the convex hull.
Seems that tests for J were weak. Seems that hardest tests against solutions I have seen were s=t=0 and s = neg(t).
You are right, many unexpected solutions passed. We had several solutions which calculated some statistics independently for positions and all of them failed in several tests, but some contestants used slightly different approaches/magic constants and got AC :(
You should just make more tests. Seems that 50 tests of both these types were enough
Yes, more tests is better. Also for some solutions tests with strings different in one position were special, for example.
Usually they also fail on all different. Basically you have problem with two equal letters which looks like different or with two different looks like the same.
Can someone give statements of the problems please?
You can download statements at upper-right corner, near "Jury messages" button.
Is it possible to add the Grand Prix contests to Codeforces Gym? I think there are many people here who want to solve problems of GPs, but are unable to solve due to Sector issue and many more.
How to solve D?
Consider rotating the plane a bit:
The fat squares comprise a grid corresponding to the crosses. There are at least two ways from here:
For each square, find the center square of its cross, and then calculate the Manhattan distance between crosses.
Note that the centers of the smaller squares are in the corresponding cross if and only if they are in the corresponding fat square. So instead of finding the center of the cross, we can just do some rounding.
It's probably will get down to the same formulas, but your interpretation seems beautiful but too hard to actually come up with.
What we did: Suppose we are going from cross center to cross center: Then we will make several(possibly negative number) (2, 1) moves and several (-1, 2) moves. Then just solve linear system of 2 variables and 2 equations. Now, to get cross center we just need to check initial cell and 4 its neighbours to check if they are in the form mentioned in the statement (again, 2x2 linear system. need to check whether answer is integral)
Yeah, my solution, in code, is actually translating coordinates (x, y) into ((2x + y) / 5, (x - 2y) / 5), which is the same thing you will get after solving the system of linear equations.
And I think one way to achieve it is not actually harder than the other. Just that some people prefer visualization, and some other prefer formulas. From the people I've met, both "groups" (in my subjective classification) had individuals which had been very successful at mathematics and algorithms.
We solved exactly as Gassa told. I don't think it was hard.
A: Shouldn't all pet powers be 500? Regardless of seed, Random() multiplies it by 1234567893 (multiple of 3) and adds 151515151 (equal 1 mod 3). Hence, Random() return value will always be 1 mod 3, and inside GenerateRandomPower(), Result value in each iteration will be the same (500). Am I missing anything?
Note that all calculations are made modulo 231. Before we take the value
mod 3, it is takenmod 2^{31}. So the end result may be different after every call.What a silly mistake! Thank you for pointing out!