What are some efficient ways to divide 'a' by 'b' where the range is :
-10^300 <= a,b <= +10^300
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
What are some efficient ways to divide 'a' by 'b' where the range is :
-10^300 <= a,b <= +10^300
| Name |
|---|



Since the answer of
a/bis between 0 and a, we could use binary_search. Complexity:log(a), which is around 1000.That's actually since in every iteration of binary search you need to multiply two numbers.
since in every iteration of binary search you need to multiply two numbers.
Fortunately there's an easier and faster way in O(n2) (hereafter n is the number of digits), assuming the numeric base d is a small constant (typically 2, 10, or 16).
Start with x = 0, then, for each i from n down to 0, keep incrementing x by di as long as xb ≤ a. This "increment and compare" operation can be done in O(n) by performing it not on x, but on the product xb — you can add bdi to any number by simply appending i zeroes to the d-ary representation of b and performing addition as usual. Running time of this algorithm is O(d·n2). For large values of d you can use binary search inside each iteration of the outer loop, instead of a simple loop which keeps adding di, so the complexity becomes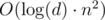 .
.
There is a way to do it in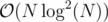 , where N is the sum of lengths of the numbers. Link. But it's masochistic to implement it (as far as I remember).
, where N is the sum of lengths of the numbers. Link. But it's masochistic to implement it (as far as I remember).