Hi everyone! This one will be long and contain a lot of off-topic, prepare yourself (or skip down to solution of mentioned problem)!
Intro
In this blog post I would like to talk about some problem that somehow was on my mind for several years and yet only now I have some more or less complete understanding of how to deal with it. The problem is as follows:
You're given string S and q queries. In each query you have to count amount of distinct substrings of S[l, r].
Since then and for a long time this one was probably the hardest string problem I could ever imagine. In particular I saw some partial cases of it on several judges, which supported my assumption that problem is particularly tough. Some notable examples:
- To Queue or not to Queue on codechef by Gerald. It is the same problem, but queries are formed as queue, i.e. you have to add letter to the right, delete letters from the left and write number of distinct substrings on each turn. This one is from year 2013. This particular problem can be solved in O(n) with some modification of Ukkonen's algorithm to make it work on a queue.
- Chef and Substrings also on codechef by Gerald. This one asks for number of distinct substrings which start on position between l and r. Actual editorial for this one is presumably lost, so I'll appreciate if anyone can share which ideas were used in it. This one is also from year 2013. Meanwhile its constraints make me feel that intended solution had to run in
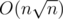 , though it's possible to solve it in
, though it's possible to solve it in  which I will elaborate later on.
which I will elaborate later on. - A problem on Petrozavodsk Summer Programming Camp 2017 asking about number of distinct subpalindromes of substring which also has somehow interesting story behind. I came up with
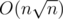 idea using eertree and some kind of Mo's Algorithm back in 2015 and shared it with droptable who invented
idea using eertree and some kind of Mo's Algorithm back in 2015 and shared it with droptable who invented  solution based purely on some scientific palindromic properties. I tried to propose this problem to csacademy then and waited for some feedback in good faith for roughly a year. I didn't receive one but later on Barcelona Programming Bootcamp I was approached by wefgef who said that he remembers that I sent a problem and gave me cool csacademy t-shirt which I oftenly wear now. Well, since then another half a year passed and after all problem was given in Petrozavodsk by droptable.
solution based purely on some scientific palindromic properties. I tried to propose this problem to csacademy then and waited for some feedback in good faith for roughly a year. I didn't receive one but later on Barcelona Programming Bootcamp I was approached by wefgef who said that he remembers that I sent a problem and gave me cool csacademy t-shirt which I oftenly wear now. Well, since then another half a year passed and after all problem was given in Petrozavodsk by droptable. - I also prepared partial case of this problem for Petrozavodsk Summer Camp 2015, MIPT contest. You can find it on timus: 1799. This one asks you to count distinct substrings on all edges of suffix tree and can be solved by compacted suffix automaton in O(n).
And finally there was a problem How many substrings? on hackerrank by SkyDec in 2016. It was unnoticed by me till year 2017 though when izban shared it with me and told that solution is some heavy link-cut tree stuff and that niyaznigmatul knows some better solution which I still don't know. I didn't really studied that solution and I wasn't satisfied since it was  and it used that link-cut tree stuff which I don't know. Up to that time I was coming back to that problem several times but couldn't come up with anything better than
and it used that link-cut tree stuff which I don't know. Up to that time I was coming back to that problem several times but couldn't come up with anything better than 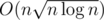 so it still was better than anything I could imagine. So I just marked that the problem has some fast solution and didn't think about it afterwards.
so it still was better than anything I could imagine. So I just marked that the problem has some fast solution and didn't think about it afterwards.
After that came problem Sum of Squares of the Occurence Counts from XVIII Open Cup, Grand Prix of Korea. In this problem you have to sum up squares of number of occurences of all distinct substrings for all prefixes. I came up with heavy-light decomposition on suffix automaton solution, which I wrote down in corresponding comment. Later discussing this problem 300iq shared with me HLD-based solution for distinct substrings on segment, which was too hard for me to understand then.
And most recently I discussed that problem again with izban and 300iq, who suggested to me the problem which was stated as follows:
You're given strings s1, s2, s3 and q queries: how many distinct substrings you can obtain if you cancatenate some arbitrary substrings of s1[l1, r1], s2[l2, r2] and s3[l3, r3].
Which is from some unnamed asian contest if I understood it correctly. We discussed distinct substrings problem once again and during discussion came up with following approach which doesn't use any HLD and works... Well, still in  .
.
Solution
Let's recall one of offline solutions for distinct elements on segment queries. You can group queries by their right end and then, at step r we will keep bi = 1 if i is the last occurrence of ai before r and 0 otherwise. Then you can count distinct numbers by summing up bi for i from l to r. Let's utilize this technique for our problem. To begin with we'll build suffix automaton for whole string beforehand. Remember that suffix link tree of suffix automaton is suffix tree of reversed string!
Now we will drop our string and add letters one by one to the end of string s, but using automaton and its suffix link tree for whole string. We will keep bi to be equal amount of substrings s[i, j] such that j ≤ r and i is the last position when s[i, j] occurs in s[1, r]. Thus to answer queries you'll have to simply sum up numbers from l to r. But how to maintain bi?
For which strings positions will be updated when you add new letter c to the end of s? Well, for all new suffixes, of course, so we'll add 1 to the whole string. Now we should find positions in which those of such strings occurred last time before that. You may note that in suffix link tree you will update position for all substrings on the path from current prefix of s to the root. So to find which substrings you will move you may say that you color path from v to root in color i and if you bump into vertex u colored in j, then it was colored when you were considering prefix s[1, j]. Thus you find next vertex w when the color will be changed (let its color be k) and you subtract 1 on segment [j - lenu, j - lenw). After this you'll repeat the same operation with j → k. In the end you'll fix some amount of segments on the path to the root colored in the wrong color. Each time you'll have to subtract 1 on corresponding segment and find next position in which color will be changed. To do this after each update you should place number i in vertex v and get maximum number in subtree of u, this will give you color of u. And finally you should keep array up_toi in which for color i you will keep first vertex in which path of this color from its initial vertex to the root was interrupted.
You will take only  amortized steps to get to the root when you update colors of vertices and spend
amortized steps to get to the root when you update colors of vertices and spend  operations per each vertex thus complexity still will be
operations per each vertex thus complexity still will be  amortized but you don't have to use any heavy stuff like link-cut trees or heavy-light decomposition.
amortized but you don't have to use any heavy stuff like link-cut trees or heavy-light decomposition.
What, you ask why we will only take  steps to get to the root? Well, I lied a bit when I said that you're not going to use heavy-light decomposition. We will use it to prove this claim. You can do the following thing to recolor vertices. Keep in each light edge stack of colors which lie on its corresponding heavy path. Then when you come into this vertex you will remove some colors which are completely vanished and you will put you current color on top afterwards. Thus on each iteration you will put color in the stack at most
steps to get to the root? Well, I lied a bit when I said that you're not going to use heavy-light decomposition. We will use it to prove this claim. You can do the following thing to recolor vertices. Keep in each light edge stack of colors which lie on its corresponding heavy path. Then when you come into this vertex you will remove some colors which are completely vanished and you will put you current color on top afterwards. Thus on each iteration you will put color in the stack at most  times, which provides amortized estimation for complexity
times, which provides amortized estimation for complexity  of number colors you'll have to change while traveling to the root.
of number colors you'll have to change while traveling to the root.
This all could be done in pretty simple for cycle! (given that you already implemented segment tree and euler tour stuff):
Challenge
Can you improve this solution to  ?
?
Kudos
And now since this blog is recollection of significant part of my experience with string algorithms, I would like to pay some special thanks to people who, probably not even realizing that, made essential contribution in me getting involved with all that beautiful stuff :)
- I_love_natalia, for being that kind of weirdo who accepts friend requests from strangers, and answers ridiculous questions after half-year of silence from them. And for introducing concept of suffix automaton to me of course, since I were too stupid back then (and I am now) to learn things from e-maxx myself and not from other's words :) That's really awesome, most people I know would never waste their time on trying to explain such kind of basic but vast topic in comprehensive manner to literally some random guy from Internet.
- Burunduk1 for this neat gym and great discussions on many algorithmic topics.
- droptable for bringing to me the concept of eertree, it was kind of useful when I had too little understanding of suffix links.
- YuukaKazami for Cyclical Quest. It was somehow the first problem that introduced this kind of stuff with suffix structures to me.
- MinakoKojima for Stringology is Magic. It also was essential in my learning.
- CherryTree for problems Substrings on tree which introduced generic automata on trie to me and Two Strings game which introduced concept of Alice and Bob playing with substrings of particular strings, I was inspired to make two, in my opinion, neat problems after this one. Problems are first and second.
- Radewoosh for calling me his favorite blog writer. I decided to finish this article which was on hold for seven weeks after I read this comment again :D











Gerald03 Editorial
Haha, that's actually a different problem. The one I'm asking about is GERALD3, not GERALD03. And they're really different.
Gerald3 Editorial
My bad. I should see carefully, before posting a link.
.
I want any :)
So, where to find your solution?
.
Interesting! :) How to solve it?
.
Thanks a lot! Will try to implement it :)
I also have one question about palindromes. There is a well-known task about counting the number of different partitions of a given string into palindrome substrings. For example, string "ababa" have 5 different partitions: ababa, aba + b + a, a + bab + a, a + b + aba, a + b + a + b + a
It can be easily solved with simple DP approach where DP[i] = count of partitions for prefix [1..i] in O(N^2) time (N — length of string), and precalculating of all subpalindromes in O(N) time to determine whether any given segment [L,R] is a palindrome or not in O(1), so the total time is still O(N^2) because of DP part. Perhaps, there is a way of solving this task in O(N*log2(N)) or even O(N) using new palindrome technics, that you've been investigating?
.