Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
string s;
cin >> n >> s;
int pos = n - 1;
for (int i = 0; i < n - 1; ++i) {
if (s[i] > s[i + 1]) {
pos = i;
break;
}
}
cout << s.substr(0, pos) + s.substr(pos + 1) << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
long long get(long long n){
for (long long i = 2; i * i <= n; ++i)
if (n % i == 0)
return i;
return n;
}
int main() {
long long n;
scanf("%lld", &n);
long long cnt = 0;
if (n % 2 != 0){
n -= get(n);
++cnt;
}
printf("%lld\n", cnt + n / 2);
return 0;
}
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
typedef long long li;
typedef double ld;
typedef pair<int, int> pt;
li d;
inline bool read() {
if(!(cin >> d))
return false;
return true;
}
inline void solve() {
if(d == 0) {
cout << "Y " << 0.0 << " " << 0.0 << endl;
return;
}
if(d < 4) {
cout << "N" << endl;
return;
}
ld D = sqrt(d * li(d - 4));
ld a = (d + D) / 2.0;
ld b = (d - D) / 2.0;
cout << "Y " << a << " " << b << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
cout << fixed << setprecision(9);
int tc = 1;
assert(cin >> tc);
while(tc--) {
assert(read());
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, pair<int, int> > > g[300043];
int main()
{
int n, m, k;
scanf("%d %d %d", &n, &m, &k);
for(int i = 0; i < m; i++)
{
int x, y, w;
scanf("%d %d %d", &x, &y, &w);
--x;
--y;
g[x].push_back(make_pair(y, make_pair(w, i)));
g[y].push_back(make_pair(x, make_pair(w, i)));
}
set<pair<long long, int> > q;
vector<long long> d(n, (long long)(1e18));
d[0] = 0;
q.insert(make_pair(0, 0));
vector<int> last(n, -1);
int cnt = 0;
vector<int> ans;
while(!q.empty() && cnt < k)
{
auto z = *q.begin();
q.erase(q.begin());
int k = z.second;
if(last[k] != -1)
{
cnt++;
ans.push_back(last[k]);
}
for(auto y : g[k])
{
int to = y.first;
int w = y.second.first;
int idx = y.second.second;
if(d[to] > d[k] + w)
{
q.erase(make_pair(d[to], to));
d[to] = d[k] + w;
last[to] = idx;
q.insert(make_pair(d[to], to));
}
}
}
printf("%d\n", ans.size());
for(auto x : ans) printf("%d ", x + 1);
}
Tutorial
Tutorial is loading...
Solution (Ajosteen)
#include <bits/stdc++.h>
using namespace std;
const int N = int(3e5) + 9;
int n, m;
vector <int> g[N];
vector <pair<int, int> > q[N];
long long add[N];
long long res[N];
void dfs(int v, int pr, int h, long long sum){
for(auto p : q[v]){
int l = h, r = h + p.first;
add[l] += p.second;
if(r + 1 < N) add[r + 1] -= p.second;
}
sum += add[h];
res[v] = sum;
for(auto to : g[v])
if(to != pr)
dfs(to, v, h + 1, sum);
for(auto p : q[v]){
int l = h, r = h + p.first;
add[l] -= p.second;
if(r + 1 < N) add[r + 1] += p.second;
}
}
int main() {
// freopen("input.txt", "r", stdin);
scanf("%d", &n);
for(int i = 0; i < n - 1; ++i){
int u, v;
scanf("%d %d", &u, &v);
--u, --v;
g[u].push_back(v);
g[v].push_back(u);
}
scanf("%d", &m);
for(int i = 0; i < m; ++i){
int v, h, d;
scanf("%d %d %d", &v, &h, &d);
--v;
q[v].push_back(make_pair(h, d));
}
dfs(0, 0, 0, 0);
for(int i = 0; i < n; ++i)
printf("%lld ", res[i]);
puts("");
return 0;
}
1076F - Summer Practice Report
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
typedef long long li;
const int N = 300 * 1000 + 13;
const int INF = 1e9;
int dp[N][2];
int n, k;
int a[N], b[N];
int get(int pa, int pb, int a, int b){
int ans = INF;
if (pa <= k){
int tot = pa + a;
int cnt = (tot + k - 1) / k - 1;
if (b == cnt)
ans = min(ans, tot - cnt * k);
else if (b > cnt && b <= a * li(k))
ans = min(ans, 1);
}
if (pb <= k){
int cnt = (a + k - 1) / k - 1;
if (b == cnt)
ans = min(ans, a - cnt * k);
else if (b > cnt && b <= (a - 1) * li(k) + (k - pb))
ans = min(ans, 1);
}
return ans;
}
int main() {
scanf("%d%d", &n, &k);
forn(i, n) scanf("%d", &a[i]);
forn(i, n) scanf("%d", &b[i]);
forn(i, N) forn(j, 2) dp[i][j] = INF;
dp[0][0] = 0;
dp[0][1] = 0;
forn(i, n){
dp[i + 1][0] = get(dp[i][0], dp[i][1], a[i], b[i]);
dp[i + 1][1] = get(dp[i][1], dp[i][0], b[i], a[i]);
}
puts(dp[n][0] <= k || dp[n][1] <= k ? "YES" : "NO");
return 0;
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 200043;
typedef long long li;
int n, m;
li a[N];
int q;
int f[N * 4];
vector<int> T[4 * N];
vector<int> T2[4 * N];
int mask;
int cur;
vector<int> combine(const vector<int>& a, const vector<int>& b)
{
vector<int> c(1 << m);
for(int i = 0; i < (1 << m); i++)
c[i] = b[a[i]];
return c;
}
vector<int> init(li x)
{
vector<int> ans(1 << m);
for(int i = 0; i < (1 << m); i++)
{
if(i != mask || (x & 1) == 0)
ans[i] = ((i << 1) & mask) ^ 1;
else
ans[i] = ((i << 1) & mask);
}
return ans;
}
void upd(int v)
{
T[v] = combine(T[v * 2 + 2], T[v * 2 + 1]);
T2[v] = combine(T2[v * 2 + 2], T2[v * 2 + 1]);
}
void build(int v, int l, int r)
{
if(l == r - 1)
{
T[v] = init(a[l]);
T2[v] = init(a[l] ^ 1);
return;
}
int m = (l + r) >> 1;
build(v * 2 + 1, l, m);
build(v * 2 + 2, m, r);
upd(v);
}
void push(int v, int l, int r)
{
if(f[v])
{
swap(T[v], T2[v]);
if(l != r - 1)
{
f[v * 2 + 1] ^= 1;
f[v * 2 + 2] ^= 1;
}
f[v] = 0;
}
}
vector<int> id;
void get(int v, int l, int r, int L, int R)
{
push(v, l, r);
if(L >= R)
return;
if(l == L && r == R)
{
cur = T[v][cur];
}
else
{
int m = (l + r) >> 1;
get(v * 2 + 2, m, r, max(L, m), R);
get(v * 2 + 1, l, m, L, min(R, m));
upd(v);
}
}
void add(int v, int l, int r, int L, int R)
{
push(v, l, r);
if(L >= R)
return;
if(l == L && r == R)
{
f[v] ^= 1;
push(v, l, r);
return;
}
else
{
int m = (l + r) >> 1;
add(v * 2 + 1, l, m, L, min(R, m));
add(v * 2 + 2, m, r, max(L, m), R);
upd(v);
}
}
int main()
{
scanf("%d %d %d", &n, &m, &q);
mask = (1 << m) - 1;
for(int i = 0; i < (1 << m); i++)
id.push_back(i);
for(int i = 0; i < n; i++)
scanf("%lld", &a[i]);
build(0, 0, n);
for(int i = 0; i < q; i++)
{
int t, l, r;
scanf("%d %d %d", &t, &l, &r);
--l;
if(t == 1)
{
li d;
scanf("%lld", &d);
if(d & 1)
add(0, 0, n, l, r);
}
else
{
cur = mask;
get(0, 0, n, l, r);
if((cur & 1) == 1)
puts("1");
else
puts("2");
}
}
}










My solution to problem E:
first for each depth sort all vertices by starting time and for each query and vertex U with starting time between starting time V and finishing time V, we add x to ans U (by partial sum, ask in reply for more information). then for all vertex U with starting time between starting time V and finishing time V, in depth height[v] + d + 1, we subtract ans[U] by x (by partial sum). and after all queries we run a dfs and find ans for each vertex.
Fun to see someone that used the same idea (:
I know it's quite old comment but still
(by partial sum, ask in reply for more information)please explain the partial sum approach. ThanksThe problem E can be solved with complexity O(N + M) without sorting or any trees by the next way. We can remember all queries for each vertex V as pairs (X, D), which mean we have to add X to all such vertexes U in the subtree of V that the distance between U and V isn't greater than D. Then we can do DFS.
Let ANS be the current answer. Also we have to get an array CHANGE meaning that when we visit a vertex V we have to decrease ANS by CHANGE[depth[V]], where (obviously) depth[V] means depth of V. So when we visit a vertex V, for each pair (mentioned above) in V we have to increase ANS by X. Also we have to add X to CHANGE[depth[v] + D + 1].
And we must decrease ANS by CHANGE[depth[V]] once. So answer[V] = ANS. When we leave V, we must undo all changes we did in this vertex.
That's all. (I hope, I was clear).
Thanks, your strategy worked perfectly for me.
I realized this problem is basically a generalization of a problem for arrays where one begins with $$$a[\cdot]$$$ all zeros, and receives updates of the form $$$(l,r,x)$$$ meaning $$$a[k]+=x$$$ for every $$$l \leq k \leq r$$$, and after all updates, one needs to recover the array $$$a[]$$$. One could use segment trees for a $$$n \log n$$$ solution, but as in this case it is overkill because queries occur after all updates. (for future readers, the linear time solution for the array problem is to keep an extra array $$$change[\cdot]$$$ with the operation $$$change[l] += x$$$ and $$$change[r+1] -= x$$$ for every update)
I cant understand this implementation for D.
How does he erases something from the set q berfore adding it?
Thanks i just learnt that it is valid to do so.
Why does the following implementation for problem D is giving TLE in TC 67 (I have followed the idea given in editorial) . Here is my implementation [CODE]
It's because you used Java.
On the serious side though, it's because in dijkstra, you need to ignore the node if you've already visited it. Add a line like
if (vis[p.st]) continue;.This thing gave me TLE in C++ too.
sorry for my english but in problem D, according to your algorithm, asume that we need to find the shortest path from vetex 1 to all the others, so we just need n — 1 edges and from that n — 1 edges, we can get all the shortest path from 1, right ? (It just like MST, in MST we need n — 1 edges to get MST, but now, we also need n — 1 edge to get all the shortest path from 1 to another vetex)
Yes. The tree we are building this way is called shortest path tree. In fact, Prim's algorithm of building MST and Dijkstra's algorithm of finding shortest paths are really similar, so we can use the tree built by Dijkstra's algorithm to store all shortest paths.
can anyone help me to figure out what's wrong with my code problem 1076D — Edge Deletion https://codeforces.com/contest/1076/submission/45743114
Suppose there are two edges like (1, 21) and (12, 1). toString(u) + toString(v) will return a string "121" in both cases, so there is a collision. Maybe adding a delimeter or using a pair of ints instead of a string will help.
thanks for the help
About G: It turns out that it can be reduced to O(m(n+q)logn) if we will use the distance to closest losing state instead of a mask of winning and losing states.
I don't know how to maintain the status by this method. Can anyone explain this?
Well, in my solution I consider all possible masks of next m states of dynamic programming. As far as I understood some participants' solutions, they use the fact that only the next winning state matters, so, for example, masks like 01001 and 01000 are exactly the same and can be represented as 01xxx. So we may consider m + 1 different situations: m for every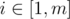 considering the distance to the next winning state, and an extra situation when the next winning state is too far away to be reached.
considering the distance to the next winning state, and an extra situation when the next winning state is too far away to be reached.
Maybe Anadi can explain this idea better.
In my solution I want to know for every position i — can I win if I start in this position. Let's say that if I can win then this position is good. I say that if ai ≡ 0 mod 2 then position i is good. Why? Because if there is a position j such that it is not good then I can move to it, otherwise I can stay in the same position and my opponent has to choose a winning position for me.
Using this fact we can easily solve this task in O(nq) — we pick last position for which we don't know answer, if it's even then it's good, otherwise it's bad and we can mark previous m positions as good.
We can simulate this process faster if we divide out array into blocks of size so final complexity is
so final complexity is 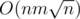 . It was possible to solve it faster in
. It was possible to solve it faster in 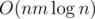 with segment tree (it's practically the same as model solution).
with segment tree (it's practically the same as model solution).
Thanks for the help:) I think I've understood
What does the last array in the code for problem D do? Thanks
This array maintains the index of the last edge on the shortest path from 1 to every other vertex.
awoo There's a typo in the editorial of problem F. The following 2 lines are the correct ones.
1) ... the smallest number of separators you can have is ...
...
2) ... The smallest number of separators is ...
...
The expressions used in code, however, is correct.
Whoops, sure. Fixed, should be ok in a couple of minutes.
How to solve problem E(Vasya and a Tree) for online queries?
Why this: 1+(n−d)/2 for Problem B?
Let d be the initial smallest prime divisor for n.
After finding d, we subtract it, so we have done 1 operation total.
Now, n-d (n after subtracting d) is guaranteed to be even, so for each subsequent operation we will always find 2 and subtract it. We will do (n-d)/2 operations like this.
So we do 1 + (n-d)/2 operations total.
Why is n-d always guaranteed to be even? There are two cases:
1) n is even. So d is even. So n-d is even because even-even=even.
2) n is odd. So d cannot be 2 and 2 is the only even prime number. So d is odd. So n-d is even because odd-odd=even.
In problem C, how do we get a, b = (d±√D) / 2?
This is just the quadratic formula.
For Problem C I tried using a binary search solution. Link: https://codeforces.com/contest/1076/submission/46646184
I'm doing binary search from 0 to d. I take the mid element as a and find b = d — a. To break out of the binary search I check if a*b == d and return a or if mid becomes equal to either a or b (I figured they might after one point because of precision) in which case I return -1 indicating it is not possible.
This is not working for all test cases and I think it's off by some precision cause it isn't passing the sample. What is the correct way to do this if it were to be done using binary search?
Help required in problem 1076D-Edge Deletion. http://codeforces.com/contest/1076/submission/59660020
What I am doing is over here is,first find the MST of the given graph. And then run a dfs on this MST and keep adding edges until the count is less than k. What is wrong with this approach??
test case (format as of problem first number is vertices in graph , 2nd is edges , k , then edges description) 3 3 2 1 2 2 2 3 1 1 3 2 Draw MST and see the difference for vertex 3 , shortest distance via mst approach will be 3 unit , but if you just considered simple edge of 1-2 and 1-3 , shortest path to vertex 3 will be 2 unit. Hence mst may cause problems , better to use dijkstra from single source.
I learnt a lot from Problem E. Thanks.