I have learnt from this site that n! modulo p where p is a prime, can be calculated using Wilson's Theorem and FFT with complexity sqrt(p).(log p)^3
There is also a problem using the idea in SPOJ. link
But I am not being able to implement the idea. If anyone have any implementation of the problem please feel free to share.
Thanks for your time. Happy Coding.










It has many parts. Try implementing / debugging one part at a time maybe?
First part is calculating (x + 1)(x + 2)...(x + m). Try this here: 960G - Bandit Blues
The later one is the harder part: Multipoint Evaluation. You can try submitting here: POLYEVAL -Evaluate the polynomial. It has weak judge data that allows sub optimal solutions.
Again, for that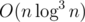 multipoint evaluation you need polynomial inverse. You can test that here: 438E - The Child and Binary Tree (which also needs square root of a polynomial, also has good editorial on how to do that).
multipoint evaluation you need polynomial inverse. You can test that here: 438E - The Child and Binary Tree (which also needs square root of a polynomial, also has good editorial on how to do that).
If you don't know how multipoint evaluation is done, read this: On Fast Fourier Transform
Hmmm, but multipoint evaluation is , isn't it?
, isn't it?
Oh, yes. I mixed it with Interpolation.
Your approach could be improved to , where
, where 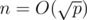 .
.
That is, if you want to calculate fn(d), fn(2d), ..., fn(nd) where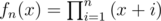 , you may calculate fn / 2(d), fn / 2(2d), ..., fn / 2(nd / 2) first, use FFT and binomial coefficient to calculate fn / 2((n / 2 + 1)d), fn / 2((n / 2 + 2)d), ..., fn / 2(nd), fn / 2(d + n / 2), fn / 2(2d + n / 2), ..., fn / 2(nd + n / 2) then, and finally obtain fn(x) by fn / 2(x)·fn / 2(x + n / 2).
, you may calculate fn / 2(d), fn / 2(2d), ..., fn / 2(nd / 2) first, use FFT and binomial coefficient to calculate fn / 2((n / 2 + 1)d), fn / 2((n / 2 + 2)d), ..., fn / 2(nd), fn / 2(d + n / 2), fn / 2(2d + n / 2), ..., fn / 2(nd + n / 2) then, and finally obtain fn(x) by fn / 2(x)·fn / 2(x + n / 2).
If you need more details, please refer to 階乗 mod 素数 — Min_25's memo.
Relatedly, this is also how you get the fastest (in terms of asymptotics) deterministic integer factorization algorithm: if n is a composite it has a prime factor that is at most n1 / 2, so compute ⌈ n1 / 2⌉! modulo n in O(n1 / 4polylog(n)) time and take the GCD of the result with n.
With competitive programming (1 sec TL) point of view, isn't it worse than the simple O(root(N)) factorisation?
I have no idea how fast it is in practice, but yea, it's probably not very useful in a competitive programming context :-)
If modulo is not fixed then you can't apply it.
What do you mean?
About Slow_But_Determined approach not yours.
Wait, I was talking about the brute-force factorisation method which does not even need any modulo :/
Mainly for future reference: There's also a solution in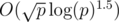 that uses generating functions to efficiently evaluate a polynomial of degree d at {0, 2k, 2·2k, 3·2k, ..., (m - 1)·2k} in
that uses generating functions to efficiently evaluate a polynomial of degree d at {0, 2k, 2·2k, 3·2k, ..., (m - 1)·2k} in 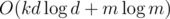 .
.
Let f be a polynomial of degree d, then the sequence (an)n defined by an = f(n) satisfies a linear recurrence with characteristic polynomial (X - 1)d + 1. From this, we get a generating function
where P0 is a polynomial of degree at most d + 1 that can be computed by
We extend the left side by (X + 1)d + 1 and get
If we decompose the numerator into even and odd terms and let P1(X2) denote the even terms of the numerator, then we get by considering only even terms
i.e.
so we found a generating function for f(0), f(2), f(4), .... By repeditively defining
we get generating functions
so we can compute the first m terms on the left by power series inversion.
If we want to compute N!, then we pick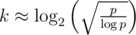 , let
, let 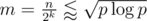 , take
, take
with d = 2k and initial values
and use the above algorithm to compute F(2k), F(2·2k), ..., F(m·2k). Then multiply the results together with the numbers from m2k + 1 to N. The total runtime is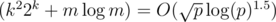 .
.
Can you share your implementation of this problem from SPOJ as I am not able to implement my own. I saw that you got AC for this Factmodp problem on Spoj.