SPOILER ALERT: Please do not read these hints if you want to solve some problems in this contest but haven't attempted yet.
Hints are categorized by the number of accepted teams.
102028A - Xu Xiake in Henan Province
Read and implement.
102028D - Keiichi Tsuchiya the Drift King
There are only two cases, so just draw them on draft paper.
102028E - Resistors in Parallel
The resistance of the n-th section is a multiplicative function of n, which only depends on distinct prime factors.
BFS is enough.
Be careful with leading whitespaces and too many test cases.
Picking half of points from every boundary is enough.
102028B - Ultraman vs. Aodzilla and Bodzilla
Let f(n) be the minimal integer t such that 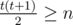 .
.
If the first died monster has p health points and the second one has q, the best strategy should lead the former one to die at f(p)-th second and lead the latter one to die at f(p + q)-th second.
The rest is just to enumerate which one should die firstly, and construct the lexicographical smallest strategy greedily.
Be careful when the received damages are equal in these two cases.
One observation is that coordinates of rooks in each type form a permutation.
If split the area into 9 grid regions, one can find rooks can only collide in at most 4 regions.
Coordinates are easy to maintain as well.
102028H - Can You Solve the Harder Problem?
Suffix structures may help counting distinct contiguous subsequences (intervals).
Segment tree (or fenwick tree) with stack may help maintaining maximum values of intervals offline.
102028G - Shortest Paths on Random Forests
Let f(n) be the number of labelled forests having n vertices, g(n) be the number of pairs of reachable vertices in labelled forests having n vertices, and h(n) be the sum of lengths of the shortest path between every pair of reachable vertices in labelled forests having n vertices.
Calculating f(n) is typical: Enumerate the size of component containing label 1, and conclude 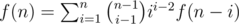 . Speed it up by divide and conquer (or Newton iteration).
. Speed it up by divide and conquer (or Newton iteration).
For g(n), one can conclude 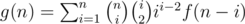 by enumerating contributions of each component.
by enumerating contributions of each component.
For h(n), it can be reduced into counting the number of ways to pick k ordered edges on the shorest path between every ordered pair of vertices (k = 1, 2). Imagine these k edges split a component (tree) into (k + 1) components (trees), and one can conclude calculating the number of ways is equivalent to calulcate the (k + 1)-th power of the polynoimial 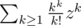 .
.
There are two cases which depend on if carpets intersect, so we need to know the number of squares covered by exact k carpets (k = 1, 2).
It is easy to show the number of useful pairs of 2 carpets is at most m2, so the difficulty of this problem is only counting the number of squares covered by exact k carpets.
Sweep line with segment tree can do this in 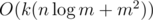 , while maintaining some statistics obtained from 2-dimensional partial sum and solving equations for each square can do this in O(k(n + m2)).
, while maintaining some statistics obtained from 2-dimensional partial sum and solving equations for each square can do this in O(k(n + m2)).
102028K - Counting Failures on a Trie
One can easily determine if a substring forms a matching path starting from node 0 by binary search with hashing, so for each left endpoint, one can find the mismatched right endpoint quickly.
Then for each query, binary lifting could speed up the process of failed matching.
There are 5 types of connected subgraphs, one can count them using inclusion-exclusion principle, which leads to count the number of k-cycles in the graph (k = 3, 4).
One can solve the typical counting problem in 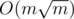 .
.











For problem K, though solutions are accepted, there exist some solutions in
solutions are accepted, there exist some solutions in  .
.
One observation is that what we need to do is to match the suffix tree of S with the trie.
Assuming suffixes of string S are sorted in lexicographical order, one can observe that each node in the trie can match a contiguous subsequence of sorted suffixes.
Thus, using binary search to match a single character with these suffixes is enough, which does not require hashing.
For problem L, how to count the number of 4-cycles in such time complexity?
Let's sort vertices in degree non-ascending order and relabel them, that is, if u is the i-th element after the sort, we relabel it as i.
We may enumerate a, b, c, d ranged from 1 to n and check if a - b - c - d - a form a 4-cycle when a = min(a, b, c, d) and b < d. It is easy to show, for each simple 4-cycle, it will be counted exactly once.
Actually, we can just enumerate 3 vertices to accomplish the mission. Let's set a counter cnt(w) for each vertex w. And then, do the following algorithm:
Do you notice that v can be less or greater than x but each 4-cycle is still counted exactly once?Analysis of time complexity:
Does the aforementioned algorithm really need a threshold T?Btw, you need to store the graph using something like
std::vector, otherwise the cache missing will lead to TLE like my code.Actually, f(T) = m * T + 2 * m * 2 * m / T >= 2 * sqrt(m * T * 2 * m * 2 * m / T) = 4 * m * sqrt(M) from AM >= GM inequality and in AM-GM we have equality when terms are equal so T = 2 * sqrt(M). Complexity is still the same, but if you want to be mathematically accurate, T = 2 * sqrt(M) is the right value.
How to solve problem E (Resistors in Parallel)?
for the given Input:
am I missing something?
r8 = ∞ because 22|8. And consequently, the resistance of S8 should be , which is equal to the resistance of S2k for k = 1, 2, ....
, which is equal to the resistance of S2k for k = 1, 2, ....
sorry, my bad! how should i proceed with this since the numbers are really large (100 digit number) and couldn't find any relation with the given hint(finding prime factors would also timeout)?
With the hint, the remaining is a problem about the constructive algorithm. Try to avoid the factorization. GL!
The time limit of L seems too tight? I tried various ways of optimization (including
fread-based input) and finally get AC in around 11.2 sec / 12.0 sec...ps. My AC code
How do you prove that the greedy solution is correct in B?