Tutorial
Tutorial is loading...
Solution (BledDest)
q = int(input())
for i in range(q):
l, r, d = map(int, input().split())
if(d < l or d > r):
print(d)
else:
print((r // d) * d + d)
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
void rem(string &s, const string &c) {
auto pos = s.find(c);
if (pos == string::npos) {
cout << -1 << endl;
exit(0);
}
s.erase(0, pos + 1);
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
string s;
cin >> s;
rem(s, "[");
rem(s, ":");
reverse(s.begin(), s.end());
rem(s, "]");
rem(s, ":");
cout << count(s.begin(), s.end(), '|') + 4 << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> pt;
int n;
vector< pair<pt, int> > segs;
inline bool read() {
if(!(cin >> n))
return false;
segs.resize(n);
for(int i = 0; i < n; i++) {
cin >> segs[i].x.x >> segs[i].x.y;
segs[i].y = i;
}
return true;
}
bool cmp(const pair<pt, int> &a, const pair<pt, int> &b) {
if(a.x.y != b.x.y)
return a.x.y < b.x.y;
if(a.x.x != b.x.x)
return a.x.x < b.x.x;
return a.y < b.y;
}
inline void solve() {
sort(segs.begin(), segs.end(), cmp);
int mn = segs[n - 1].x.x;
for(int i = n - 2; i >= 0; i--) {
if(segs[i].x.y < mn) {
vector<int> ts(n, 2);
for(int id = 0; id <= i; id++)
ts[segs[id].y] = 1;
for(int t : ts)
cout << t << ' ';
cout << '\n';
return;
}
mn = min(mn, segs[i].x.x);
}
cout << -1 << '\n';
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
int tc;
cin >> tc;
while(tc--) {
assert(read());
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define mp make_pair
#define pb push_back
#define sqr(a) ((a) * (a))
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define forn(i, n) for(int i = 0; i < int(n); i++)
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template <class A, class B> ostream& operator << (ostream& out, const pair<A, B> &a) {
return out << "(" << a.x << ", " << a.y << ")";
}
template <class A> ostream& operator << (ostream& out, const vector<A> &v) {
out << "[";
forn(i, sz(v)) {
if(i) out << ", ";
out << v[i];
}
return out << "]";
}
mt19937 rnd(time(NULL));
const int INF = int(1e9);
const li INF64 = li(1e18);
const int MOD = INF + 7;
const ld EPS = 1e-9;
const ld PI = acos(-1.0);
const int N = 200 * 1000 + 13;
int n;
int a[N];
vector<int> g[N];
bool read () {
if (scanf("%d", &n) != 1)
return false;
forn(i, n)
g[i].clear();
forn(i, n)
scanf("%d", &a[i]);
forn(i, n - 1){
int x, y;
scanf("%d%d", &x, &y);
--x, --y;
g[x].pb(y);
g[y].pb(x);
}
return true;
}
vector<pt> dp[N];
int ans;
void calc(int v, int p = -1){
vector<pt> chd;
for (auto u : g[v]) if (u != p){
calc(u, v);
for (auto it : dp[u])
chd.pb(it);
}
sort(all(chd));
forn(i, sz(chd)){
int j = i - 1;
int mx1 = 0, mx2 = 0;
while (j + 1 < sz(chd) && chd[j + 1].x == chd[i].x){
++j;
if (chd[j].y >= mx1)
mx2 = mx1, mx1 = chd[j].y;
else if (chd[j].y > mx2)
mx2 = chd[j].y;
}
if (a[v] % chd[i].x == 0){
ans = max(ans, mx1 + mx2 + 1);
dp[v].pb(mp(chd[i].x, mx1 + 1));
while (a[v] % chd[i].x == 0)
a[v] /= chd[i].x;
}
else{
ans = max(ans, mx1);
}
i = j;
}
for (int i = 2; i * i <= a[v]; ++i) if (a[v] % i == 0){
dp[v].pb(mp(i, 1));
ans = max(ans, 1);
while (a[v] % i == 0)
a[v] /= i;
}
if (a[v] > 1){
dp[v].pb(mp(a[v], 1));
ans = max(ans, 1);
}
}
void solve() {
forn(i, N) dp[i].clear();
ans = 0;
calc(0);
printf("%d\n", ans);
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
int tt = clock();
#endif
cerr.precision(15);
cout.precision(15);
cerr << fixed;
cout << fixed;
#ifdef _DEBUG
while(read()) {
#else
if (read()){
#endif
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
int main() {
int n;
scanf("%d", &n);
int mxa = 0, mxb = 0;
static char buf[5];
forn(i, n){
int x, y;
scanf("%s%d%d", buf, &x, &y);
if (x < y)
swap(x, y);
if (buf[0] == '+'){
mxa = max(mxa, x);
mxb = max(mxb, y);
}
else{
puts(mxa <= x && mxb <= y ? "YES" : "NO");
}
}
}
Tutorial
Tutorial is loading...
Solution 1 (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define all(a) (a).begin(), (a).end()
#define mp make_pair
#define pb push_back
#define x first
#define y second
typedef long long li;
typedef pair<int, int> pt;
const int INF = int(1e9);
const int N = 411;
int n, m;
int a[N];
vector< pair<pt, pt> > qs;
inline bool read() {
if(!(cin >> n >> m))
return false;
fore(i, 0, n)
cin >> a[i];
qs.resize(m);
fore(i, 0, m) {
cin >> qs[i].x.x >> qs[i].x.y >> qs[i].y.x >> qs[i].y.y;
qs[i].x.x--; qs[i].x.y--;
}
return true;
}
vector<int> ids[N];
int d[N][N];
inline void solve() {
fore(i, 0, m)
ids[qs[i].x.x].push_back(i);
li ans = -1;
fore(l, 0, n) {
fore(r, l, n)
d[0][r] = a[r] - a[l];
fore(k, 1, n + 1) {
int opt = l;
fore(r, l, n) {
while(opt < r && max(d[k - 1][opt], a[r] - a[opt]) >= max(d[k - 1][opt + 1], a[r] - a[opt + 1]))
opt++;
d[k][r] = max(d[k - 1][opt], a[r] - a[opt]);
}
}
for(int id : ids[l])
ans = max(ans, d[qs[id].y.y][qs[id].x.y] * 1ll * qs[id].y.x);
}
cout << ans << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
if(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Solution 2 (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define all(a) (a).begin(), (a).end()
#define mp make_pair
#define pb push_back
#define x first
#define y second
typedef long long li;
typedef pair<int, int> pt;
const int INF = int(1e9);
const li INF64 = li(1e18);
const int N = 411;
int n, m;
int a[N];
vector< pair<pt, pt> > qs;
inline bool read() {
if(!(cin >> n >> m))
return false;
fore(i, 0, n)
cin >> a[i];
qs.resize(m);
fore(i, 0, m) {
cin >> qs[i].x.x >> qs[i].x.y >> qs[i].y.x >> qs[i].y.y;
qs[i].x.x--; qs[i].x.y--;
}
return true;
}
int getCnt(const pair<pt, pt> &q, li mx) {
li dist = mx / q.y.x;
int s = q.x.x, f = q.x.y;
int u = s, cnt = 0;
while(u < f) {
int v = u;
while(v < f && a[v + 1] - a[u] <= dist)
v++;
if(v == u)
return INF;
cnt++;
u = v;
}
return cnt - 1;
}
li upd(const pair<pt, pt> &q, li lf, li rg) {
if(getCnt(q, lf) <= q.y.y)
return lf;
while(rg - lf > 1) {
li mid = (lf + rg) >> 1;
(getCnt(q, mid) <= q.y.y ? rg : lf) = mid;
}
return rg;
}
inline unsigned int getHash(const vector<int> &vals) {
unsigned int hash = 0;
for(int v : vals)
hash = hash * 3 + v;
return hash;
}
inline void solve() {
auto seed = getHash(vector<int>(a, a + n));
fore(i, 0, m)
seed = seed * 3 + getHash({qs[i].x.x, qs[i].x.y, qs[i].y.x, qs[i].y.y});
mt19937 rnd(seed);
vector<int> ids(m, 0);
iota(all(ids), 0);
shuffle(all(ids), rnd);
li curv = 0;
for(int id : ids)
curv = upd(qs[id], curv, 2 * INF64);
cout << curv << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
if(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
1101G - (Zero XOR Subset)-less
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 200 * 1000 + 13;
const int LOGN = 30;
int n;
int a[N], pr[N];
int base[LOGN];
void try_gauss(int v){
for(int i = LOGN - 1; i >= 0; i--)
if (base[i] != -1 && (v & (1 << i)))
v ^= base[i];
if (v == 0)
return;
for(int i = LOGN - 1; i >= 0; i--) if (v & (1 << i)){
base[i] = v;
return;
}
}
int main() {
scanf("%d", &n);
forn(i, n)
scanf("%d", &a[i]);
memset(base, -1, sizeof(base));
forn(i, n){
pr[i + 1] = pr[i] ^ a[i];
try_gauss(pr[i + 1]);
}
if (pr[n] == 0){
puts("-1");
return 0;
}
int siz = 0;
forn(i, LOGN)
siz += (base[i] != -1);
printf("%d\n", siz);
}










Help in C
If we've found such ri then all prefix goes to one group and suffix — to another. ??
look at it in this way... if we have such an ri.. then that means all the segments that lie on the right side of current index have their l and r greater than ri... and all the segments before have their l and r <= current ri.. so ri can work as a boundary point where every thing on left can go to one set and everything on right go to the other.
I am totally not understand the solution of problem G, can anyone help me ? :(((
Your proof of the solution of problem G suggests that one can do something a little bit simpler.
Just write all the numbers in base 2 and put them as rows of a matrix (the order doesn't matter). Then the answer is just the rank of that matrix. Of course, the corner case has to be taken into account, i.e. if the xor of all numbers equals zero, then the answer is -1.
Oh, I agree! Of thought of prefix XORs for so long that I missed the thing the prefix XOR is a linear combination of the numbers in it itself.
I don't care if this is downvoted but Problem D editorial is not properly written.
Problems with the editorial in D.
1. " Let's for each v calculate the path of the maximum length to pass through it "
It does not say why are we calculating it and where are we using this.
2. The last paragraph seems to be the heart of algorithm and it is written in just two lines without much explanation.
3. The code uses dp to store something but the editorial doesn't mention anything about it and so for someone who is reading through the code how the hell are we supposed to know what is dp[i].
4. The code is not properly commented.
I don't know if the author write editorial for those who already know how to solve the problem. CF editorials are fast, which is great but they need a more of detailing.
Apart from this the contest and problems were great!
Lastly can anybody explain the solution for problem D?:p
Sure, the solution must be detailed for people with low rating like me, because its an educational round.
Thirst of all it should contained the definitions of tree. That is the difference between tree from this task and graph. What is the the simple path (probably some pictures will help me)?
Every time I'm solving Codeforces contest dynamic or graph tasks stopped me. Please help or Ill never have progress here.
Thirst of all it should contained the definitions of tree. That is the difference between tree from this task and graph. What is the the simple path.
All I am saying is the editorial should be such that the main algorithm used to solve the problem should be properly conveyed to the audience(and thus more detailing of that is required) and not the things you are talking about.
I agree I failed at explaining the solution and I'm sorry for it.
I genuinely tried to cover the parts that I believe to matter to the solution. I prefer to think of included code as a reference to one of the possible implementations of editorial, not the only one of the kind. The part with two pointers and such definitely takes the most number of lines in my code, but no way it's the most important. Like you don't even have to do two pointers over there, there are multiple ways to update the answer with the array of values for children.
The editorial, though, came out to be understandable only for those who have already coded the similar things, whoops.
Here is my approach to problem D (Although I did a silly mistake during contest but was able to solve after the contest)
Firstly I rooted the tree at 1st node (you can root it at any node). I kept a map for every node which denotes the following —
dp[u][gcd] = dist, wheredistis maximum distance possible in a path that starts with a node that is in subtree ofuand ends at nodeuand the gcd of the path isgcd.How to calculate this?
This can be done using dfs. Initially for every node put
dp[u][a[u]] = 1if a[u] is not 1. Then do the following —Why do we need this?
For each node
uwe have two options -dp[x][g1] = dist1anddp[y][g2] = dist2andgcd(g1, g2, a[u]) != 1,ans = max(ans, dist1 + dist2 + 1)This can be also incorporated in the same dfs as follows —
The trick is that when we are visiting i'th child, the ans upto (i — 1)'th child would already be included in the parent's dp and could be used.
Awesome, I don't get why this isn't the tutorial for problem D. It is way more understandable
Awesome tutorial __naruto__!
I think there is a minor error in the code in the if condition ( if(_gcd(a[v], a[u]) != -1)_ ) shouldn't it be if(_gcd(a[v], a[u]) != 1)_ in the second code.
Thanks Ghost0fSparta, Edited!
__naruto__ would you plz explain the complexity. Its not quite obvious.
Doesn't your algo consume O(n^2) space?
No because the no. of possible GCDs for each vertex varies but I don't know what is the upperbound for same
What is the time complexity of this algorithm ? How many times the inner loop will run for each vertex ? Also, how can we estimate the average size of dp[u] for each vertex ie. what will be the rough count of gcd for given vertex / overall size of map?
Hmm, let's try this one more time but with references to the code. The code contains:
dp[v] — the vector of the pairs (p, len) — the length of the maximum path that goes through v such that all numbers on it is divisible by p; calc(v) — dfs to calc children before the parent.
After I calculate dp[u] for all children u of v, I take all these vectors and merge them into a single vector chd. I'll use it now to update the answer. Let's look into two kinds of paths to go thorough v:
And the final part is calculating dp[v]. Take all chd pairs and extend the possible ones to v. If some primes of a[v] were not included in there, push pairs (p, 1) for them.
Bonus for G: Prove that answer doesn't change if we permute elements of array a.
Why is this downvoted?) It isn't that obvious from the editorial and jury's solution as well.
Any prefix can be represented as xors of elements of a, and any element in a can be represented as pre[i]^pre[i+1], so the array of prefix actually contains the same number of basis as array a, thereby the answer should be the same.
Since awoo says so, I'll explain the model solution for D.
What does it mean that the greatest common divisor of some set of numbers is not 1? It means that there exists some prime number p that divides the greatest common divisor. Therefore, it divides all the numbers in a set. Okay, now we can fix some prime number p, find the best path that passes only through vertices with ai divisible by p, then fix another prime, and check all the primes from 2 to 199999 this way.
What happens when we fix a prime number? Basically, the vertices of the graph are now divided into two groups: those that are forbidden to pass through (having ai not divisible by p) and those that are allowed. Let's delete all forbidden vertices from the tree (and all the edges that are incident to at least one forbidden vertex).
What will the resulting graph look like? It might become disconnected (for example, in the first sample case, if we fix p = 2, vertices 1 and 3 are disconnected), but it's still acyclic because removing edges or vertices from a graph won't create a new cycle. So, each connected component of the graph is a tree. Now we have to find the best path in each connected component.
Okay, how to determine the "best" path? If the number of vertices on a path is x, and the path is simple, then the number of edges belonging to this path is x - 1. And since each component is a tree, then we are interested in finding the diameter of the tree, which can be done in O(|V|): pick some vertex from the tree (let's denote it as v0), run DFS or BFS from it, find the vertex having the greatest distance from v0 (let it be v1; if there are muliple such vertices, pick any of them), run DFS or BFS from it, and find some vertex having greatest vertex from v1 (let it be v2). The path between v1 and v2 is the diameter.
Why does it work fast enough? Each number exceeding A can have no more then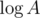 prime divisors, so the sum of sizes of the graphs we are finding the diameters in is bounded as
prime divisors, so the sum of sizes of the graphs we are finding the diameters in is bounded as 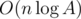 .
.
Okay, how to implement it? When we pick some prime p, instead of deleting forbidden vertices and edges (which leads us to complexity of O(nA) or even greater), let's create a new graph: renumerate all allowed vertices so that their numbers become 1, 2, ..., k, and apply the aforementioned solution to this graph. That is the easiest way to make it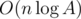 without using some auxiliary sets or other data structures.
without using some auxiliary sets or other data structures.
upd: Well, in fact, model solution is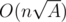 because I was too lazy to write fast factorization algorithms. But it's worth mentioning that if you want to achieve complexity of
because I was too lazy to write fast factorization algorithms. But it's worth mentioning that if you want to achieve complexity of 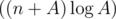 , there's no need to write Eratosthenes sieve: finding all divisors of all numbers from 1 to A in
, there's no need to write Eratosthenes sieve: finding all divisors of all numbers from 1 to A in 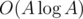 can be done using two nested for loops, the outer one iterating on the divisor, and the inner one iterating on the numbers divisible by that divisor.
can be done using two nested for loops, the outer one iterating on the divisor, and the inner one iterating on the numbers divisible by that divisor.
Can you provide the link to the model solution please?
It lacks some optimizations I explained in the post, and its complexity is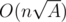 for factorization and
for factorization and  for actually solving the problem. If you are still interested, here it is.
for actually solving the problem. If you are still interested, here it is.
It seems that such a decision.
https://codeforces.com/contest/1101/submission/48393923
Can you please explain the complexity of your code??
I implemented your solution but its giving TLE. Can you please help https://codeforces.com/contest/1101/submission/48648294
Your solution works in because for each prime you check all numbers to find which are divisible by this prime. To improve it, you have to factorize each ai, and for each prime memorize a list of vertices having ai divisible by it — and when choosing a prime, iterate only over those vertices, not over the whole tree.
because for each prime you check all numbers to find which are divisible by this prime. To improve it, you have to factorize each ai, and for each prime memorize a list of vertices having ai divisible by it — and when choosing a prime, iterate only over those vertices, not over the whole tree.
Thank you so much
In C part for the test case 1 4 1 2 2 4 4 8 5 10. the output should be 1 1 1 2 but according to the editorial it's giving -1
[4, 8] and [5, 10] intersect.
Thanks i misinterpreted the question as for segment[ li, ri] i didn't thought it meant range li to ri. BTW what's a good approach to solve the question if instead of segments, sets with discrete value is given. For ex. {1,2,3},{2,3,4},{7,8,9} (ans-1 1 2) .Should i use set_intersection and iterate over all sets?
Build an undirected graph with two types of vertices: vertices representing numbers, and vertices representing sets. Connect all "set"-vertices with corresponding "number"-vertices. Now we have to color this graph into two colors so vertices in the same component share the same color.
I get nothing from task G tutorial, could anyone explain the solution?
Can anyone please explain why opt[l][r][k] <= opt[l][r+1][k] in problem F..?? I am not able to visualize this.
I have a slightly different solution for F. We still calculate dp[l][r][k], and the recurrence is still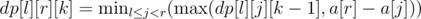 . However, we notice that dp[l][j][k - 1] increases as you increase j, and a[r] - a[j] decreases as you increase j. Thus, the min value of
. However, we notice that dp[l][j][k - 1] increases as you increase j, and a[r] - a[j] decreases as you increase j. Thus, the min value of  will occur when they are as close to each other as possible, i.e. when |dp[l][j][k - 1] - (a[r] - a[j])| is minimized, and this quantity is unimodal so we can binary search for it. For memory optimization, we simply notice that we don't need to store all the queries, and can process them online, giving us O(n3) space rather than O(n3 + q), which barely fits into the memory. The DP calculation takes
will occur when they are as close to each other as possible, i.e. when |dp[l][j][k - 1] - (a[r] - a[j])| is minimized, and this quantity is unimodal so we can binary search for it. For memory optimization, we simply notice that we don't need to store all the queries, and can process them online, giving us O(n3) space rather than O(n3 + q), which barely fits into the memory. The DP calculation takes 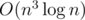 time, which also barely fits into the time limit.
time, which also barely fits into the time limit.
48306162
Can anyone help me in finding mistake in D? I am not able to find why it is giving WA. Submission
Choose your i/o functions wisely.Actually I think a problem shouldn't be annoyed with slow i/o.But you guys should know scanf/printf is faster than cin/cout.When the input is larger than 5MB you should use scanf/printf without hestitation.
(Also the only way to make this simple problem E harder is to hack some slow i/o's...Maybe?)
For problem D, I have used the concept that-For any vertex 'v' it can either be a part of the longest path or not. Then i calculated the longest path in its sub-tree and updated the max value, and then passed the value of the longest path obtained from its children to its parent. But this approach is giving wrong answer on test 5. Here is my code, why isn't this approach working. https://codeforces.com/contest/1101/submission/48279577
Consider this test case :
The answer should be
3but your code outputs2.The problem is with how you are calculating answer. You are returning
maxx+1 and so are never considering the case when the largest path can be through one vertex conncting two nodes of the children whenmaxx>0. Also while calculating theansvariable you are not considering the fact thatsmaxxandmaxxcan be having their gcd = 1(egsmaxx= 3 because of path having gcd = 2 andmaxx= 3 because of path having gcd = 3 and when you say answer = 3+3=6 you are considering a path having gcd(2,3) = 1). There can be more but I think these are the major ones.https://codeforces.com/contest/1101/submission/48316745 well, i am considering the case when the largest path can be through the vertex i am currently on
ans = max(ans,maxx+smax+1). In the last solution i missed to give = inlen>=maxcondition. Heremaxxis the longest path in the subtree of the current vertex andsmaxxis second longest. thats whymaxx+smaxx+1gives the longest path through the current vertex. Regarding your second argument thatgcd(smaxx,maxx)=1. why would i be taking gcd of length of the paths.I didn't mean length of paths, I meant the gcd of all ai s in the path
And it is still giving wrong answer for the test case I provided above.
I have another idea about D but I got WA. Could anybody help me?
I tried to deal with it by DP in trees. Denote dp[i] as a set where stored some pairs (g, d). A pair (g, d) in dp[i] means a path form v to vertex i that the gcd of vertices in the path is g and its length is d, where v is one of the grandsons of vertex i. It's evidently I needn't store the pairs (g, d) where g = 1 and also I can ignore the vertex i where a[i] = 1. And if there are two pairs which have the same g, I can ignore the one with the lower d.
Of course a pair (a[i], 1) is in dp[i] if a[i] > 1. Consider all children of vertex i, assuming that now I'm consider v. Get all pairs in dp[v], assuming that now I get (g0, d0). Insert pair (gcd(g0, a[i]), d0 + 1) to dp[i] and maintain the optimal pairs if gcd(g0, a[i]) > 1, which means vertex i links into the path. However, the answer can be the path from one of the grandsons of vertex i to another. So before the insertion, I consider all pairs in dp[i] to get the potential answer. dp[i] now stores some pairs stand for the path from vertex i to one of the grandsons of vertex u, where vertex u is one of the children which is already considered of vertex i. Assuming that I'm considering pair (g1, d1) in dp[i], ans = max(ans, d0 + d1) if gcd(g0, g1) > 1.
I don't know what's wrong with my approach or my code because of my poor ability. Here's my Submission 48313349. I'd appreciate it if someone help me.
Sorry for my poor English.
It seems, you return from dfs when au = 1. I believe, that best answer might be in a subtree of such a vertex, but you won't reach it.
Oh yes. What a stupid mistake I made! Thanks a lot! :)
But I still got WA. :(
My answer is greater on test 6. Could you help me again? Thanks. 48320981
Try this test
Thank you very much! I knew how to improve my approach. :)
hkjhbkb
The idea of brute is ok, your bfs has a bug in it.
ksjgfisudgc
Hi, Your code is a bit difficult to read, but I've found a testcase, for which you code outputs Wrong Answer. Since Testcase 6 is big, so it would be harder to debug, so try this:
Correct Answer is 3 and your code is outputting 4.
Hope this helps
Thank you very much and sorry for my poor skill.
I know what mistake I've made now. As I insert pairs into dp[i], I may get the two paths from the same child. So I can insert them to another set so that I can't reach them when considering the child. And in the end I insert them into dp[i]. I finally got AC! Thank awoo and atom0410! :)
I just found out my solution for problem D was incorrect . But yet I got AC even after the system test . It happened because of weak test cases .
Test Case # X :
4
3 6 2 2
1 2
2 3
3 4
My Submission :
48253431
The correct answer should be 3 , but my solution is giving 2 .
Can you guys rejudge problem D
I added the test, thanks. We won't rejudge but all the further submissions will be tested on it.
The test cases were very weak.I also saw a solution which was accepted but was giving wrong answer for other testcases. https://codeforces.com/blog/entry/64484
Aha! I love problem F.
I solved this problem by randomization and binary search. The code is easy to read. 48318449
Let us analyze this problem, we know every truck must have the max gas-tanks. For a truck, the more oil, the better.
We randomly choose a truck to calculate ( use binary search ), It can be considered that in general, half of the trucks do not exceed the maximum fuel consumption. In other words, we only use logm operations( binary search) at most.
This is the idea of Blogewoosh #6.
Could you please further explain what your check function does ?
Hey awoo , I am not able to understand that why solution for E getting TLE thought its complexity is O(N), but it is accepted when i used ios::sync_with_stdio(false); cin.tie(0); N <= 500000 Solution ID : https://codeforces.com/contest/1101/submission/48324180 Solution ID (without ios::...) : https://codeforces.com/contest/1101/submission/48324102
And the time limit for Question is 3sec.
Can you help with this, Thanks in advance:)
Because reading from stdin using cin without disabling its synchronization with stdio is slow. Also in some cases its better to use
scanf,printf.Some tests were already made: https://codeforces.com/blog/entry/5217?locale=en
for problem D fix a prime p and find longest path with vertices divisible by p! Consider the vertices divisible by p, there are some disjoint maximal subtree with all vertices divisible by p obviously the longest path is diameter of one of these subtrees. so we will find for each vertex v and prime p as prime factor of v , the diameter of the subtree contains v , it can be done with dp on tree! we have nlogMAXN pair(v,p) and each dfs goes to some of them so in total we visit nlogMAXN state, also to avoid going to each subtree many time we should mark state (v,p) if we use a set the time will be nlog^2(MAXN) or if we use an array of sets reduce it to n*logMAXN*loglogMAXN or if we use hashing it is nlogMAXN! :)
My submission
bro, i solved D using recursion, at each node i m storing the maxdepth for each factor in its subtree, so if a parent node have three child all three child would have been processed before i come to process the parent node and again i will store the same set of variables for parent node and WILL ALSO CHECK(means consider) THE PATHS ACROSS THE CHILDS,
this approach gives the wrong answer->https://codeforces.com/contest/1101/submission/48359404
on 8th test case i have considered some big path which i should not have done. please help in this, code is quite clean.
Help T^T I still don't understand the first example provided in D. Shouldn't the output be 3 instead of 1, since the first and the third vertex has gcd greater than one with distance three? Can someone please kindly explain to me...
The path from 1 to 3 Doesn't have Gcd>1.
No.. Sorry, I still don't get it. The tree should look like: 2--3--4 2 and 4 have gcd = 2 > 1 and dist(2, 4) = 3.
I don't understand why the output is 1... By definition, dist(x, x) = 1, which means the output could only be one when there is only one node in the tree and the node is greater than one.
Can you give further explanations? Thank you very much.
You have to take Gcd of all the numbers lying in the path from u to v in the tree(including u&v).In the tree the path from node1 to node3 goes like 1->2->3,so the gcd will be gcd(2,3,4) that is 1.
Can anyone Explain the approach of problem G?
Cannot understand G :(
Could someone please explain (or point to a tutorial/explanation) why this method indeed gives us the basis vectors ? Intuitively it looks like it's doing Gauss elimination but I am having a difficult time understanding how.
base[i]saves some bit vector where the first 1 is in positioni(by first position, I mean the largest position). Now, when we want to add some bit vectorv, we try to see if we can consturctvusing the unfinished basis we currently have (that is the first loop). Why the loop works? Because, that loop tries to eliminate every bit individually (based on the property from above). If it succeeds, thenvwill have zero value. The second part. Well, ifvis not zero, then that means that our basis doesn't have a value forbase[j], wherejis the largest index, such thatv[j] == 1. And we will just add it to our unfinished basis.Here is the code I use for F2 space Gauss. It is shorter and maybe more clear.
can anyone debug the code of d given bellow?why does it give one less than actual ans?or,give me any hint
include <bits/stdc++.h>
define LL long long
define int64_t int
using namespace std;
define ff first
define ss second
define mp make_pair
define pb push_back
define ub upper_bound
define lb lower_bound
define inff 1e9+5
define M %(998244353)
//priority_queue<int, std::vector, std::greater > my_min_heap;
define FastIO ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//#define int64_t int
define lop(ii,n) for(int64_t ii = 1; ii <= n; ++ ii)
define loop(ii,n) for(int64_t ii = 0; ii < n; ++ ii)
define aloop(ii,n) for(int64_t ii = n-1; ii >=0; ii--)
define alop(ii,n) for(int64_t ii = n; ii >0; ii--)
define fox vox
string s2; map<int64_t,int64_t>mp1; int64_t vr[500006]={0}; vectorvn[200005+1];
int64_t arr[200005+1]={0},an=0; vector<pair<int64_t,int64_t> >pr; int64_t dfs(int64_t s,int64_t prm) { vr[s]=1; int64_t temp=0,tm1=0,tm2=0; loop(i,vn[s].size())if(vr[vn[s][i]]==0&&arr[vn[s][i]]%prm==0) {
int64_t t2=dfs(vn[s][i],prm); if(temp==0) tm1=max(tm1,t2); else { if(tm1<t2){tm2=tm1;tm1=t2;} else tm2=t2; } temp=1; } an=max(an,tm1+tm2+1); return tm1+1;} int64_t prr[200009]={0}; int main() { FastIO int64_t r=0,ans=0,n=1,fu=0; cin>>n;
//set<int64_t>st; //int64_t prr[n+1]; memset(prr,0,sizeof (prr)); lop(i,n){ cin>>arr[i]; r=max(r,arr[i]); fu=arr[i]; //c1=0; for(int64_t j=2;j*j<=arr[i];j++) if(arr[i]%j==0) { //if(c1<j)pr.pb(j),c1=j; prr[j]++; //if(st.find(j)==st.end()) //st.insert(j),pr.pb(j); while(arr[i]%j==0)arr[i]/=j; } if(arr[i]>1)prr[arr[i]]++;//&&st.find(arr[i])==st.end())pr.pb(arr[i]),st.insert(arr[i]); arr[i]=fu; } for(int64_t i=2;i<=r;i++)if(prr[i]>0)pr.pb(mp(prr[i],i)); sort(pr.rbegin(),pr.rend()); loop(i,n-1) { int64_t u,v; cin>>u>>v; vn[u].pb(v); vn[v].pb(u); } /*if(n==200000) { loop(i,pr.size())if(pr[pr.size()-i-1].ff>6)cout<<pr[pr.size()-1-i].ff<<" "<<pr[pr.size()-1-i].ss<<endl; }*/ for(int64_t i=0;i<pr.size()&&pr[i].ff>an;i++) { int64_t nm=pr[i].ss; lop(k,n){if(vr[k]==0&&arr[k]%nm==0){int64_t yy=dfs(k,nm);pr[i].ff-=yy;} if(pr[i].ff<=an)break; } memset(vr,0,sizeof (vr)); } cout<<an;}
Sorry,ignore the comment.
What does even and odd number of pr[x] means in G? Can someone explain 2nd para in more approachable way?
I think the following is what it claims:
Given any division D, you can always construct the xor result of some subset of {pr[x] | x is a right boundary in D} by picking some segments in D, if the subset size is even.
Then it claims this construction also works in odd case, by doing some minor changes.
e.g. Given an array A and a division A[0...3), A[3...4), A[4...5), A[5...8), A[8...11) You can construct xor result of any subset of {pr[3], pr[4], pr[5], pr[8], pr[11]}.
The proof is not hard actually, just write them down like this and you will probably see why and how it is proven: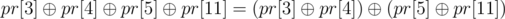
(Question C)Can anyone tell me why I am getting WA. http://codeforces.com/contest/1101/submission/48462932
You are sorting the ranges and you must give the answer in the same order as the input, so you need to store the initial position of each range. For example: 1 3 5 8 1 4 7 10. The correct output is: 2 1 2, or 1 2 1. But your code's output is 1 2 2.
What about this input in problem C ?
Should'nt this have any answer ?
For G, I forgot to find basis of prefix instead calculated basis of all the a_i's and it still passes. code how to explain this?
Because each a_i is also a linear combination of elements in prefix xor.
May you explain why the fact that each ai is a linear combination of elements in prefix xor implies that array a has a maximal basis size equal to that of prefix xor array?
Let A denotes set of ai for all i, and S denotes set of all prefix sums.
Any set of vectors which generates S (or more precisely generates span(S)) will also generate A, which gives dimension (size of basis) of S ≥ dimension of A. (If not, we have a generator of A smaller than its basis, which gives a contradiction because we can find linearly dependent vectors in any basis of A.)
On the other hand, any set of vectors which generates A will generate S, thus dimension of S ≤ dimension of A.
Maybe I am wrong because I am not a math major student, please feel free to correct me.
Thanks a lot for your reply.
But I have a concern here. If any basis b of S can generate A and has a size s < size of basis of A, why will this cause any basis of A to have linearly dependent vectors? b contains elements from S (not from A), what guarantees that we can choose a subset from A which generates A and has a size s?
To make it clear, the term "basis" used in the above refer to "A set of linearly independent vectors which generates the whole vector space". It turns out that all the bases of a space (for example, span(A)) MUST have the same size.
Consider a basis U = {u1, u2, u3, ..., un} of S with size n, and assume there exist a basis V = {v1, v2, v3, ..., vk} of A with size k, where k > n. Since A is linear combination of S, we can conclude that U is also a basis of A. It follows that all the vectors in V can be written as linear combination of elements in U. Pick the first n element of V, we can write them like this:
E1: c11 * u1 + c12 * u2 + ... + c1n * un = v1 E2: c21 * u1 + c22 * u2 + ... + c2n * un = v2
...
En: cn1 * u1 + cn2 * u2 + ... + cnn * un = vn
Left hand side of these equations are linearly independent vectors, and so does right hand side, so any linear combination of these equations must be non-zero (except all the coefficient are zeros). We can solve these equations and find a unique way to write ui as linear combination of vi, (for example, doing gaussian elimination, both side of any of the equations will always be non-zero during the process, there must be only one solution), which implies that v1, v2, ..., vn is a basis, and vn + 1, vn + 2, ..., vk, already known as linear combinations of ui, are actually linear combinations of v1, v2, ..., vn, which contradict to our assumption that all vi are linearly independent.
For the second problem, it is always possible to start from any element in A to obtain a basis. Let size of basis be k, if we have a set of linearly independent vectors V with size < k, there must exist some element x in A which is not in span(V), otherwise V is a smaller basis, a contradiction. So we just add x to V and repeat the argument until size of V is k.
This is also why all possible choices of divisions contains pr[n], but we can always construct set of linearly independent vectors contains pr[n] with size equals to the dimension, if pr[n] itself is non-zero.
By the way, since subset XOR is basically all possible linear combination of that set over field F2, it is not necessary to force U contains only element from S, it can contain any element from span(S), and so does V.
For more detail and theorem, you can refer to this.
I am very sorry for the very late reply. Thanks a lot for your effort and for the link you provided, it helped me a lot.
mohamedeltair
FoodSheep Can you explain this part? Now you just want find the division that produces the maximum number of linearly independent numbers (binary vectors). That is — the size of the basis of the space of chosen numbers (binary vectors).
A valid division is some choice of partitioning the numbers to k partitions (k>0), such that the xor-sum of any non-empty combination of partitions is non-zero. This means that if you view the xor-sum xs of each partition as a vector of bits of the binary representation of xs, all the vectors must be linearly independent under mod 2 (no linear combination of them other than the trivial combination is equal to zero).
As the basis of a set of numbers sn is a subset of sn of maximum size such that this subset's elements are linearly independent, the problem reduces to finding the size of the basis of prefix xor elements.
mohamedeltair
Thanks I got that part. But I have 1 more doubt, suppose we get our basis and it has 5 vectors, now how can we say that each of those 5 linear independent vectors correspond to xor sum of each of the segment of a division with 5 segments? That is how are we relating vectors in the basis and the xor sum of segments in the division.
vivace_jr
If we have k segments, where the left and right indices of the ith segment are l(i) and r(i), and pref is our prefix-XOR array, the XOR-sum of the ith segment will be pref[r(i)] XOR pref[l(i)-1] (assuming 1-based indexing).
Note that for all l(i)>1, l(i)-1 = r(i-1), and for l(i)=1, l(i)-1 = 0 (has no significance when XORed with anything). This implies that any combination of segments will have an XOR-sum consisting of pref[r(i)] elements.
Also any combination of pref[r(i)] elements will have an XOR-sum equal to the XOR-sum of some combination of segments (to include some r(i), either include the ith or the (i+1)th segment (exactly one of them), and to not include some r(i), include both the ith and the (i+1)th segments or don’t include any of them).
Therefore, all combinations of segments and all combinations of pref[r(i)] elements will result in the same XOR-sums.
My kotlin solution for E keeps timing out. The tutorial says to choose your IO functions carefully. Is there a better option than readLine()?
use printf and scanf
Problem D can also be done with the help of Centroid Decomposition.
Very similar to the problem PRIMEDST
Just a small change is required. Figure it out yourself. It's fun. :)
Consider this solution for reference : LINK
What are the prerequisites of problem G? This paragraph:
"This way we can collect all subsets of pr[x] for some division. Now you just want find the division that produces the maximum number of linearly independent numbers (binary vectors). That is — the size of the basis of the space of chosen numbers (binary vectors)."
has a great jump over details which need more explanation.
After some searching found this which may be helpful:
Efficient algorithm to find whether a subset of an integer array exists,the xor of all its elements is a given value?
Can anyone please confirm the complexity of PikMike's solution for question D:Gcd Counting. As I think its factorization would take n*sqrt(A) time.
In case somebody didn't understand tutorial of problem G, here you can find a blog explaining the whole idea of gaussian elimination behind.
Isn't G an easy version of ABC 223 — H — XOR QUERY?
i am solved the problem D. using rerooted technique.
here is my solution to D in O(NlogMAXN) if someone is interested https://codeforces.com/contest/1101/submission/174363913
I get that for problem G, the maximum possible number of segments in a division is the size of the basis. However, how to prove that such division exists? Would it be possible to reconstruct an actual valid solution?