I couldn't seem to find a blog entry for this contest (COCI Round 4), so I created one! Let's discuss the problems of the fourth round of the COCI since the contest is already over. (http://hsin.hr/coci/)
Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/21/2024 14:23:37 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How did you guys solve the last problem, Akvizna?
I am the author of the last problem.
Let dp[i][j] be the maximum possible amount that Mirko can win in game with i rounds and j opponents at the beginning, divided by 100 000. dp[i][j] = min (dp[i — 1][j — k] + k / j), for k in 1, 2...j It is enugh to get 20 points.
To get 50% you need some observations. Let a_1, a_2...a_k be the number of people that have been thrown out in each round. It's not hard to prove that a_1 >= a_2 >= ... >= a_k. Also a_1+a_2+...+a_k = n so we get a_i <= n/i, because otherwise we would have a_1+a2+...+a_k > n. Because of that dp[i][j] = min (dp[i — 1][j — k] + k / j), for k in 1, 2,...n/i so total complexity is now n*(n+n/2+...+n/k) = n^2*(1+1/2+...+1/k) = n^2 log k and that is enough to get 65 points.
To get 100% you have that see that dp[i][j+1] — dp[i][j] <= dp[i][j] — dp[i][j — 1] which means that we can use aliens trick.
More about aliens trick you can learn here. https://ioinformatics.org/files/ioi2016solutions.pdf (the last problem, subtask 6.)
Wow, never before had I heard of Alien's trick, thank you so much! By the way, really nice problem, especially (now that I know how to solve it) the second subtask.
Thanks!
You can eliminate the log factor. dp[i][j] = min(j × dp[i - 1][k] - k) / j + 1, so it's a classical problem of finding a minimum y-intercept of function dp[i - 1][k] × x - k, aka convex hull trick.
If you are not very confident on the precision, then you may prefer faster routines to make long doubles work..
Yes, and you can also use divide and conquer optimization (quadrangle inequality).
I need to know how to solve the third problem kisik, still don't know why my code fails so bad haha
Nevermind, didn't read the FAQ. It says:
4. Should I use %lld or %I64d for long long input/output in C++?
%lld.
Yeah I've just read it :(
I'm not sure if you still need it, but I'll leave you my code for the problem here Code
I did something like that, mine only works for N <= 1000. I will check my code for correctness. Thank you!!
How to solve Slagalica?
Suppose after a mega move number at node X moves to node Y. Add an edge between X and Y. If you do this for all N * M nodes, the whole parallelogram will be decomposed into some simple cycles. K must be equal to lcm of those cycle lengths.
Let the prime factorization of K be p1a1p2a2...pkak. We must have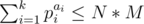 . This condition is both necessary and sufficient for the existence of answer. Because it is possible to swap any 2 adjacent nodes of the parallelogram with the given operations. For example applying T(x - 1, y - 1), T(x - 1, y - 1), R(x - 1, y - 1) consecutively swaps numbers at nodes (x, y) and (x - 1, y). Since now we can swap 2 adjecent numbers, it's not hard to construct cycles of lengths p1a1, p2a2, ..., pkak
. This condition is both necessary and sufficient for the existence of answer. Because it is possible to swap any 2 adjacent nodes of the parallelogram with the given operations. For example applying T(x - 1, y - 1), T(x - 1, y - 1), R(x - 1, y - 1) consecutively swaps numbers at nodes (x, y) and (x - 1, y). Since now we can swap 2 adjecent numbers, it's not hard to construct cycles of lengths p1a1, p2a2, ..., pkak