Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
vector<int>a({l1, r1, l2, r2});
int ans1 = 0, ans2 = 0;
for (auto it : a) for (auto jt : a) {
if (l1 <= it && it <= r1 && l2 <= jt && jt <= r2 && it != jt) {
ans1 = it;
ans2 = jt;
}
}
cout << ans1 << " " << ans2 << endl;
}
return 0;
}
1108B - Divisors of Two Integers
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
cin >> n;
multiset<int> a;
for (int i = 0; i < n; ++i) {
int x;
cin >> x;
a.insert(x);
}
int x = *prev(a.end());
for (int i = 1; i <= x; ++i) {
if (x % i == 0) {
a.erase(a.find(i));
}
}
cout << x << " " << *prev(a.end()) << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
string s;
cin >> n >> s;
vector<int> p(3);
iota(p.begin(), p.end(), 0);
string colors = "RGB";
string res = "";
int ans = 1e9;
do {
string t;
int cnt = 0;
for (int i = 0; i < n; ++i) {
t += colors[p[i % 3]];
cnt += t[i] != s[i];
}
if (ans > cnt) {
ans = cnt;
res = t;
}
} while (next_permutation(p.begin(), p.end()));
cout << ans << endl << res << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
string s;
cin >> n >> s;
int ans = 0;
for (int i = 0; i < n; ++i) {
int j = i;
while (j < n && s[i] == s[j]) {
++j;
}
string q = "RGB";
q.erase(q.find(s[i]), 1);
if (j < n) q.erase(q.find(s[j]), 1);
for (int k = i + 1; k < j; k += 2) {
++ans;
s[k] = q[0];
}
i = j - 1;
}
cout << ans << endl << s << endl;
return 0;
}
1108E1 - Array and Segments (Easy version)
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(NULL));
const int INF = 1e9;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, m;
cin >> n >> m;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
vector<pair<int, int>> b(m);
for (int i = 0; i < m; ++i) {
cin >> b[i].first >> b[i].second;
--b[i].first;
--b[i].second;
}
int ans = *max_element(a.begin(), a.end()) - *min_element(a.begin(), a.end());
vector<int> res;
for (int i = 0; i < n; ++i) {
vector<int> add(n + 1);
vector<int> cur;
for (int j = 0; j < m; ++j) {
if (!(b[j].first <= i && i <= b[j].second)) {
cur.push_back(j);
for (int k = b[j].first; k <= b[j].second; ++k) {
--add[k];
}
}
}
int mn = INF, mx = -INF;
for (int j = 0; j < n; ++j) {
mn = min(mn, a[j] + add[j]);
mx = max(mx, a[j] + add[j]);
}
if (ans < mx - mn) {
ans = mx - mn;
res = cur;
}
}
cout << ans << endl << res.size() << endl;
shuffle(res.begin(), res.end(), rnd);
for (auto it : res) cout << it + 1 << " ";
cout << endl;
return 0;
}
1108E2 - Array and Segments (Hard version)
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(time(NULL));
const int INF = 1e9;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, m;
cin >> n >> m;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
vector<pair<int, int>> b(m);
vector<vector<int>> lf(n), rg(n);
for (int i = 0; i < m; ++i) {
cin >> b[i].first >> b[i].second;
--b[i].first;
--b[i].second;
lf[b[i].second].push_back(b[i].first);
rg[b[i].first].push_back(b[i].second);
}
vector<int> ansv(n, -INF);
vector<int> add(n + 1 , 0);
int mn = a[0];
for (int i = 0; i < n; ++i) {
ansv[i] = max(ansv[i], a[i] - mn);
for (auto l : lf[i]) {
for (int j = l; j <= i; ++j) {
--add[j];
mn = min(mn, a[j] + add[j]);
}
}
mn = min(mn, a[i] + add[i]);
}
add = vector<int>(n + 1, 0);
mn = a[n - 1];
for (int i = n - 1; i >= 0; --i) {
ansv[i] = max(ansv[i], a[i] - mn);
for (auto r : rg[i]) {
for (int j = i; j <= r; ++j) {
--add[j];
mn = min(mn, a[j] + add[j]);
}
}
mn = min(mn, a[i] + add[i]);
}
int ans = *max_element(ansv.begin(), ansv.end());
vector<int> res;
for (int i = 0; i < n; ++i) {
if (ansv[i] == ans) {
for (int j = 0; j < m; ++j) {
if (!(b[j].first <= i && i <= b[j].second)) {
res.push_back(j);
}
}
break;
}
}
cout << ans << endl << res.size() << endl;
shuffle(res.begin(), res.end(), rnd);
for (auto it : res) cout << it + 1 << " ";
cout << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
vector<int> p, rk;
int getp(int v) {
if (v == p[v]) return v;
return p[v] = getp(p[v]);
}
bool merge(int v, int u) {
u = getp(u);
v = getp(v);
if (u == v) return false;
if (rk[u] < rk[v]) swap(u, v);
rk[u] += rk[v];
p[v] = u;
return true;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
ios_base::sync_with_stdio(0);
int n, m;
cin >> n >> m;
p = vector<int>(n);
iota(p.begin(), p.end(), 0);
rk = vector<int>(n, 1);
vector<pair<pair<int, int>, int>> e(m);
for (int i = 0; i < m; ++i) {
cin >> e[i].x.x >> e[i].x.y >> e[i].y;
--e[i].x.x;
--e[i].x.y;
}
sort(e.begin(), e.end(), [](pair<pair<int, int>, int> a, pair<pair<int, int>, int> b) {
return a.y < b.y;
});
int ans = 0;
for (int i = 0; i < m; ++i) {
int j = i;
while (j < m && e[i].y == e[j].y) {
++j;
}
int cnt = j - i;
for (int k = i; k < j; ++k) {
if (getp(e[k].x.x) == getp(e[k].x.y)) {
--cnt;
}
}
for (int k = i; k < j; ++k) {
cnt -= merge(e[k].x.x, e[k].x.y);
}
ans += cnt;
i = j - 1;
}
cout << ans << endl;
return 0;
}











I know that there are some troubles with the editorial. It will be available after fixing these issues. Please, wait a bit :)
lol
@Vovuh In (question E1) after reading the editorial what i understand basically you just assume that every i is maximum value in array and you run a loop through all segments if this segment include i then discard otherwise run a loop. right???
Yes, it is true. Because we don't know which element will be the best, we iterate over all possible candidates. And then we apply only segments which can be useful for us.
But in the implementation you are working with i or decreasing value in the segments which covers i. But you said i is the assumed maximum value. Please clear this. Thanks. (>>>>update( understood ) >>> i didn’t see the whole bracket in the condition and making false.
Additional question. Why shuffling?
What's the O(mlog(n)) approach in E2?
With lazy segment trees you can subtract/add 1 to A[l:r] in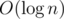 time and find max/min of A in O(1), allowing for a
time and find max/min of A in O(1), allowing for a 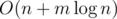 solution.
solution.
Wooooooow!
Very clever solution. Actually the main idea is working with intervals in a clever way (applying intervals on an index of array and reversing the effect of previous applied intervals), not using segment tree. Do you agree or I misunderstood something? :D
Yeah exactly, the segment trees are only there to speed things up.
How someone should get to this solution? Have you solved a problem with similar idea before?
It's always difficult to say how one comes up with a solution.
Generally, I just have a ton of different implementations of segment trees so I just pick whatever I need, so for me this problem was just about how to solve the problem using operations I can speed up using segment trees. I'm a big fan of segment trees and use them in most competitions, like I even implement my own heaps using segment trees.
For this specific problem I think that a nice way of thinking of it is that you want to try maximizing max(A)-A[i] for each i. The easy way to do this is to subtract 1 from all intervals that contain i, which is an operation that easily can be done with segment trees.
Can u share in detail your intuition behind the proof of optimality for problem E? I couldn't come up with any proof during contest :( It would be great help:)
Proof: First, note that we are only DECREASING elements. Next, choose each element to be the maximum. This part is brutish, so it doesn't need any explaination hopefully. We are not doing anything tricky here. Now, If we were to apply a segment which contains the current assumed max, its always bad. Why? suppose we applied this operation because we wanted to lower a value in that same segment. But guess what? everything gets decreased by the SAME amount, so the relative difference remains the same. What more, if the optimal minimum lied outside, our gap is minimized further, as we are decreasing the max. Also, we should apply all segments which do not contain my current max, because, we are already assuming that our maximum wont come from there. However, our minimum might. So we might just decrease everything.
Can you please explain how the complexity turns out to be O(n+mlogn) ? What I was thinking that for each of the element in the array we have to find the segments in which they fall and use lazy propagation to update them. So doesnt that turns out to be O(nm + mlogn) ?@pajenegod
There is a trick to get it down to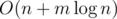 that I use in my solution as mentioned by mohammad74. The idea that once you added all the segments that contain i then you can easily do it for i + 1, you just have to add the segments with l = i + 1 and remove those with r = i. This trick makes it so you only have to add/remove each segment once.
that I use in my solution as mentioned by mohammad74. The idea that once you added all the segments that contain i then you can easily do it for i + 1, you just have to add the segments with l = i + 1 and remove those with r = i. This trick makes it so you only have to add/remove each segment once.
Can pajenegod please look at my solution? I couldn't figure out why I am getting error at the 7th test case. I am following the same approach as your solution.
To be honest your code is a bit messy and the way you use global variables doesn't make it easier to understand, so its difficult for me to say exactly what is wrong.
However just reading the code there is one thing that I strongly suspect is wrong. It looks like you use the same kind of segment tree that I'm familiar with, but in that case your n has to be a power of two. Are you sure your segment tree code is working?
You can see how I get around this with the segment tree in my solution. In the constructor of the tree I calculate the size m which is n increased to be a power of 2. Pretty sure you have to do something similar.
pajenegod
First, the algorithm for segment given in this blog works for any arbitrary array size as you can see it is clearly mentioned in the Arbitrary sized array section. I verified it through my code as well.
Second, The error in my code was in inc(l,r,value) function. I was calling build(l) and build(r-1) instead of build(l+n) and build(r+n-1).
Third, Thank you for directing me towards amazing blog about segment tree.
Here is my final submission. I tried to make it less messy :).
Can someone explain the how to solve F using binary lifting?
For each edge not include in MST you need to check if this edge can be included without increasing the cost. Suppose the edge is from u to v with weight w.if we connect this edge in our mst, then a cycle would be formed. To get back to minimum cost for MST ,we can delete the edge with maximum weight, the question now is there any edge in path from u to v which has weight equal to w(There can't be any edge with weight greater than w in this path).
Binary Lifting would be used to find the maximum weight in path between u to v.When you compute LCA, anc[i][j]->represents (2^j)th parent of i, you can also store maximum edge apppearing on path from i to its (2^j)th ancestor.Querying is similar to LCA Querying.
You can understand this easily from my code. My submission
Got it. Thanks A lot!
What I understood is that after building MST, we check for every edge which is not the part of MST (say between u and v with weight w) that if there exist a edge in MST on the path between u and v with weight w then we will increase ans by one.
Please correct me if I am wrong?
Yeah that's correct.
i have a doubt ... is it true that if we take any MST in a graph the maximum weight edge in the path of 2 node a and b is same in all MST. gaurav172
For Problem E2, you can write an easy O(M^2) solution. Since we only care about the segments given in the input and minimum and maximum value, we can cut the given array to O(M) size by taking the information of range of segment, minimum and maximum of segment and apply easy approach given in the editorial
but it should be O(n) since you have to read the array of size n
Yes, just like in editorial of E2, solution suggested is O(m log(n)) which is after reading array. Similarily in my solution, after reading array and converting it to new array of size O(M) it's complexity is O(M^2).
can you link your solution here . your solution may help to understand easily
I understood from this solution link
Thanks vovuh :)
Under pressure, only solution that felt safe for question D is DP.
Could you explain me, how to solve D using DP ?
Thinks of it as calculating the cost of making the ith letter with R.
When i = 0, then cost = 1 if s[0] != R and cost = 0 if s[0] == R
For any ith index
cost[i][R] = min( cost[i-1][B], cost[i-1][G] )+1, if s[i] != R
cost[i][R] = min( cost[i-1][B], cost[i-1][G] ), if s[i] == R
Similarly u can extend for it for other colors...
For building the solution back u need an another array to keep index of min value u r getting from ... a approach similar to LCS...
See code for more reference
haha same for me man
DELETED
can anyone help , what is wrong with this O(n^3) solution of B? https://codeforces.com/contest/1108/submission/48890311
Check this U just need to add one more condition, the situation when d[k] == xx or d[k] == yy and at the same time it divide the other one then it to be the answer the frequency of d[k] should be two.
Thank you so much ^_^ . I understood my mistake now. if frequency of element is 1 then it should not be able to divide both x and y but only one of them. Thanks again.
Can someone please explain how to solve E1 using segment tree???
U can solve this even without segment tree Code Link
With segment tree Code Link
U can easily extend this solution for E2 by adding lazy propagation Your text to link here...
For reading reference u can check Segment Tree
48969069 Can you help me on this ? Why even after lazy propagation it is giving TLE ?
U just need a little modification for updating the query.
For example let the three queries are like (1, 2), (2, 4), (1, 6), (3, 5) Firstly we will update all the query (-1) in the segment tree. Then for processing the first element we know the queries 1 and 3 should be undone. Then we move to the second element, here we know only the query 2 should be undone ( since 1 and 3 are already undone ). Then we move to third element, here the 1st query should be updated (-1) as we have undone it and query 4 should be undone.
In short first execute every element. Than for every ith element we update the query which have finished at i-1th index and undone the query(+1) starting at ith index. Submission
Thanks a lot!! And I am extremely sorry by mistake your comment has been down voted by me and it's not even returning back to same.
Thanks for help
what is the complexity of E2 with segment tree. i cant figure out it
I think it is O(n+m*log(n))
May be 0( nm+ mlogn)
Yup you are right ... it is O(nm + mlog(n))
if you could describe your approach for E2 anyone can understand easily. already wasted 4 hour waching your code, but cant figure out what exactly happened to it
Check out this.
atlasworld Let us say the ai be the final minimum value. The ai will only be minimum if we apply all the queries that cover the ai element. After performing the queries we take out the maximum value of the resulting array using the segment tree. We follow the same procedure for all the elements.
Hi @Vovuh,
For problem F, the first approach. Because we need to find the minimum ops, How to prove that, any of the different MST result to same number of ops?
Suppose you build an MST. For each edge that does not belong to your MST, you must find out a smallest-weight spanning tree that must contains the edge. Let call it the second MST of that edge. Basically the approach mentioned in the tutorial is a way to find a second MST of an edge.
Well from here we can deduce that we must increase all the "bad" edges, which are the edges that:
Any number of ops lower than number of "bad" edges in the original graph would cause your MST not unique, because if a "bad" edges exists, you could construct another MST that different from your MST (because two spanning trees differ in that "bad" edges, your MST does not contains it while the new MST does) and both MST have equal weight.
Thanks. Well, I think I will understand you after I figure out the second MST algorithm.
Every group of k-weight edges, we will keep connecting them until we cannot connect anymore.
Therefore, subsequent options of "good" k-weight edges will be the same, no matter what mst we build.
Since both our good edges and the amount of edges we used (n-1) are the same, our answer will be the same no matter what mst we build.
that make sense
Thanks for your effort :) Waiting for your next Div.3 Contest
Can someone please explain why does this solution give TLE verdict for Problem 1108E2 — Array and Segments (Hard version): Solution Link
Trick on performing queries : Let we have 10 elements in total and queries are of the form (1,4), (3, 6), (2, 8), (4, 6), (1, 10). So by pre-processing we can calculate the queries which are affecting the ai element, { {1, 5}, {1, 3, 5}, {1, 2, 3, 5}, {1, 2, 3, 4, 5}, ... } . To perform these queries we can either follow the naive approach i.e. while processing the 1st element we perform queries 1 and 5, then extract the max, update the result and undo the queries 1 and 5, then again move to 2nd element perform 1, 3 and 5 queries and get max and undo them. But we know that the queries performed for 1st element is also needed for 2nd elements, hence we will change the preprocessing a little bit , instead of storing the queries affecting the ith element, we will store queries that are starting with ith element and queries that are ending at (i-1)th element.
Submission
wow! , your solution is very interesting thanks <3 !!!
Then let's apply all segments with right endpoints equals to the current position straight-forward and update the value mn with each new value of covered elements. Just iterate over all positions j of each segment ends in the current position, make addj:=addj−1 and set mn:=min(mn,aj+addj).
In the editorial of problem E2, Why are we doing this portion? vovuh
We apply all segments naively because we are needed to update the minimum value on the prefix of the array but we want to do it without any data structures. And this method works fine for the given constraints so we do it so.
Thanks for solving problems E2 and F!
1108A
I guess there's a bit easier solution: we can assume that the numbers we need (A and B) are L1 and R1, respectively. And if they are equal, change B to R2.
Problem D easily can be solved by iterate over the s the input string if(s[i] == s[i-1) change s[i] to letter not equal to s[i] && not equal to s[i+1] you have three different chars R, G, B so there is always a letter that you can use with minimum cost
Yes that is also my solution.
It is just under your comment
Actually, Problem D has a better solution.
When a garland is not diverse, it will have some pairs which are the same,like
GG.Thus, we can iterate over the string. If we find a pair that is not diverse, we can change it to
The second color, if the next one is still the same,or
The third color, if the next one is not the same.
For example, given a string
BBBGGGRGBRun this algorithm on it, we get:
BGBGGGRGB
BGBGBGRGB
It is indeed the solution.
In Question C, I am using C++ 11 . when i am using '+' for concatenation of string, it fails with TLE, but when i use string::push_back() , it gets AC. The rest of the code is same. Why does it happen? I thought string concatenation in c++ using '+' should take linear time. Can someone please help.
TLE with '+' Submission
AC with push_back() Submission
It seems that string::push_back is faster than '+'.
Ideally it shouldn't be as in the following stackoverflow articles, some people have mentioned that '+' operator overloading fun in c++ uses push_back() internally. Also it said that C++ string is mutable and should not create new string every time for each character concatenation.
string-concatenation-complexity-c++
Append a char in c++
So, not sure why this happened.
Im not sure but things Ive know about string that its a container template, just like a vector, and if you use string=string+char, maybe it will take O(1) to do this like a push_back wt vector, but when you use string1=string2+char or string=char+string (push front), in this case, it will take you O(n) to complete, also like a vector when we try to make a function to push front, no way to do it in less than O(n). Hope these make sense to u ;)
Yes, you are correct. Here i was only doing string = string + char So, it should have taken O(1).
yep, Ive just looked at ur code wt tle, and I saw that u use +, but in the way that it took O(n) to do. If youve ever studied about OOP in c++, you will have a note that when a object do a operator (like +), it will copy the result to a temp var, and then it will take a step to do operator = to copy this temp var to the real result var. You can get ac by changing string=string+char to string+=char (or string.push_bach(char)). Im sure that u get ac wt this code. Happy coding!
Oh yes, completely forgot that "=" operator is also overloaded and it will come into play after '+' overloading fun is called, and might copy the whole string from rhs to lhs.
"+=" operator worked, so in "+=" operator overloading fun for string, it must be doing like push_back() and hence O(1)
Cool. Thanks a lot.
I have a different solution for E2, which might be a bit easier to get. However, its still O(n*m) For each presumed maximum: (this step is O(N)) We basically divide the segments into two halves as mentioned and then do the following: We process the openings and endings as 'events'.The minimum basically lies between two events. Now , if we knew the minimums between each 2 consecutive events, we could compute the answer in O(M) time. This is because there are atmost O(M) events and so O(M) inbetween regions. Also, for each region, we know the amount we have to subtract from the minimum of that region. I call these "reduced minimas". Now if we just compared these "reduced minimas" and took their minimum, that would be my global minimum. Only thing left is how two find the minimum value in a range of the original array without traversing the entire region? Well, use sparse tables, as they support O(1) range min/max queries.
O(1) in sparse table RMQ
huh, spent half a day trying to implement (segment, segment) (+, max) tree, with no luck (did not use any references), then found out passes easily using sqrt decomposition...
passes easily using sqrt decomposition...
Edit: I guess good enough is sometimes better than optimal.
Edit2: more precisely
lol : ) , what u did for G ?
Don't understand the question, could you clarily please?
how u solved g? i am not able to figure out what the ques. is saying.
I don't see problem G, do you mean F?
Edit: in the post I was speaking of problem E2
yes , f ! what problem is saying . how ans . in example 2 is 0
For F I just did classical Kruskal algorithm, but before adding any edge I check how many other edges with the same cost can I add, substract the actual amount of edges added (of certain cost). Seemed plausible, it might have been a heuristic, but turned out accepted, so it is probalby correct.
It's sad that I made up a solution to problem E with O(n log n + m log m + nm) time complexity got TLE.
I know that the intended solution is more efficient, but it's so sad that I can't pass it.
btw, can someone help me optimize it?
I've got a different solution for E2, which can be done in O(n+m^3) or O(n+m^2) and get an AC. First, imagine the array is "cut into pieces" by the ls and rs of the segments. (e.g. if n=10, m = 3, and the segments are [1, 5], [2, 9], [3, 7], then the whole array will be cut into [1], [2], [3, 4, 5], [6, 7], [8, 9], [10]). Since there are m segments, the array will be cut into at most 2m+1 pieces. Within each piece, only the maximum and the minimum of that piece are possible to contribute to the answer (become the real max/min of the whole array after operations). Hence, we reduce the problem to n<=2m+1. Then, we can simply use the solution for the easy version to achieve O(n+m^3) or O(n+m^2)
Please explain the approach of how to consider each segment as there can be total $$$2^{m}$$$ variations possible in problem E2.
Can someone please explain Segment tree approach in E2 problem. I tried Lazy Propogation (got AC on E1, but TLE 13th TC on E2). For every element assumed to be resulting array, max element, I found the answer by updating the segment tree with all the non-intersecting segments with adding '-1'. Then restored these segments by adding '+1', so as to compute ans for the next element. My submission link: https://codeforces.com/contest/1108/submission/68416008
hilarious DSU solution i wrote for D. Diverse Garland because i was bored https://codeforces.com/contest/1108/submission/138819168
i am very glad to solved the problem F, and this problem is very very good . because if you would like to solve this problem, you must have to be deep knowledge of Kruskal algorithm. the question is how the Kruskal algorithm works?. you should visualizing that.
Alternate O(n*m*log(m)) solution to E2 using a sparse table and modified scanline algorithm.
https://codeforces.com/contest/1108/submission/195282126