In this problem you should count number of consecutive pairs of equal letters. It can be done using one cycle and O(N) time.
In this you should realize the given process. You should t times swap elements i and i + 1 if on the place i was a girl and on the place i + 1 was a boy. You should not push some girl to the left multiple times at once. The solution can be written using O(N·T) time.
This problem can be solved using constructive algorithm. We will use inductive approach. At first, we have matrix of size n and n - 1 ones in it. Therefore, there is a column with no ones in it. So, we put this column to n-th place. In this case, the lower right element will be 0. Then find any row with at least one integer one and put it to the n-th place.
After these operations the element in cell (n, n) equals to 0 and the last row has at least one integer one. Therefore, we can reduce the dimension of our problem, that is n: = n - 1. In our new problem we have no more than n - 2 ones. So, we can solve this problem using the same algorithm. When n equals to 1 you should finish algorithm, because there is no ones left. This algorithm uses O(N) swap operations, no more than two for every n.
I'll tell a few ideas how to solve this problem. Firstly, describe the solution with time O(N4). Consider every edge (u, v) of length len where could be the answer point. Let this point lie at a distance x from vertex u. So, the distance from this point to vertex i would be min(x + d[u][i], len–x + d[v][i]), where d[x][y] — distance between vertices x and y. Equate these values and get the critical value x for vertex i, x = (len + d[v][i]–d[u][i]) / 2. It follows that the answer to the problem is half-integer. So, for every edge and every other vertex we get set of critical points. We should check them all include the vertices of the graph (ends of the segments). This solution may probably pass with some optimizations.
Another solution with complexity O(N3·log2). Multiply all weights by 2. Consider every edge where should be the answer and make binary search for the answer (in integers). To check some current value you should consider every vertex i and assume that the answer is achieved in this vertex. In this case, the answer point must lie on this edge <= some value l[i] or >= some value r[i]. This subproblem is solved using offline algorithm using sorting events and maintaining the balance.
Also, you can use ternary search on every edge of the graph. But you should divide every edge on several segments and find the answer on every segment, because the ternary search is incorrect in this problem.
The last two solutions can provide accepted, if you realize them carefully. Also note, that there is the solution with complexity O(N3) by the author RAD.
266E - More Queries to Array...
This problem can be solved using data structure. We would use segment tree, we will support k segment trees for every power. At every vertex we will calculate weighted sum of the appropriate power, also we will save some number that indicates the color of the whole segment, if any.
User Egor in comments to the post and user mexmans in comments to the tutorial tell their formula to get the answer. I try to describe how to get them by yourself. Firstly, you should write what value your segment tree gives. The tree can calculate the sum 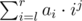 . You need to calculate the sum
. You need to calculate the sum 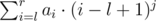 , you can write it also as
, you can write it also as 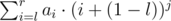 . Then you should write the last sum for some first powers (at least three) (at piece of paper) and subtract the second sum (what you need) from the first sum (what your tree can calculate). You get an expression that describes what should be subtracted to get the answer from the value what you tree can calculate. This is just the Newton binomial without the highest power.
. Then you should write the last sum for some first powers (at least three) (at piece of paper) and subtract the second sum (what you need) from the first sum (what your tree can calculate). You get an expression that describes what should be subtracted to get the answer from the value what you tree can calculate. This is just the Newton binomial without the highest power.
So, the answer for power j is expressed as the subtraction of the value of query to your segment tree and the Newton binomial, with all powers that are less than j (these values can also calculated using your segment tree). Partial sum of the powers and binomial coefficients can be precalced. The solution has the complexity O(N·K·log(N)).











tutorials for d & e?
Bit patience my friend :)
It has not been ready yet.
For D i tried the following approach but somehow couldn't finish debugging it.
Will it work ?
In problem C the important part is how can you find the 0 row fast (I mean the row with all numbers 0 in it), because you do it O(N) times and naive way (O(N^2)) is not sufficient. I used some dynamic arrays and updated them after each swap. For me the difficulty was in implementation and not in the algorithm, I got it in about 5 minutes.
n = 1000 whats the problem with n^2 algo?
you do N^2 thing O(N) times, in total it becomes O(N^3). I mean in O(N) times you will have to find 0 row in remaining square. That's not a straightforward thing to do, for me it was harder than the part that is written in the tutorial.
the two steps are independent, so this gives O(n^2), which is feasible. you just need an array of size n counting the number of ones in each column to search for the appropriate column in O(n)
that's what I did actually
D and E ? at least some hint ?
E: 1) Let's understand how to solve this problem if k for all queries to calculate the sum is equal to 0. It's quite easy to do it: we can just use a segment tree.
2) Let's learn to answer queries where k is greater than zero. Let's assume that we know a correct answer for a node's left child and right child. We need to merge node's children answers. To do it, we can figure out the following formula: answer for current node and power k ans[k] = ans_left[k] + ans_right[k] + sum for all 1 <= j <= k ans_right[k — j] * L ^ j * c[k][j], where ans_left and ans_right are the answers for node's children, c[k][j] is a binomial coefficient and L is the length of a segment represented by the left child of the node.
3) However, we still don't know how to process assign queries. But this is rather simple: if we precalculate prefix sums for all powers, we'll be able to find a value for a certain node in a tree in constant time even if its value has been updated.
Such solutuion works in O(N + M log N) time.
thanks for the hint
It seems that I had underestimated the C problem — very interesting idea to solve it.
Thanks for tutorial!
Could I solve D Problem, using Hakimi algo, for searching an absolute center of Graph?
Article in Russian is here:
http://www.uchimatchast.ru/teory/abs_center.php
(algo in the bottom of the page)
For problem C there is an O(n) solution. 2997252 (this is not my original idea, i learnt it from 2993213 and edit the swap part to make it O(n)) The main idea is that after j steps, for all 1<k<=j, kth marked cell will lies in column 1 to k, row c+1(c=its column number) to j+1.
a
You are right that two swaps are needed, but by definition of Big-O notation, there is no difference between O(N) and O(2*N). O(N) means there is some fixed constant M such that algorithm works in time M*N for each input of any size N.
a
but it doesnt mean ,your swaps take o(2*n) ......
a
Tutorial for chinese version chick here
My idea for problem D is using ford-bellman, then with every edge[i], I find the furthest way from edge[i].x, from edge[i].y without pass through the edge[i] and determine the point, but I get WA. Anyone can explain, or have a wrong test case for that ? Thank you for helping, and sorry for my poor english :).
open your submission, you'll find the test cases below your code, and you'll find the one that gives your WA.
I know about that, but that one is too big.
How do you determinate the point on edge? You can't use ternary search, because function on it isn't convex
point = ( furthest(edge[i].x) — furthest(edge[i].y) + edge[i].w )/2; Is it right ?
No, it isn't. I thought so too, but Egor said me, that function on the edge is piece-wise linear. So you must disintegrate it on the segments. I'm still thinking, how to do it
there is a Monotonicity when the answer(ans) is increasing , you will find more such points that satisfy the condition Max_shortest_distance <= ans,so i think you can try binary search of this problem .
Have you passed the solution? If yes, please write the idea :)
Still waiting for D and E solutions...
:-w
I think you also should provide the link to good code for each problem in contest with each problems explanation in tutorial. [ Best : Good and nice implementation and better complexity]
tutorials for D & E pls!
You can find editorial for D from problem C at here.
Hope someone can do some explanation on E!
thanks, nice explanation of problem D
Sorry but I don't think so: In the discussion of D we read: " It follows that the answer to the problem is half-integer. So, for every edge and every other vertex we get set of critical points. We should check them all include the vertices of the graph (ends of the segments). This solution may probably pass with some optimizations." I don't think that it is true for the 3-rd example. Even if not so, the proof is quite ambiguous.
whats that?
there are only solutions. where to read problems ?
a
Great source for learning the Min. Diameter Spanning Tree but the link seems to be broken. Here's the web archive link for the pdf: Link
Here is my approach that gets WA.. but i don't know why..
First i compute the shortest distance between pairs using floyd warshal, then iterate all pairs getting the furthest node to each one of them.. then using binary search i get the optimal place on the road of those pair.. getting the min for every pair and printing it.
Can anybody tell me whats the problem of my solution?
The tags for Div2B include Max flow. Can anyone elaborate on how to model this problem as a graph?