XIX Open Cup Grand Prix of Gomel takes place on Sunday, February 10, 2019, at 11:00 AM Petrozavodsk time.
The links to the contest:
You need an Open Cup login to participate.
The Division 1 contest also serves as the open qualifying contest for MosCode Festival 2019.
I'm the writer of all the problems. Let's discuss them here after the contest!










When I enter the link and the OpenCup login it says "The virtual contest is in progress. You are not allowed to participate". Is it the same for everybody?
Which OpenCup login do you use?
zagreb02 we used it for the first part of the sesaon without any problems.
Hm, maybe its because start time (11:00) was not set when you looked at the contest?
Probably, now everything works, thanks.
Same problem again, 15 minutes till contest!
Same problem right now?
How to solve F,B?
F: realize that vertices in L(L(G)) correspond to pairs of adjacent edges in G, and edges in L(L(G)) connect pairs that have a common edge in G.
For each edge e in G, consider pairs including e. Can you find how many connected components these pairs would be forming at the moment if we ran Kruskal's algorithm on L(L(G))? If you can, then you know the contribution of e to the result.
B: greedy. Very roughly speaking, you want team A to beat team B on penalty and, alternately, team B to beat team A on the number of problems (or vice versa). How would you achieve that?
Setting problem A, I pursued one goal... Prime New Year Contest 2019.
Good job, jqdai0815!
How to solve I. I could realise that we need to find scc's in graph where i->j if j is preferred over i. And take problems from sink onwards. How to construct them fast. Or is the idea totally different?
I don't know how to construct SCC's fast either :)
The idea is to take the last p vertices of any hamiltonian path.
Am I correct in saying that a suitable subset can be found in O(NK) using the quickselect algorithm as opposed to O(NK log N) from sorting?
I think so.
How did you write the checker for this problem?
As I remember, he precomputed the SCC in O(n2) time, and fed them to the checker :D
That's a good question :) I precalculated SCC's in O(nk2) and provided them to the checker in the answer file.
I can see how to find a hamiltonian path in nlogn, but still I can't see why that's an answer. Can you please explain?
Upd. Actually this is easy to map that top p nodes in hamiltonian path is also top p nodes in scc, but still I feel it's quite unintuitive to jump from scc to hamiltonian. May be knowing/coming up the fact that a complete directed graph has a hamiltonian path was the main key to the solution? I am wondering what was your motivation to sort / hamiltonian path?
You can "move" any subset of size p along the hamiltonian path to get to the last p vertices in a finite number of steps -- each with non-zero probability. Hence for any time t large enough, the last p vertices of your ham. path can be the selected subset there with some ε probability.
We had the same idea, you would be a bit disappointed looking at our solution though...
It produces an order in which problem i is more preferred than problem i+1 (maybe indirectly). Even if i+1 is more preferred than i in some other way, it doesn't really matter since there's a "plausible" chance i will be selected once again.
Is the multipoint evaluation and divide and conquer on the tree required in the expected solution? I didn't find any more clever way to solve it.
Very nice problems, thank you!
How to solve G ?
Let f(i, x) be the length of LIS of a1, a2, ..., ai that contains only integers up to x. Similarly, let g(i, x) be the length of LIS of ai + 1, ai + 2, ..., an that contains only integers larger than x.
For each i, you want to find the maximum of f(i, x) + g(i + k, x). You can maintain a segment tree of these sums for all x, then moving i forward by 1 can be done with O(1) modifications.
Thanks for nice problems :)
How to solve D? Using some clever trick of power series?
Just some typical tricks. Let A(x) be the GF of numbers.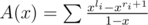 .
.
The answer should be
The last four terms can be calculated by brute forces. The time complexity is O(n3).
The first term can be calculated by "meet in middle". This part is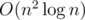 .
.
Thanks for replying!
I couldn't figure out how to calculate s-th coefficient of the first term by "meet in middle" in that order... Would you give me the details of this part?
Let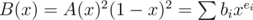 . The answer is
. The answer is  .
.
You can use the formula to split the binomial coefficients into two parts.
to split the binomial coefficients into two parts.
I have never thought about binomial coefficients with negative a... Now I can figure out the solution, thank you! :)
How to solve E? Some sort of integration?
Consider 10 lines that pass through two points. Roughly speaking, for each halfline, we are only interested in the direction of the halfline relative to these lines. Thus, essentially, there are only 20 choices for each halfline, and we can brute force all 205 combinations.
The only problematic situation is when we choose the same direction for multiple halflines. In this case, if we assign the same directions for k halflines, the probability that these halflines are disjoint is 1 / k!, so divide the probability by k!.
I don't have login id. Is there any other link from where i download problem set or can see problems?
Slightly unrelated question regarding moscode: If we've qualified (and it seems to be the case from what I could find that you count as qualified if you qualified for the world finals), is there any way to take it online, unofficially? I've tried to find a blog about moscode but could only find the one last year, so I hoped that I could get an answer here
You can participate in the Open Cup round.
How to solve J?
I don't know if there exists an easier/faster solution. A number is secondary, if and only if it has no subsequence equal to any number in 2,3,5,7,11,19,41,61,89,409,449,499,881,991,6469,6949,9001,9049,9649,9949,60649,666649,946669,60000049,66000049,66600049. Just match these numbers directly(in your digit DP). We will get a huge number of states, but only about 150000 are reachable, so we use a DFS to find them.
Another method: we construct a simple DFA for every number, and calculate the Cartesian product of them. Run DFA minimization on every product, so we can keep the number of states extremely small. I got a final DFA with 19 states.
How to solve C?
I have written a $$$\mathcal O(n\log^2 n)$$$ solution to A but I am still getting WA now.
This is my code
There is an editorial in Chinese.
I will try to explain my solution in English.
Firstly, we need to compute $$$\mathcal G(x)=\sum_{u\in \mathcal V} ue^{(|\mathcal V|-1)x}(1-\sum_{i=1}^{m_{u}}\mathcal F(|\hat{\mathcal T_i}|x))$$$, where $$$\hat{\mathcal T_i}$$$ means a subtree of $$$u$$$, $$$\mathcal F(x)=\frac{\sum_{j\geq \lfloor\frac{k}{2}\rfloor}\frac{x^j}{j!}}{e^{x}}$$$.
What we want to compute actually is $$$\sum_{i=1}^{m} b_if(a_ix)$$$.
We can compute it in $$$\mathcal O(n\log^2 n)$$$ by divide and conquer.
And then the answer when $$$k$$$ is an odd number is $$$\sum_{i=0}^k {n\choose i} i! [x^i]\mathcal G(x)$$$
When we want to compute the answer when $$$k$$$ is an even number, we can insert the node by the order of number. DSU is enough for us to compute the answer when the center is not unique.
Sorry for some typos.
wrong post sorry
How to solve C?
Oh maybe I've got it.
Consider a simple dp: $$$dp(i,l)$$$ means the number of tuples $$$(i,i+l-1,...)$$$. To calculate it, we need to know if $$$[i,i+l-1],[i+l,i+2l-1]$$$ have no more than 1 different position. If so, we call $$$i$$$ is good for $$$l$$$.
We assert that good positions form $$$O(\frac{n}{l})$$$ ranges. To find them, we use a method like what we do in BOI2004 Repeats(SPOJ687). We want to calculate LCP of 2 substrings allowing Hamming distance of 1, so use a suffix array to calculate LCP, ignore the first difference, and calculate LCP again. Then just do something similar to convolution.
After finding these ranges, you can use segment tree or
std::setto calculate the answer. The complexity is $$$O(n\log^2 n)$$$.