We decided to hold a mirror contest of yesterday's finals because there were several requests.
- Contest Link: https://atcoder.jp/contests/wtf19-open
- Start time: February 23rd (Sat), 23:00 JST
- Duration: 4 hours
This contest is unrated, but we want to keep it as fair as possible. Please do not participate in case you already know the problems (e.g., participants of Beijing camp), and do not discuss solutions with others during the contest.
This contest is recommended for reds and very ambitious oranges.











Link to standings of the official contest.
nutellas and very ambitious reds
Reminder, starts in 3 minutes
Nice problem E XD. Took me sth like 1 hour to verify answer to first sample xD.
Verifying the first sample is the main part of this problem, so you are very close.
Actually I did this in a bit different manner than in editorial. I got the interpretation with permutations, but didn't think about one with drawing from [0, 1] so my left and right parts weren't independent. Among others, I needed to calculate a weird sum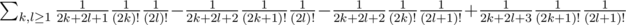 which turned out to be
which turned out to be 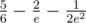 which was exactly what I wanted for first sample, but that didn't lead me to easy generalization to arbitrary patterns. I spend a lot more time on this problem than just verifying first sample and didn't even figure out how to compute appropriate sums for "one-sided patterns" (which show up when pattern contains two consecutive dashes) and computing them for the hardest testcases (which turn out to be just alternately X and -) seemed even much more complicated, so I wouldn't call that very close :P.
which was exactly what I wanted for first sample, but that didn't lead me to easy generalization to arbitrary patterns. I spend a lot more time on this problem than just verifying first sample and didn't even figure out how to compute appropriate sums for "one-sided patterns" (which show up when pattern contains two consecutive dashes) and computing them for the hardest testcases (which turn out to be just alternately X and -) seemed even much more complicated, so I wouldn't call that very close :P.
However I really like this problem, I love challenging probability/EV problems.
Can we see the codes submited by finallists?
My solution to C2, unfortunately a couple of times too slow (after some heavy optimizations, I'm now able to pass more than half of the max tests). I hope it's at least a tiny bit understandable:
Let's start with a solution to C1. Assume first that all lamps in the input have y ≥ 0. We use the operations in the statement to achieve the situation where the only lit lamps lie on the OX axis (y = 0). We can observe that each lamp (x, y) toggles all the lamps (x + t, 0) such that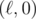 will remain.
will remain.
(y & t) == t. The input data in C1 asserts that after all such toggling exactly one lit lampThus we can write a fairly simple blackbox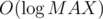 ). This allows us to compute the parity of the number of toggles to the left of any lamp (t, 0) in
). This allows us to compute the parity of the number of toggles to the left of any lamp (t, 0) in 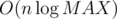 time. If this number is even, then the sought result is to the right of (t, 0); if it's odd, the result is to the left of (t, 0). We can binary search the result, and therefore we end up with a solution in
time. If this number is even, then the sought result is to the right of (t, 0); if it's odd, the result is to the left of (t, 0). We can binary search the result, and therefore we end up with a solution in 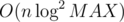 time.
time.
Parity(x, y, R)returning the parity of the number of lamps (t, 0), t ≤ R, that the input lamp (x, y) toggles (it can be done inHowever, we still need to consider the lamps with y < 0. To cope with this, let's pick M = 60 and let's move all the lamps up by 2M units (y' = y + 2M). C1 then asserts that there exists exactly one lamp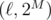 that produced the input data. We can however prove that this is equivalent to two lit lamps: at
that produced the input data. We can however prove that this is equivalent to two lit lamps: at 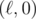 and
and 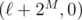 . Therefore, if we ask for the parity of the number of lamp toggles to the left of any lamp (t, 0), we will get an odd result iff
. Therefore, if we ask for the parity of the number of lamp toggles to the left of any lamp (t, 0), we will get an odd result iff 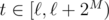 . This is a really wide interval, and it's easy to find any integer R belonging to it. Then we do an analogous binary search in [R - 2M, R].
. This is a really wide interval, and it's easy to find any integer R belonging to it. Then we do an analogous binary search in [R - 2M, R].
C2: we can't really use the parity that easily anymore. However, we still want to assume that all lamps fulfill y ≥ 0 (shift them up if they don't) and x ≥ 0 (shift them right so that it happens). We'll again toggle all the lamps so that the only lit lamps are lying on the OX axis, and we'll find the first lamp and the last lamp turned on after all the operations: (L, 0) and (R, 0). We can easily prove that in such a setup, the original single lamp must've been located at (L, R - L).
We'll generalize the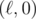 , \ell \leq R$, toggled by the input (x, y) lamp. Again, n invocations of such blackbox allow us to compute the
, \ell \leq R$, toggled by the input (x, y) lamp. Again, n invocations of such blackbox allow us to compute the 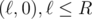 , that are on after all input lamps are processed. Using this, we can easily compute the first and the last turned on lamp using two binary searches.
, that are on after all input lamps are processed. Using this, we can easily compute the first and the last turned on lamp using two binary searches.
Parityblackbox. We'll assign each lamp (x, 0), x ≥ 0, a "random" p-bit number. Now we wantParity(x, y, R)to return thexorof all the numbers assigned to the lampsxorof all the numbers assigned to the lampsHow to produce sufficiently "random" numbers, though? Let's consider the finite field GF(2p) for some fairly large p (p = 32 should suffice). Generate a sequence of random elements of the field: (r0, r1, r2, ...). Now, each lamp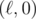 ,
, 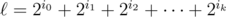 is assigned the value
is assigned the value 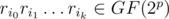 .
.  time. This allows us to implement the solution in
time. This allows us to implement the solution in 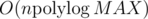 time; I believe it's
time; I believe it's 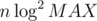 or
or 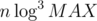 .
.
xorof the numbers translates to addition in GF(2p). I'm omitting a bunch of technical details right now, but it's now possible to implement theParityblackbox inHere is another solution to C2, due to lamejeck. At a glance it seems different from the one described above and the one in the editorial, but I'm not sure how different it really is.
Let's call a subset of the grid (equivalently, an assignmnet of numbers 0, 1 to every grid point) an annihilating pattern if it intersects each triangle {(x, y), (x, y + 1), (x + 1, y)} in an even number of points. (Personally, I think the situation becomes clearer if you think of the lamp configurations as forming a vector space over the field of two elements, where there is one basis vector for each lamp. An annihilating pattern is then a functional that vanishes at every triangle.) Anyway, given an annihilating pattern, we can determine if the point (X, Y) is in it just by counting the parity of the number of given points in the pattern.
The problem is now to find sensible annihilating patterns, that are both easy to compute, and give us useful information about (X, Y). If you fiddle with this, you will find lots of Sierpinski triangles. In particular, suppose we start with a periodic row that looks like ...0000100001..., i.e. 2k 0's followed by one 1. Filling in the rows above to make it annihilating, we get
Crucially the top row is just the second row from the bottom shifted one step to the left. So the rows are periodic with period 2k - 1, up to shifting. Now we can get rid of the row we started from, and just repeat the period, to get a very nice annihilating pattern. 'Hitting' the given points with this pattern and its left shifts requires O(n) bitset operations on bitsets of length 2k + 1, and lets us determine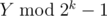 . Taking lcm of 2k - 1 from k = 2 to k = 13 gives 3.7e18, which is greater than 2e17+1, so if we consider this range of k's, then we can determine Y using CRT. Then we can determine X in the same way, or using the solution to C1. This solution uses O(n) operations on bitsets of length 8193, and turns out to be pretty fast.
. Taking lcm of 2k - 1 from k = 2 to k = 13 gives 3.7e18, which is greater than 2e17+1, so if we consider this range of k's, then we can determine Y using CRT. Then we can determine X in the same way, or using the solution to C1. This solution uses O(n) operations on bitsets of length 8193, and turns out to be pretty fast.