I'm looking for a good source with deep theory and practice problems about probability, doesn't matter if it is too math involved, and I would prefer one that is ACM-ICPC training oriented.... thanks in advance..
Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/21/2024 16:37:12 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I need help too!! Anyone? Also need help on game theory.
For game theory this is very helpful : www.math.ucla.edu/tom/Game_Theory/comb.pdf
It should be http://www.math.ucla.edu/~tom/Game_Theory/comb.pdf, and indeed that link seems to be interesting...
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=probabilities
I've read that topcoder article already, but it doesn't seem to be enough, at least for solving problems where you must deal with expectations on random variables...
What would be necessary to learn to solve this problem? http://www.codechef.com/ACMAMR12/problems/MINMAX
Nothing special , it just requires the basic definition of expected number and some about polynomial addition,multiplication and integration .
How do you get the polynomials? I was able to doing only with two variables, by integrating over areas, but for more variables I didn't know what to do.
I will try to explain my solution (though it seems more complex after I see others' solution.) Suppose you have to find the expected value of an expression ,say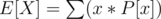
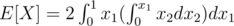
M = Max(x1,x2)
Then ,from the definition we have
Assume M = x , then we have to find the probability that value of M is x.
This will be when one of x1 OR x2 is equal to x , and the other has a value less than x. So
Hence , E[X] = 2 / 3 .This was the case of simple two variables.
Now come to the general case , we want the probability of the operator at the root , such that value after that is x .
Consider this as a state F(node , {either 0,1,2}) , here 0 means that we have to find probability such that it has value equal to x , 1 means to find less than x , 2 means to find greater than x . Now our answer is (root,0) .
The transition for example is like :
Suppose expression is : MmxxMxx , then at the root we have Maximum(a,b) operator and we want prob for being equal ,so answer will be:
(F(root->left,0)*F(root->right,1) + F(root->left,1)*F(root->right,0)) . Here F(node,{0,1,2}) will be a polynomial.
This is because either left value will be equal to x or right , and in either cases the other one will have value less than x.
For base case , if we have a leaf and we have to calculate F(leaf,0) then it is 1 , for F(leaf,1) it is x , for F(leaf,2) it is (1-x) .