Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> a;
inline bool read() {
if(!(cin >> n))
return false;
a.resize(n);
for(int i = 0; i < n; i++) {
cin >> a[i];
a[i]--;
}
return true;
}
inline void solve() {
int cnt = 0, pos = 0;
while(pos < n) {
cnt++;
int mx = pos;
while(pos < n && pos <= mx) {
mx = max(mx, a[pos]);
pos++;
}
}
cout << cnt << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
#endif
if(read()) {
solve();
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (Roms)
#include <bits/stdc++.h>
using namespace std;
int t, n;
string s;
int main(){
cin >> t;
for(int tc = 0; tc < t; ++tc){
cin >> n >> s;
int res = n - 1;
for(int i = 0; i < n; ++i)
if(s[i] == '>' || s[n - 1 - i] == '<')
res = min(res, i);
cout << res << endl;
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (Roms)
#include <bits/stdc++.h>
using namespace std;
const int N = 300009;
int n, k;
pair<int, int> a[N];
int main() {
cin >> n >> k;
for(int i = 0; i < n; ++i)
cin >> a[i].second >> a[i].first;
sort(a, a + n);
long long res = 0;
long long sum = 0;
set<pair<int, int> > s;
for(int i = n - 1; i >= 0; --i){
s.insert(make_pair(a[i].second, i));
sum += a[i].second;
while(s.size() > k){
auto it = s.begin();
sum -= it->first;
s.erase(it);
}
res = max(res, sum * a[i].first);
}
cout << res << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
int main() {
int n; cin >> n;
long long ans = 0;
for(int id = 2; id < n; id++)
ans += 1ll * id * (id + 1);
cout << ans << endl;
}
1140E - Palindrome-less Arrays
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define x first
#define y second
typedef long long li;
typedef pair<int, int> pt;
const int MOD = 998244353;
int norm(int a) {
while(a >= MOD) a -= MOD;
while(a < 0) a += MOD;
return a;
}
int mul(int a, int b) {
return int(a * 1ll * b % MOD);
}
int n, k;
vector<int> a;
inline bool read() {
if(!(cin >> n >> k))
return false;
a.resize(n);
fore(i, 0, n)
cin >> a[i];
return true;
}
pair<int, int> calc(int len) {
if(len == 0) return {0, 1};
if(len & 1) {
auto res = calc(len >> 1);
return {norm(mul(res.x, res.x) + mul(k - 1, mul(res.y, res.y))),
norm(mul(2, mul(res.x, res.y)) + mul(k - 2, mul(res.y, res.y)))};
}
auto res = calc(len - 1);
return {mul(k - 1, res.y), norm(res.x + mul(k - 2, res.y))};
}
vector<int> curArray;
int calcSeg(int l, int r) {
if(r >= sz(curArray)) {
int len = r - l - 1, cf = 1;
if(l < 0)
len--, cf = k;
if(len == 0) return cf;
auto res = calc(len - 1);
return mul(cf, norm(res.x + mul(k - 1, res.y)));
}
if(l < 0) {
if(r - l == 1) return 1;
auto res = calc(r - l - 2);
return norm(res.x + mul(k - 1, res.y));
}
auto res = calc(r - l - 1);
return curArray[l] == curArray[r] ? res.x : res.y;
}
inline void solve() {
int ans = 1;
fore(k, 0, 2) {
curArray.clear();
for(int i = 0; 2 * i + k < n; i++)
curArray.push_back(a[2 * i + k]);
int lst = -1;
fore(i, 0, sz(curArray)){
if(curArray[i] == -1) continue;
ans = mul(ans, calcSeg(lst, i));
lst = i;
}
ans = mul(ans, calcSeg(lst, sz(curArray)));
}
cout << ans << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
if(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
1140F - Extending Set of Points
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
typedef long long li;
#define x first
#define y second
const int N = 300043;
const int K = 300000;
int p[2 * N];
int s1[2 * N];
int s2[2 * N];
li ans = 0;
int* where[80 * N];
int val[80 * N];
int cur = 0;
void change(int& x, int y)
{
where[cur] = &x;
val[cur] = x;
x = y;
cur++;
}
void rollback()
{
cur--;
(*where[cur]) = val[cur];
}
int get(int x)
{
if(p[x] == x)
return x;
return get(p[x]);
}
void merge(int x, int y)
{
x = get(x);
y = get(y);
if(x == y) return;
ans -= s1[x] * 1ll * s2[x];
ans -= s1[y] * 1ll * s2[y];
if(s1[x] + s2[x] < s1[y] + s2[y])
swap(x, y);
change(p[y], x);
change(s1[x], s1[x] + s1[y]);
change(s2[x], s2[x] + s2[y]);
ans += s1[x] * 1ll * s2[x];
}
void init()
{
for(int i = 0; i < K; i++)
{
p[i] = i;
p[i + K] = i + K;
s1[i] = 1;
s2[i + K] = 1;
}
}
vector<pair<int, int> > T[4 * N];
void add(int v, int l, int r, int L, int R, pair<int, int> val)
{
if(L >= R) return;
if(L == l && R == r)
T[v].push_back(val);
else
{
int m = (l + r) / 2;
add(v * 2 + 1, l, m, L, min(R, m), val);
add(v * 2 + 2, m, r, max(m, L), R, val);
}
}
li res[N];
void dfs(int v, int l, int r)
{
li last_ans = ans;
int state = cur;
for(auto x : T[v])
merge(x.x, x.y + K);
if(l == r - 1)
res[l] = ans;
else
{
int m = (l + r) / 2;
dfs(v * 2 + 1, l, m);
dfs(v * 2 + 2, m, r);
}
while(cur != state) rollback();
ans = last_ans;
}
int main()
{
int q;
scanf("%d", &q);
map<pair<int, int>, int> last;
for(int i = 0; i < q; i++)
{
int x, y;
scanf("%d %d", &x, &y);
--x;
--y;
pair<int, int> p = make_pair(x, y);
if(last.count(p))
{
add(0, 0, q, last[p], i, p);
last.erase(p);
}
else
last[p] = i;
}
for(auto x : last)
add(0, 0, q, x.y, q, x.x);
init();
dfs(0, 0, q);
for(int i = 0; i < q; i++)
printf("%I64d ", res[i]);
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
typedef long long li;
#define x first
#define y second
const int N = 600043;
li d1[N];
li d2[N][2];
li dist_temp[N][2];
vector<pair<int, int> > g[N];
vector<int> qs[N];
int qq[N][2];
li ans[N];
int n;
int used[N];
int cnt[N];
int last[N];
int cc = 1;
void preprocess()
{
set<pair<li, int> > q;
for(int i = 0; i < n; i++)
q.insert(make_pair(d1[i], i));
while(!q.empty())
{
int k = q.begin()->second;
q.erase(q.begin());
for(auto e : g[k])
{
int to = e.first;
li w = d2[e.second][0] + d2[e.second][1];
if(d1[to] > w + d1[k])
{
q.erase(make_pair(d1[to], to));
d1[to] = w + d1[k];
q.insert(make_pair(d1[to], to));
}
}
}
}
void dfs1(int x, int p = -1)
{
if(used[x]) return;
cnt[x] = 1;
for(auto y : g[x])
{
int to = y.first;
if(!used[to] && to != p)
{
dfs1(to, x);
cnt[x] += cnt[to];
}
}
}
vector<int> cur_queries;
pair<int, int> c;
int S = 0;
void find_centroid(int x, int p = -1)
{
if(used[x]) return;
int mx = 0;
for(auto y : g[x])
{
int to = y.first;
if(!used[to] && to != p)
{
find_centroid(to, x);
mx = max(mx, cnt[to]);
}
}
if(p != -1)
mx = max(mx, S - cnt[x]);
c = min(c, make_pair(mx, x));
}
void dfs2(int x, int p = -1, int e = -1)
{
if(used[x]) return;
if(p == -1)
{
dist_temp[x * 2][0] = dist_temp[x * 2 + 1][1] = 0ll;
dist_temp[x * 2][1] = dist_temp[x * 2 + 1][0] = d1[x];
}
else
{
for(int k = 0; k < 2; k++)
{
li& D0 = dist_temp[x * 2][k];
li& D1 = dist_temp[x * 2 + 1][k];
D0 = dist_temp[p * 2][k] + d2[e][0];
D1 = dist_temp[p * 2 + 1][k] + d2[e][1];
D0 = min(D0, D1 + d1[x]);
D1 = min(D1, D0 + d1[x]);
}
}
for(auto y : qs[x])
{
if(ans[y] != -1) continue;
if(last[y] == cc)
cur_queries.push_back(y);
else
last[y] = cc;
}
for(auto y : g[x])
{
int to = y.first;
if(!used[to] && to != p)
dfs2(to, x, y.second);
}
}
void centroid(int v)
{
if(used[v]) return;
dfs1(v);
S = cnt[v];
c = make_pair(int(1e9), -1);
find_centroid(v);
int C = c.second;
used[C] = 1;
for(auto y : g[C])
centroid(y.first);
cc++;
cur_queries.clear();
used[C] = 0;
dfs2(C);
for(auto x : cur_queries)
{
int u = qq[x][0];
int v = qq[x][1];
ans[x] = min(dist_temp[u][0] + dist_temp[v][0], dist_temp[u][1] + dist_temp[v][1]);
}
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%I64d", &d1[i]);
for(int i = 0; i < n - 1; i++)
{
int x, y;
li w1, w2;
scanf("%d %d %I64d %I64d", &x, &y, &w1, &w2);
--x;
--y;
d2[i][0] = w1;
d2[i][1] = w2;
g[x].push_back(make_pair(y, i));
g[y].push_back(make_pair(x, i));
}
int q;
scanf("%d", &q);
for(int i = 0; i < q; i++)
{
scanf("%d", &qq[i][0]);
scanf("%d", &qq[i][1]);
--qq[i][0];
--qq[i][1];
qs[qq[i][0] / 2].push_back(i);
qs[qq[i][1] / 2].push_back(i);
}
preprocess();
for(int i = 0; i < q; i++)
ans[i] = -1;
centroid(0);
for(int i = 0; i < q; i++)
cout << ans[i] << endl;
}










51769222 this is my submission for problem c why is it giving wrong answer
Because long somtimes is just int. So to prevent this mistake everytime write "long long". UPD: When you think int isn't enough
In Problem D, yes I got AC with greedy solution but How to Do using DP (recursive approach)
At first during contest i started to solve this question as top down dp(recursive), but i was not able to solve.. can someOne give there dp recursive solution..
dp[3]=6 dp[i]=dp[i-1]+(i*(i-1)) dp[N] is the answer. Hope that helps
@bhatnagar.mradul bro u are trying to implement that greedy solution using dp.. i dont mean that..
i want to know that O(n^3) solution using recursive dp
I used O(N^2) dp
dp[i][j] means answer for polygon that is made from this points -> [1,2...i] and [n,n-1,...j].
dp[i+1][j]=min(dp[i+1][j],dp[i][j]+i*(i+1)*j)
dp[i][j-1]=min(dp[i][j-1],dp[i][j]+i*(j-1)*j)
You need to update answer when i+1==j-1.
My solution.
:\
Keep two pointers as state. dp[i][j] should have the optimal total cost of triangulation of the polygon with { i, i+1, i+2, ..., j-1, j } vertices. To calculate dp[i][j] you have to take the line i-j at some point in a triangle. Pick a vertex k such that i < k < j and make a triangle { i, j, k }.
So dp[i][j] = min { i*j*k + dp[i][k] + dp[k][j] } for all k such that i < k < j.
Result is dp[1][n]. Code if needed.
can F be solved with sqrt-dynamic connectivity trick?
I tried, but I haven't managed to squeeze my $$$O(q^{1.5})$$$ implementation in time limit. But it doesn't mean that it's impossible, considering my optimization skills.
Sometimes actually $$$O(q^{1.5} \log q)$$$ version can be faster, maybe I'll try that.
can I find any tutorial for that ?
Problem C, editorial:
multiset, because two songs can be equalyou can insert pair, with second equal to index, this guaranties uniqueness.
In problem E, What is the difference between l is odd and l is even ? I think the way to compute cntDiff and cntSame when l is odd is similar when l is even ?
when l is odd then (**#**) you can't split it into tow same segment . the different of those just that .
I mean we can use recipe when l is even for both case,can't we?
You can, but it will drop complexity from $$$O(\log{l})$$$ to $$$O(l)$$$. It doesn't matter in this specific task, but it worse overall.
can anyone explain the problem E , i didn't understood the editorial
If you have palindrome of size ODDNUMBER, you also have palindrome of size ODDNUMBER — 2. So you just avoid palindromes of length 3 and that's enough.
Split the array A into two smaller arrays ODD and EVEN, odd indices goes into ODD, even indices go into EVEN. You want to answer this question:
"How many ways are there to fill in -1, so that no adjacent numbers are the same"
Solve that question for the two arrays, final answer is simply solve(EVEN)*solve(ODD)
For the solution of problem C, what if the erased item from the set is actually the one just inserted? e.g., suppose we insert one a[i] that has the smallest beauty as well as the shortest length, and if the set size exceeds k, the element that will be popped out will be a[i]. But at the end of this iteration, we compute the score by a[i].first still, which is formally wrong.
But this may not cause trouble: since sum doesn't change in this case, and a[i].first should be smaller than any song in the set, so that a[i].first * sum <= min_beauty(s).first * sum; this implies that the maximal value won't be polluted by a[i].first * sum, and the actual score has been considered.
Great observation!
can u please give some mathematical proof of C.. that is why we sort on the basis of beauty.. in my opinion if we multiply beauty and length and then sort is it work???.... plz help me?? I can't understand...Thanks
That's exactly what the editorial for C is missing I suppose. PS: I know I'm late.
Probably the best solution for Problem D. here:- https://codeforces.com/contest/1140/submission/51801930
Approach For n = 3 the cut will 1-3. ans = 1*2*3
For n = 4 the cuts will be 1-3, 1-4. ans = 1*2*3 + 1*3*4
for n = 5 the cuts will be 1-3, 1-4, 1-5. ans = 1*2*3 + 1*3*4 + 1*4*5
If we look at the pattern then for n = N, the ans will be 1*2*3 + 1*3*4 + 1*4*5 + 1*5*6 + ... + 1*(N-1)*(N) which can be written as sum from n = 2 to N : n(n+1)
changing limit of n from 2 to 1, we need to subtract 1*2, i.e 2 from the result
(sum from n = 1 to N : n(n+1) )- 2 (sum from n = 1 to N : n^2 + n) — 2
sum from n = 1 to N : n^2 = (n(n+1)(2n+1))/6 sum from n = 1 to N : n = (n(n+1))/2 ans = (n(n+1)(2n+1))/6 + (n(n+1))/2 — 2;
ans = (n(n+1)(n+2))/3 — 2;
all you need to do is take the input n, decrement n by 1; ans use the above formula.
Time Complexity — O(1) Space Complexity — O(1)
.
Can anybody please explain G's solution? I'm not getting the editorial.
First we need to find the shortest path between nodes of the form $$$2i-1$$$ to $$$2i$$$. This can be done with a dp on the tree. Notice that any such shortest path will only take one edge between the even tree and the odd tree. Simply replacing the cross edge distance will not change shortest distances, and will make reasoning through the problem easier.
Next to find shortest paths, if you use centroid decomposition we can find shortest path from root to a node by:
dp[i][j]defined to be the length of the shortest path from node $$$2i-j$$$ to the root with another tree dp.If you use binary jumping, you can use: -
dp[i][j][k][l]defined to be the the distance from $$$2i-j$$$ to the $$$2^l$$$ th ancestor in either the even or odd tree (kept track of by k).I personally find binary jumping easier. Either way, this uses the critical observation that if you want to find the path from one node to another, you need to pass through the simple path on the tree between the two nodes (possibly jumping back and forth between the trees).
I believe this part can be simplified a bit. Write the usual dynamic
dp[n][k]and notice that we actually need only 2 states instead of k:dp[i][j == a]anddp[i][j != a]In Problem E, How do we get cntSame(0) = 0 and cntDiff(0) = 1 and how this relation is coming out when l is even or odd. Can someone explain with example.
cntSame(0) = 0 since there is no way to make 'aa' have all pairs of consecutive elements are distinct. cntDiff(0) = 1 since there is one way to make 'ab' have all pairs of consecutive elements are distinct.
Why don't precompute values cntSame and cntDiff for every 1<=i<=n in O(n) using dp?
In F, it says "...using path compression in DSU here is meaningless...". Is it meaningless? I think it can actually make the solution slower, since path compression is amortized, and if the structure allows undoing operations, then amortization should fail (might give TLE on countertests).
In problem E, there is no need to make separate recurrence relation for odd and even lengths as mentioned in the tutorial. The one for even length is enough to get for the odd length.
cntSame(l)=(k−1)⋅cntDiff(l−1)
cntDiff(l)=cntSame(l−1)+(k−2)⋅cntDiff(l−1).
link to the code
Sorry to bother you, could you explain how did you get that recurrence on problem E? I'm having trouble on find it.
theProcess Consider a -1 -1 ...ltimes... -1 -1 b
You need to find the no. of arrays in which no two consecutive elements are equal.
So first if you assign the value to the lth "-1" element i.e. element before b, obviously you can assign all the values to it from 1 to k, except b. You can't assign b to it because no two consecutive elements should be equal. So there are (k-1) ways in which you can assign the value to lth "-1" element.
Now I hope you know the meaning of cntSame(l), and cntDiff(l).
To calculate cntSame(l), consider what happens when a=b.
Suppose you assign value to p to the lth "-1" element. Obviously, p!=b.
Since a=b, therefore p!=a. So, remaining number of values will be (k-1) i.e. except a(or b, since a=b). Therefore cntSame(l) = (k-1)*cntDiff(l-1)
To calculate cntDiff(l), consider what happens when a!=b.
Suppose you assign value to p to the lth "-1" element. Obviously, p!=b.
Since a!=b, You can either assign p=a or p!=a. There will be exactly one case to assign p=a and (k-2) cases to assign p!=a. (k-2 because you cannot also assign p=b)
Therefore cntDiff(l) = cntSame(l-1) + (k-2)*cntDiff(l-1)
Thanks for the help arjitkansal!
I read many solutions for problem E. What I understood is we have to find continuous sequences of -1 for even and odd positions separately and apply recurrence to calculate number of ways such that consecutive numbers should be different and multiply results for both even and odd positions. What I didn't understood is how numbers other than -1 affect the total number of ways and how recurrence works for them. Can anyone please explain it ?
In problem C When we sliding the window for the sum of length, shouldn't we include the current element with least beauty value? I mean, what we're really finding is the most (k-1) elements we've searched before but not k because the length of ith one is included must?
https://codeforces.com/contest/1140/submission/52462663
yes the length of the i'th one must be included.
so the idea is to consider every i'th element as the minimum beauty. for this we sort the songs in descending order of beauty. so the first song we consider will have the highest beauty. (what if 2 songs have same beauty? read last 2 para)
we will at all times try to maintain a list of songs of size at most k. this list will contain at most k songs with the highest length, not including the current i'th song. so if we already have a list of size k, then we remove the song with the smallest length. so size become k-1. then we include the current song into the list, size becomes k, and update our maxTillNow. if out list is less than k, then we just simply include the song and update maxTillNow.
to maintain this list we will use a priority_queue (min heap), where the top element is the song with the smallest length. this way we don't need to keep track of song indexes.
while sorting our list of songs in descending order of beauty, if 2 songs have the same beauty we place the song with the smaller length first (this is very important). this is because when we consider the i'th beauty, obviously the i'th length must also be included. which means, if there is already a song in the list with the same beauty as our current minimum beauty we need to pick the one with the smaller length to discard.
this process becomes easier to deal with for 2 or more songs with same beauty, if we consider the song with the greater length as late as possible. because the song with the smaller length will already be in the list, so we can simply discard it and include the current song.
read code for more clarity.
Can anyone tell the complexity of the for loop dealing with set in C?
only 1 time loop will execute for each outer loop. So we could have used if condition (instead of iterating over set) as well because at a time, its gauranteed, set size can only be 'k' at max, since we are increasing set size by 1 in each outer loop iteations.
why I don't understand the Problem B.I think the answer of string "<<<<>>>>" should be 1,because we can do some operations,finally the string will be "<>",then the answer is 1 .
You may remove some characters from the string before applying the operations.
Oh,thank you very much
In problem C,I cannot understand why the does the set use pair<int,int> instead of int .In other words,if I submit my code with set 《int》 ,then I will wrong on test 3 .It seems that we haven't utilize the second of the pair<int,int>. Sorry for my poor English.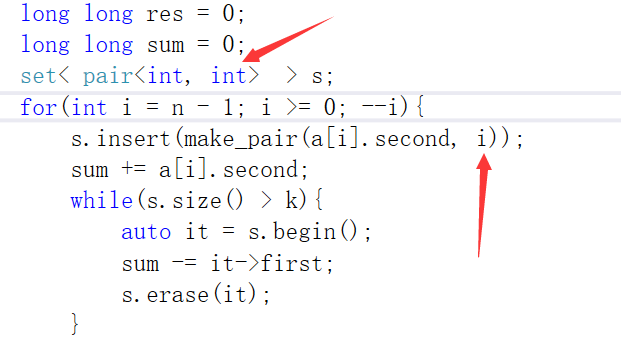
Set does not contain duplicate elements. but we need to store it. pair<int,int> is used for this reason. Because index itself is stored with the beauty value, there is no chance for duplicate elements.
Oh,I understand.Thank you for solving my problem.
My opinion may be subjective, but problem A was very poorly written and hard to comprehend exactly what is being asked.
https://codeforces.com/contest/1140/submission/83237143 what is wrong in my sol (Div2 C)
In problem C when I used set st it wont work but if I use set<pair<int,int>>st it does work
Set does not contain duplicate elements. but we need to store it. pair<int,int> is used for this reason. Because index itself is stored with the beauty value, there is no chance for duplicate elements.(copied)
in 1140C can anybody tell what is the use making PAIR there. its giving wrong answer of 3rd testcase if I am not making a paired set.
I'm a bit confused on problem G's solution. As an example, on a normal tree, how could we precompute the distance from each centroid to every node in its centroid decomposition subtree? I can think of a brute force $$$O(nlog^2_2n)$$$ solution using a method like binary jumping and precomputing all the possibilities, but this pretty much defeats the purpose of using centroid decomposition to solve this problem. Is there some sort of efficient $$$O(nlog_2 n)$$$ DFS solution that I'm missing? Thanks in advance
Edit: I figured it out already
In C , for each bi we are taking max k possible values , so that our answer = bi*(max sum of those k values )
But, what we if chosen k playlist don't contain the current beauty bi, eg : k==3 b1 b2 b3 ... t1 t2 t2.... for b1 : answer : b1*( t2+t3+t5) // assume t2, t3, t5 have max ti then, we actually haven't choose the first playlist , as we are not considering its ti values Can someone explain me where i am getting wrong ?