This problem is hard because it might be impossible to consider a dynamic programming solution carefully and finally find the mystery.
Let dp[i][j]=(the minimum transformation price to the moment if y1... yi have been determined and yi = j).
It's easy to find that:
dp[1][p] = (p - x1)2
f[i][p] = min(dp[i - 1][q] | p - b ≤ q ≤ p - a)
dp[i][p] = (p - xi)2 + f[i][p]
Solutions using this idea straight can't pass because it needs very huge amount of memory and time(in fact it's infinite). So we should consider the problem more accurately.
Here comes the magic: let dp[i] be a function for p.
First of all, we'll use the monotonicity of its derivative dp[i]' and mathematical induction to prove that dp[i] is a strictly unimodal function. More strongly, we can prove dp[i]' is a strictly increasing function.
dp[1]'(p) = 2(p - x[1]). Obviously so it is.
If we have proved that dp[i]' is a strictly increasing function, and min dp[i] = dp[i](k). In addition, dp[i]'(k) = 0.
For f[i + 1] at this moment:
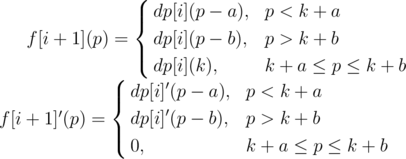
Notice that for the derivative, actually what we do is to cut dp[i]' at the place p = k, and then the left part (p ≤ k) moves to the right a units while the right part (p ≥ k) moves to the right b units. After this operation, the gap (k + a... k + b) is filled by 0 so that it's still a continuous function.
We can find f[i + 1]' is also a increasing function but not strictly. Then dp[i + 1]'(p) = 2(p - xi + 1) + f[i + 1]'(p), now it's absolutely a strictly increasing function.
Since we have proved any dp[i] is a strictly unimodal function, we can push xi one by one and calculate the function dp[i] immediately.
Let's focus on the operation to dp[i]':
Step 1. Determine k for dp[i]'(k) = 0.
Step 2. Cutting, translation, and filling 0.
Step 3. Add a linear function 2(p - xi).
Because of step 2, the derivative is in reality a piecewise function, and any part of this function is a linear function. Besides, there are at most O(n) parts.
Finally, We can use a simple array to hold all the endpoints. Since we should maintain at most O(n) endpoints for n times, the time complexity is O(n2).
Hint 1.
If you read the solution in earnest, you may have some questions.
Q: Why can't I use ternary search for every k?Or even binary search?
A: It's obviously right, but the time complexity is O(n2s) where s is times for the search. Either it will get TLE or the precision is not enough.
Just like this :) Questions are welcomed.
Hint 2.
Can we go beyond O(n2)?
Yes of course, by using some advanced data structures like a balanced tree with lazy tags. It's time for you to aftertaste and think more.
UPDATE
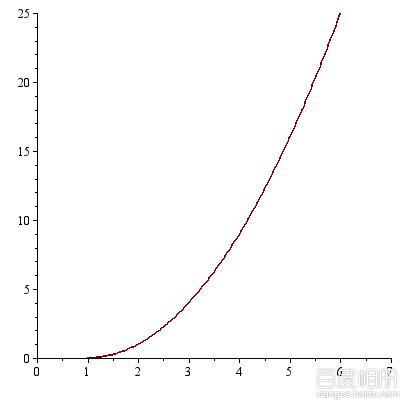
Figures from CMHJT for the input(not the sample input):
3 6 1 2
1 4 6
dp[1]:
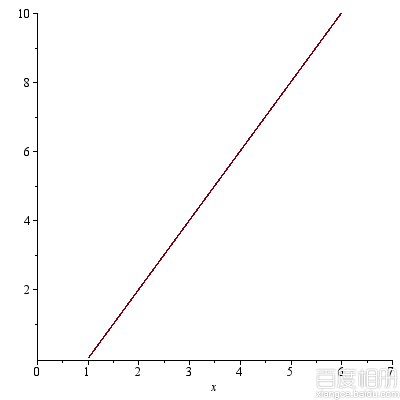
dp[1]':
dp[2]:

dp[2]':

dp[3]:

dp[3]':

You can visually see that the minimum price is  when
when 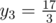











Am I supposed to write a article to get more contribution?
Hah……in fact I cannot keep in touch with xiaodao……
To everyone: he is just joking~But if it still didn't appear,CF #173's editorial would come first. Too bad,wasn't it? I spent all my morning to write them with an English-Chinese Online Dictionary. If I did't do this I'd like to wake up just now~
Oh, come of it, #171's editorial is absent right now after all ... I won't allow such things happened .. .
GJ.nice translation
I have a different approach that is O(n^2) 3313283. Here's the comment from the start of my program, which is written in ocaml. :-)
It's a DP algorithm. Keep y_opt.(i) which is the natural place where the point y.(i) will land when considering only points 0, 1, 2... i.
To compute y_opt.(i) we assume we have already computed the previous ones. What we do now is see if y.(i) acting alone would be within the window defined by y_opt.(i-1). If it is, we're done with y_opt.(i). Say y.(i) is too high to be compatible with y_opt.(i-1). Then we glue these two points together by asserting y.(i)-y.(i-1)=b. (Analogously, if y.(i) is too low compared to y_opt.(i-1) we assert y.(i)-y.(i-1)=a instead.) This pair of points has a natural position uninfluenced by anything outside of them. If this position is compatible with y_opt.(i-2) then we're done, otherwise we add y.(i-2) to the chain and continue. So the elements are chained together by a sequence of as and bs, intermixed.
We can prove by induction that the solution that this finds is optimal. The base case is when y.(i) is within the window allowed by y_opt.(i-1). Clearly this is the right answer. Now suppose that we have established that in the optimal solution some chain of differences relating y.(k),...,y.(i-2), y.(i) must occur. This means that when searching for the optimal solution we need only consider these values moving in lockstep as specified by the chain. Looking at point k-1 if the chain is too low, then the optimal solution must also have y.(k-1) in the chain being a below y.(k), and if point k-1 is too high then it must be in the chain b below y.(i). (The intuition is that of a spring. If you move your finger toward a spring and you touch the spring, pushing harder on the spring will keep your finger in contact with the spring. The spring will not suddenly pull away from your finger as you push harder. The (x-y)^2 cost function ensures that this is the correct model.)
So the algorithm is O(n^2). It might be possible to work out a version of this algorithm that is O(n log n) by keeping the chains in a search tree. Then instead of starting from scratch each time when adding a new point, it would edit the current chain. It is not clear that this can be made to work.
Wow, that one is really awsome!
Emmm, I am wondering whether your method works in such a case:
n = 60000 a = b = 1 q = 10^9 x[i] = (i + 1) * 3
It seems that your method would use strictly O(n^2) time.
It's a subtle solution! But its O(nlogn) implementation seems to be a little messy...