Hi, Here's the editorial.
Please note that not all the codes presented below belong to me. (It's a combination of codes from our problemsetters and testers) -- And I borrowed AKGMA's account since I wasn't able to link to my own submissions somehow!
Note: It seems that the Codeforces mark-up is not functioning. To see a submission go to: http://www.codeforces.com/contest/282/submission/submission-number
A: Bit++
Just use a simple loop. (Take a look at the Python code)
GNU C: 3314471
Python: 3314475
B: Painting Eggs
This one can be solved by a greedy algorithm. Start from the 1st egg and each time give the egg to A if and only if giving it to A doesn't make the difference > 500, otherwise give it to G.
To prove the correctness, one can use induction. The base case is trivial. Suppose that we've assigned the first n - 1 eggs such that the total money given to A is Sa and total money given to G is Sg. We can assume Sa ≥ Sg. Now we must either add gn to Sg or add an to Sa. If we can't add gn to Sg, then Sg + gn > Sa + 500, so - 500 > Sa - Sg - gn, adding 1000 to both sides gives us the inequality 500 > Sa + (1000 - gn) - Sg which is exactly what we need to make sure that we can add an = 1000 - gn to Sa.
GNU C: 3314488
Python: 3314492
C: XOR and OR
First of all, check the length of the two strings to be equal. Then with a little try and guess, you can find out that the zero string (00...0) can't be converted to anything else and nothing else can be converted to zero. All other conversions are possible.
GNU C++: 3314503, 3314504, 3314509, 3314512, 3314514
D: Yet another Number Game
For n=1, everything is clear. If a1 = 0 then BitAryo wins, otherwise BitLGM is the winner.
For n=2: define win[i][j] = (Whether i,j is a Winning position). It's easy to calculate win[i][j] for all i and j, using a loop (Checking all possible moves). This leads us to an O(n3) solution.
For n=3: Everything is similar to NIM, With the same statement of proof as for NIM, i,j,k is a winning position if and only if (i xor j xor k) ≠ 0.[Don't forget the parentheses in code :) ] Complexity: O(1)
One can also solve this case using DP. We define lose[i][j]= (Least k, such that i,j,k is a losing position) ,lose2[i][j]=(Least k, such that k,k+i,k+i+j is a losing position) and win[i][j][k] just as the case with n=2. As in the codes below, one can calculate all these values in O(n3).
Using the same DP strategy for n=2 and the O(1) algorithm for n=3 and n=1, leads us to a total complexity of O(n2) which was not necessary in this contest.
GNU C++: 3314578, 3314580, 3314585, 3314588
E: Sausage Maximization
Can be solved using a trie in O(n log (max{ai})).
Start with a prefix of size n, and decrease the size of prefix in each step. For each new prefix calculate the XOR of elements in that prefix and add the XOR of the newly available suffix (which does not coincide with the new prefix) to the trie, then query the trie for the best possible match for the XOR of the new prefix. (Try to get 1 as the first digit if possible, otherwise put 0, then do the same thing for the second digit and so on). Get a maximum over all answers you've found, and it's all done. [By digit, I mean binary digit]
We hope you enjoyed the tasks.











There is O(1) solution for D problem. For n = 2 every losing position follow a regular pattern determined by the golden ratio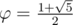 . For any
. For any 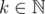 losing numbers are nk = ⌊ kφ ⌋ and mk = ⌊ kφ2⌋.
losing numbers are nk = ⌊ kφ ⌋ and mk = ⌊ kφ2⌋.
How do you prove it?
http://math.rice.edu/~michael/teaching/2012Fall/Wythoff.pdf
in problem D: for n = 3: in order to say that this problem is the same as Nim we have to prove that: if (i ^ j ^ r) = 0 then ((i-k) ^ (j-k) ^ (r-k)) != 0 for (k > 0) how do we prove this??
.
please hyperlink the solutions!
in problem D: for n = 3: in order to say that this problem is the same as Nim we have to prove that: if (i ^ j ^ r) = 0 then ((i-k) ^ (j-k) ^ (r-k)) != 0 for (k > 0) how do we prove this??
edited
fixed
I was wrong
let's try induction on number of bits :D
statement : for every i, j, r and k>0 and k<=min(i, j, r). if (i ^ j ^ r) = 0 then ((i-k) ^ (j-k) ^ (r-k)) != 0.
basis : for n == 2, the only case is ("11", "10", "01") and only k is 1 -> "10" xor "01" xor "00" = "11"
hypothesis : if most valuable bit of three number that's not 0 is smaller or equal n then ((i-k) ^ (j-k) ^ (r-k)) != 0.
inductive step : n+1 'th bit in exactly two of three numbers is equal 1, consider that numbers are i and j. if this bit in (i-k) and (j-k) is equal 1 we can skip this bit from number, else if this bit in one of (i-k) and (j-k) is equal 1 statement is correct for n+1, else if this n+1 'th bit in both (i-k) and (j-k) is equal 0 so we can skip this bit in i and j and k and by hypothesis the statement is proofed
First of all,thank you for giving me inspiration,i think it's easy to understand this.We know 0<k<min(i,j,r),then consider an optional position in k which is 1.And consider this position in i,j,r .There are two case. case 1: three 0 at this position in i,j,r. case 2: two 1 and one 0 at this position in i,j,r. In case one ,after subtraction there remain three 1.In case two ,after subtraction there remain two 0 and one 1. In both case ,(i-k)^(j-k)^(r-k) cannot be 0 .
.
I don't like the 'try and guess' part of C problem. So I'll try another explanation when the sizes of the strings are equal.
First look at the table:
This is the table with the operations and results. As we can see, when we try to convert to adjacent zeros, we receive two zeroes again (00 -> 00). Similarly, when one of the adjacent digits is 1, we receive atleast one 1 (10 -> 11, 01 -> 11, 11 -> 01 or 10). That means that we cannot receive two zeroes from 01, 10, and 11.
That's why when one of the string is consisted only with zeros and the other has at least one 1, the transformation is impossible.
The other conclusions are the following: 01 -> 11 -> 10 (1 is moved to the left) and 10 -> 11 -> 01 (1 is moved to the right). These transformations allow us to move ones whenever we want. 01 -> 11, 10 -> 11, 11 -> 01 or 10. The last transformations allow us to increase or decrease the number of ones as we like.
That means that we can reach any positive number of ones and we can arrange them whatever we like. So when the two strings have at least one 1 each, then the transformation is possible.
Of course, when the two string are consisted only with zeros, then there is no transformation needed, so the answer is YES.
i think by "try and guess". Author means to find a logic. ultimately you arrived at same conclusion. one can see how this is happening by finding pattern in between or by proving it manually .. it's all human :)
I agree with you. But more solutions proposed will help everyone to choose for himself.
nice solution..aRaGaR
Could anyone explain this test case for problem D ?
2
3 4
My solution is:
Case 1: BitLGM (LGM) decreases both numbers by 3: 3 4 => 0 1. BitAryo (Aryo) decreases 2nd number by 1 and wins: 0 1 => 0 0.
Case 2: LGM decreases 1st number by 1: 3 4 => 2 4. Aryo decreases 2nd number by 3: 2 4 => 2 1 => sample test #2
Case 3: LGM decreases 1st number by 2: 3 4 => 1 4. Aryo decreases 2nd number by 2: 1 4 => 1 2 => sample test #2
Case 4: LGM decreases 1st number by 3: 3 4 => 0 4. Aryo decreases 2nd number by 4 and wins: 0 4 => 0 0
Case 5: LGM decreases 2nd number by 1: 3 4 => 3 3. Aryo decreases both numbers by 3 and wins: 3 3 => 0 0
Case 6: LGM decreases 2nd number by 2: 3 4 => 3 2. Aryo decreases 1st number by 2: 3 2 => 1 2 => sample test #2
Case 7: LGM decreases 2nd number by 3: 3 4 => 3 1. Aryo decreases 1st number by 1: 3 1 => 2 1 => sample test #2
Case 8: LGM decreases 2nd number by 4: 3 4 => 3 0. Aryo decreases 1st number by 3 and wins: 3 0 => 0 0
So BitAryo will win anyway. Is this correct?
LGM in first step decreases both numbers by 2 and wins.
Oh thanks
possible options: 0 4->lose 3 0->lose 1 4->1 2->lose 2 4->2 1->lose 3 1->2 1->lose 3 2->1 2->lose 3 3->lose i.e. only loosing positions are available
I dont know what is trie at all, so I tried to find another solutions, and i found one in comments, here it is: http://codeforces.com/blog/entry/6954#comment-126051
I think problem E's order is O(n log max(a_i)) because when searching on trie, you must visit as many nodes as (a_n)'s digits of binary presentation.
Sorry for the mistake. Fixed.
I have a basic doubt for problem D: we know that for n=2 case 1 2 is a losing position so if for n=3 we have test case like 1 2 3 then 1^2^3=0 implies it to be a losing case for 1st player. but if first player removes 3rd pile completely leaving 1 2 for 2nd player then because 1 2 is losing position 2nd player must loose. So,what will be the soln. for this case.
(1 2) is a losing scenario, because whatever you do, the other player will win in the next turn...
(1 2) -> (1 1) -> (0 0)
(1 2) -> (1 0) -> (0 0)
(1 2) -> (0 1) -> (0 0)
(1 2) -> (0 2) -> (0 0)
But after removing the third pile completely from (1 2 3), you get (1 2 0), which is different from (1 2). (1 2 0) is a winning scenario. The winning move is to remove one from the second pile and leave the other player with (1 1 0). Since there's a 0 involved, the first and second pile can't be removed in the same turn.
Another almost O(1) solution. but for B http://www.codeforces.com/contest/282/submission/3318094
very good editorial. tnx
I don't why people give negative votes for relevant questions. The doubt asked by Persianpars is valid and atleast valid for me because I have the same doubt. If some of you don't think that this is the kind of questions needed to be asked and you know the answer, then please answer it rather than just giving it with negative votes and hiding the commment.
Regarding problem B, it is interesting to observe that a division of labor between A and G satisfying the given property will always be possible; i.e. we will never get '-1' as the answer.
This is because, as the given explanation essentially proves, if assigning G the task of painting the nth egg violates the required condition, then we can be sure that assigning it to A won't.
173B - Chamber of Secrets was very cool it didn't have impossible state
Problem D, my proof and some thoughts :
For N=3 Statement : If we have the numbers A,B,C and A^B^C=0, then (A-P)^(B-P)^(C-P)!=0.
Proof: Let's first say that the length of the binary notation of all our numbers is the same and equals K. (we can accomplish that by adding leading zeroes), now let's look at the K-th bits of our numbers. Obviously if the bitwise XOR results in 0, then we have even numbers of '1's , since N=3, then either 2 of our numbers have K-th bit 1, or none of them. If P's K-th bit is 1, then substracting it from A,B,C will change their K-th bits, so if initially we had even number of ones, we will have odd number of ones, because N is odd, and therefor the last bit of the resulting XOR operation will be 1. So what if P's K-th bit is 0? Then we can simply ignore the last bits and look at the (K-1)th bits, inductively we can prove that all bits of P should be 0, and therefor the only time the statement is wrong is when P=0, which is impossible in our task.
Furthermore i want to explain that this would hold in any odd N, since we will have even number of ones, and similarly we can prove that if some bit of P is 1, then we will have even number of ones at some position and the XOR will not be zero.
For N=2 As mentioned above, known as famous variation of NIM's game, the Wythoff's game has again O(1) solution. According to Wythoff's game theory if the objects in the first pile are A, and in the second B, the N-th losing position is :
A=floor(φ*n)
B=floor(φ*n) + n
or
A=floor(φ*n)
B=floor(φ*φ*n)
because the equation floor(φ*φ*n) = floor(φ*n)+n , holds.
φ — Golden Ratio = (1+sqrt(5))/2
It is interesting if there is O(1) solution for even N>2, if someone knows one, please send it to me. Hope i helped :)
“Using the same DP strategy for n=2 and the O(1) algorithm for n=3 and n=1, leads us to a total complexity of O(n2) which was not necessary in this contest.”
Why DP strategy for n = 2 leads us to a complexity of O(n2)?
my code is O(n3):
for(int i = 0; i <= a[0]; i++) { for(int j = 0; j <= a[1]; j++) { if(win[i][j]) continue; for(int k = 1; k <= 300; k++) { win[i+k][j+k] = 1; win[i][j+k] = 1; win[i+k][j] = 1; } } }Their dynamic idea is quite different, it is explained in the post how to implement it for N=3. They say it leads to O(N^2) if you use O(1) for N=3 and the DP method they use for N=2. If you want to use their dynamic idea for N=2, you do the following:
With [a,b] i will define a position with a being the first number and b the second.
First we define lose[i]=k , where k is the lowest number such that [i,k] is a lose positiong. Now obviously every [i,k+p] , will be a winning position since we can go to position [i,k] in our first move, taking exactly p from the second number and send the second player into a lost position. Also we can notice that [i,k-p] is also always won position since k is the smallest number such that [i,k] is lost, therefor [i,k-p] is win position, otherwise lost[i] would've equaled k-p. Knowing those stuff we understand that for a number i, we have exactly one other number k such that [i,k] is a lost position.
So now how do we fill our lose[] array? Well dynamicly obviously, first obviously lose[0]=0. And then for lose[i], we can iterate from 0 to i-1 and pick such k, so it isn't possible to go from [i,k] to any of the previous ones. For example, computing lose[1], we want such K so we aren't able to go in [0,0], well obviously this is 2, so lose[1]=2 and so on.
Here is a solution i wrote for you to understand what i mean clearer (bad implementation though) : http://codeforces.com/contest/282/submission/3326169
Hope i helped you, sorry for the badly written solution, it's still O(N^2) though :P
I am not able to get how you are saying that if kth bit of P is 1 then kth bit of i-p will flip.?? eg:: i=13 == 1101 , p=7=111 , i-p=6=110.
I'm surprised you found a 4 year old explanation.
Basically, we want to prove that (A-P)^(B-P)^(C-P) is not 0. This means that at least one bit position in the resulting numbers is 1. We start iterating the bits on P from the least significant one. Now suppose that the first non-zero bit of P is at position K.
Well, then when you subtract P from all the numbers, then at position K the values will flip, since all less significant positions are 0 in P (by definition of our choice for K). My original answer explains that for odd N, if you flip some bit position in all numbers then the total number of 1s on that position becomes odd and hence the whole result is non-zero.
Hope you understand that. Feel free to ask questions.
Thanks.I got it.I initially thought you meant most significant bit by kth bit. Now its clear
Yeah, I don't really like my original explanation, but I was 14 back then. It's understandable.
How to solve problem E without trie ? Somebody solved this problem with a multiset and binary search , like this one : http://codeforces.com/contest/282/submission/3309782
This one used a mulset to simulate a trie. It's the same idea as the tutorial , but slower .
ha ha! I got AC for problem D with O(n^4) algorithm! http://paste.ubuntu.com/5706109/
In problem E, can someone tell me why am I getting WA on test case 46?
http://codeforces.com/contest/282/submission/19595312
Sorry to revive this old thread. I cannot understand the proof for problem B. The editorial asserts the following:
Given that it is not possible to add gn to Sg,
From what I understand, this means that if we add an = (1000 - gn) to Sa, then the conditions for the assignment of eggs will be violated. This implies that if it is not possible to assign eggs to G, then it is also not possible to assign eggs to A if we use the greedy strategy mentioned in the editorial.
How does this inequality lead the author to conclude that this inequality " is exactly what we need to make sure that we can add an = (1000 - gn) to Sa"?
abs(Sg-Sa) <= 500 this is required condition.
But what author wants to say is if we can't add Sg + gn then we will be definitely able to add Sa + an This can be concluded from 500 > Sa + (1000 - gn) - Sg
In short, while painting you can choose A or choose G if cant choose one then you will be able to choose another. Hence the solution is always possible and -1 case will never occur. Correct me if I am wrong.
In the Question D can anyone please explain how is the win[i][j][k] is calculated using the lose[i][j] and lose2[i][j],what are their significance.
There is an O(n) solution in D for n = 2. Losing states follow a pattern. (1,2), (3,5), (4,7), (6,11) ... continue. We can prove this, for each number x, there is a pair such that (a, a + x) is a losing state, for all other states we can bring that down to the previous losing state. 85087974
There is an easier solution for B ...
Suppose n = 5 ,
Sa = a1 + a4 + a5 , and Sg = g2 + g3
So , Sa — Sg = a1 + a4 + a5 — (g2 + g3) , Now gi = 1000 — ai (for any i) , so...
Sa — Sg = a1 + a4 + a5 — (1000 — a2 + 1000 — a3) which is , a1 + a2 + a3 + a4 + a5 — 2*(1000)
So , if -500 <= (Sa — Sg) <= 500 for any x such that Sa — Sg = a1 + a2 + ... + an — x*(1000)
Iterate for x from 0 to n , when you find x satisfying the condition , then those are the number of G's and the rest are A's , in any order ...
nice one dude
Can someone suggest me the corner case for my solution for Problem C.
I am getting wrong answer at testcase 49.
This is my code: Link
Regarding problem E, I'd like to ask why a solution using string won't pass the tests (TLE), whereas using dequeue solves the issue. Are operations on strings really that expensive and inefficient?
Here are links to both of my submissions (one getting TLE at 34 and other passing all 101 tests).
https://codeforces.com/contest/282/submission/104195288
https://codeforces.com/contest/282/submission/104196130