Codeforces Round #595 (Div. 3) Editorial

#	User	Rating
1	tourist	3882
2	maroonrk	3539
3	Benq	3513
4	MiracleFaFa	3466
5	ksun48	3462
6	ecnerwala	3446
7	slime	3428
8	Um_nik	3426
9	jiangly	3401
10	greenheadstrange	3393

#	User	Contrib.
1	awoo	192
2	-is-this-fft-	191
3	Monogon	185
4	Um_nik	182
4	YouKn0wWho	182
6	maroonrk	169
7	antontrygubO_o	167
8	errorgorn	166
9	kostka	165
9	SlavicG	165

All ideas belong to MikeMirzayanov.

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int q;
	cin >> q;
	for (int i = 0; i < q; ++i) {
		int n;
		cin >> n;
		vector<int> a(n);
		for (int j = 0; j < n; ++j) {
			cin >> a[j];
		}
		bool ok = true;
		for (int p1 = 0; p1 < n; ++p1) {
			for (int p2 = 0; p2 < p1; ++p2) {
				ok &= abs(a[p1] - a[p2]) != 1;
			}
		}
		cout << 2 - ok << endl;
	}
	
	return 0;
}

1249B1 - Books Exchange (easy version)

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int q;
	cin >> q;
	for (int i = 0; i < q; ++i) {
		int n;
		cin >> n;
		vector<int> p(n);
		for (int j = 0; j < n; ++j) {
			cin >> p[j];
			--p[j];
		}
		for (int j = 0; j < n; ++j) {
			int cnt = 0;
			int k = j;
			do {
				++cnt;
				k = p[k];
			} while (k != j);
			cout << cnt << " ";
		}
		cout << endl;
	}
	
	return 0;
}

1249B2 - Books Exchange (hard version)

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int q;
	cin >> q;
	for (int i = 0; i < q; ++i) {
		int n;
		cin >> n;
		vector<int> p(n);
		for (int j = 0; j < n; ++j) {
			cin >> p[j];
			--p[j];
		}
		vector<int> used(n);
		vector<int> ans(n);
		for (int j = 0; j < n; ++j) {
			if (!used[j]) {
				vector<int> cur;
				while (!used[j]) {
					cur.push_back(j);
					used[j] = true;
					j = p[j];
				}
				for (auto el : cur) ans[el] = cur.size();
			}
		}
		for (int j = 0; j < n; ++j) cout << ans[j] << " ";
		cout << endl;
	}
	
	return 0;
}

1249C1 - Good Numbers (easy version)

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int q;
	cin >> q;
	for (int i = 0; i < q; ++i) {
		int n;
		cin >> n;
		while (true) {
			bool ok = true;
			int cur = n;
			while (cur > 0) {
				if (ok && cur % 3 == 2) ok = false;
				cur /= 3;
			}
			if (ok) break;
			++n;
		}
		cout << n << endl;
	}
	
	return 0;
}

1249C2 - Good Numbers (hard version)

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

const long long INF64 = 1e18;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int q;
	cin >> q;
	for (int i = 0; i < q; ++i) {
		long long n;
		cin >> n;
		vector<int> vals;
		int pos2 = -1;
		while (n > 0) {
			vals.push_back(n % 3);
			if (vals.back() == 2) pos2 = int(vals.size()) - 1;
			n /= 3;
		}
		vals.push_back(0);
		if (pos2 != -1) {
			int pos0 = find(vals.begin() + pos2, vals.end(), 0) - vals.begin();
			vals[pos0] = 1;
			for (int i = pos0 - 1; i >= 0; --i) {
				vals[i] = 0;
			}
		}
		long long ans = 0;
		long long pw = 1;
		for (int i = 0; i < int(vals.size()); ++i) {
			ans += pw * vals[i];
			pw *= 3;
		}
		if (vals.back() == 1) ans = pw / 3;
		cout << ans << endl;
	}
	
	return 0;
}

1249D1 - Too Many Segments (easy version)

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

const int N = 250;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	vector<pair<int, int>> segs(n);
	vector<int> cnt(N);
	for (int i = 0; i < n; ++i) {
		cin >> segs[i].first >> segs[i].second;
		++cnt[segs[i].first];
		--cnt[segs[i].second + 1];
	}
	
	for (int i = 0; i + 1 < N; ++i) {
		cnt[i + 1] += cnt[i];
	}
	
	vector<int> ans(n);
	for (int i = 0; i < N; ++i) {
		while (cnt[i] > k) {
			int pos = -1;
			for (int p = 0; p < n; ++p) {
				if (!ans[p] && (segs[p].first <= i && i <= segs[p].second) && (pos == -1 || segs[p].second > segs[pos].second)) {
					pos = p;
				}
			}
			assert(pos != -1);
			for (int j = segs[pos].first; j <= segs[pos].second; ++j) {
				--cnt[j];
			}
			ans[pos] = 1;
		}
	}
	
	cout << accumulate(ans.begin(), ans.end(), 0) << endl;
	for (int i = 0; i < n; ++i) {
		if (ans[i]) cout << i + 1 << " ";
	}
	cout << endl;
	
	return 0;
}

1249D2 - Too Many Segments (hard version)

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

const int N = 200200;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	vector<pair<int, int>> segs(n);
	vector<int> cnt(N);
	vector<vector<int>> ev(N);
	for (int i = 0; i < n; ++i) {
		cin >> segs[i].first >> segs[i].second;
		++cnt[segs[i].first];
		--cnt[segs[i].second + 1];
		ev[segs[i].first].push_back(i + 1);
		ev[segs[i].second + 1].push_back(-i - 1);
	}
	
	for (int i = 0; i + 1 < N; ++i) {
		cnt[i + 1] += cnt[i];
	}
	
	vector<int> ans(n), sub(N);
	set<pair<int, int>> curSegs;
	int curSub = 0;																																				
	for (int i = 0; i < N; ++i) {
		curSub += sub[i];
		for (auto it : ev[i]) {
			if (it > 0) {
				curSegs.insert(make_pair(segs[it - 1].second, it - 1));
			} else {
				auto iter = curSegs.find(make_pair(segs[-it - 1].second, -it - 1));
				if (iter != curSegs.end()) curSegs.erase(iter);
			}
		}
		while (cnt[i] - curSub > k) {
			assert(!curSegs.empty());
			int pos = curSegs.rbegin()->second;
			curSegs.erase(prev(curSegs.end()));
			++curSub;
			--sub[segs[pos].second + 1];
			ans[pos] = 1;
		}
	}
	
	cout << accumulate(ans.begin(), ans.end(), 0) << endl;
	for (int i = 0; i < n; ++i) {
		if (ans[i]) cout << i + 1 << " ";
	}
	cout << endl;
	
	return 0;
}

1249E - By Elevator or Stairs?

Tutorial

Solution

#include <bits/stdc++.h>

using namespace std;

const int INF = 1e9;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, c;
	cin >> n >> c;
	vector<int> a(n - 1), b(n - 1);
	for (int i = 0; i < n - 1; ++i) {
		cin >> a[i];
	}
	for (int i = 0; i < n - 1; ++i) {
		cin >> b[i];
	}
	vector<vector<int>> dp(n, vector<int>(2, INF));
	dp[0][0] = 0, dp[0][1] = c;
	for (int i = 0; i < n - 1; ++i) {
		dp[i + 1][0] = min(dp[i + 1][0], dp[i][1] + a[i]);
		dp[i + 1][0] = min(dp[i + 1][0], dp[i][0] + a[i]);
		dp[i + 1][1] = min(dp[i + 1][1], dp[i][1] + b[i]);
		dp[i + 1][1] = min(dp[i + 1][1], dp[i][0] + b[i] + c);
	}
	
	for (int i = 0; i < n; ++i) {
		cout << min(dp[i][0], dp[i][1]) << " ";
	}
	cout << endl;
	
	return 0;
}

1249F - Maximum Weight Subset

Thanks to neal for the additional editorial of this problem and providing the linear solution!

Tutorial

Solution (Vovuh, n^3)

#include <bits/stdc++.h>

using namespace std;

const int N = 210;

int n, k;
vector<int> a;
vector<vector<int>> g, dp;

void dfs(int v, int p) {
	dp[v][0] = a[v];
	for (auto to : g[v]) {
		if (to != p) dfs(to, v);
	}
	for (int dep = 0; dep < N; ++dep) {
		if (dep == 0) {
			for (auto to : g[v]) {
				if (to == p) continue;
				dp[v][dep] += dp[to][max(0, k - dep - 1)];
			}
		} else {
			for (auto to : g[v]) {
				if (to == p) continue;
				int cur = dp[to][dep - 1];
				for (auto other : g[v]) {
					if (other == p || other == to) continue;
					cur += dp[other][max(dep - 1, k - dep - 1)];
				}
				dp[v][dep] = max(dp[v][dep], cur);
			}
		}
	}
	for (int dep = N - 1; dep > 0; --dep) {
		dp[v][dep - 1] = max(dp[v][dep - 1], dp[v][dep]);
	}
}

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	cin >> n >> k;
	++k;
	a = vector<int>(n);
	for (int i = 0; i < n; ++i) {
		cin >> a[i];
	}
	g = vector<vector<int>>(n);
	for (int i = 0; i < n - 1; ++i) {
		int x, y;
		cin >> x >> y;
		--x, --y;
		g[x].push_back(y);
		g[y].push_back(x);
	}
	
	dp = vector<vector<int>>(n, vector<int>(N));
	dfs(0, -1);
	cout << dp[0][0] << endl;
	
	return 0;
}

Solution (PikMike, n^2)

#include <bits/stdc++.h>

using namespace std;

#define forn(i, n) for (int i = 0; i < int(n); ++i)

const int N = 200 + 13;
const int INF = 1e9;

int n, k;
int a[N];
vector<int> g[N];
int dp[N][N];
int d[N];
int tmp[N];

void dfs(int v, int p = -1){
	d[v] = 1;
	dp[v][0] = a[v];
	for (auto u : g[v]) if (u != p){
		dfs(u, v);
		int nw = max(d[v], d[u] + 1);
		forn(i, nw)
			tmp[i] = -INF;
		forn(i, d[v]) for (int j = max(0, k - i); j < d[u]; ++j)
			tmp[min(i, j + 1)] = max(tmp[min(i, j + 1)], dp[v][i] + dp[u][j]);
		forn(i, d[u])
			tmp[i + 1] = max(tmp[i + 1], dp[u][i]);
		forn(i, d[v])
			dp[v][i] = max(dp[v][i], tmp[i]);
		for (int i = d[v]; i < nw; ++i)
			dp[v][i] = tmp[i];
		d[v] = nw;
		for (int i = d[v] - 1; i > 0; --i)
			dp[v][i - 1] = max(dp[v][i - 1], dp[v][i]);
	}
}

int main(){
	scanf("%d%d", &n, &k);
	forn(i, n)
		scanf("%d", &a[i]);
	forn(i, n - 1){
		int v, u;
		scanf("%d%d", &v, &u);
		--v, --u;
		g[v].push_back(u);
		g[u].push_back(v);
	}
	dfs(0);
	printf("%d\n", dp[0][0]);
}

include <bits/stdc++.h>

using namespace std; vectorv[100005]; bool vis[100005]; int size=0; void dfs(int n) { vis[n] = true;
size++; for(int x : v[n]) { if(!vis[x]){ dfs(x); }
} } int main() { //int q; //cin>>q; { int n; cin>>n; int arr[n+5],hello[n+5]; for(int i=1;i<=n;++i){ cin>>arr[i]; if(i==arr[i]){ hello[i]=1; vis[i]=true; continue; } v[i].push_back(arr[i]); v[arr[i]].push_back(i); } for(int i=1;i<=n;i++) {
if(!vis[i]){ size=0; dfs(i); //cout<<size<<endl; for(int j=1;j<=n;j++){ if(vis[j]){ hello[j]=size; //cout<<hello[j]<<" "; }

} //cout<<endl; } } for(int e=1;e<=n;e++){ if(e==arr[e]){ hello[e]=1; } cout<<hello[e]<<" "; } }

}

I have for a while commented on the query part for more simplicity.

q = int(input()) for _ in range(q): n = int(input()) Q = list(map(int,input().split())) res=[1]*n for i in range(n): t = Q[i] while t!=i+1: t=Q[t-1] res[i]+=1 print(*res)

#include<bits/stdc++.h> #define ll long long int #define boost ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0); #define mod 1000000007 #define N 200000 #define pii pair<int,int> #define pb push_back using namespace std; vector<pii> s[N+1]; vector<int> e[N+1]; int ec[N+1]; set<pair<pii,int>> st; //<end,size>,num int main() { boost int t=1; //cin>>t; while(t--) { ll n,k; cin>>n>>k; for(int i=1;i<=n;i++) { int l,r; cin>>l>>r; s[l].pb({r,i}); e[r].pb(i); } for(int i=1;i<=N;i++) { sort(s[i].begin(),s[i].end()); } vector<int> ans; int as=0; for(int i=1;i<=N;i++) { for(auto el:s[i]) { st.insert({{el.first,el.first-i},el.second}); } as = st.size(); while(as>k) { assert(!st.empty()); auto it = (--st.end()); ans.pb(it->second); ec[(it->first).first]++; st.erase(it); as--; } for(auto it:st) { if((it.first).first == i) st.erase(it); } } sort(ans.begin(),ans.end()); cout<<ans.size()<<"\n"; for(auto x:ans) cout<<x<<" "; } return 0; }

n = input() int k = 0; // used for counding max power of 3 just greater than n ll int maxp = 1; // as this could overflow in C++ while(tt <= n) { maxp *= 3LL; k++; } // till here maxp = pow(3,k) // k is the max power // here I have tried to use the bitmask approach // I have tried to turn off the ith bit by confirming if it is possible to // make the target value(ans) >= n by turning up all the bits from 0...i-1 // if it is possible then I have turned the bit off (i.e. skipped this power of 3) // else what so ever happens I have to consider this power of 3 in my answer // sum of all 0...i-1 powers of 3 can pe calculated // using GP 3^0 + 3^1 + 3^2 + .... + 3^(i-1) = (3^i - 1)/2 // so if I am on some bit i // then if (ans + (3^i-1)/2) >= n I can skip the power // else ans = ans + 3^i ll int ans = 0; for(int i = k; i > -1; i--){ ll int d = maxp; // using maxp instead of pow(3,i) ll int d1 = d>>1; // same as (pow(3,i) - 1)/2 d1 = d1 + ans; if(d1 < n){ ans = ans + d; } maxp = maxp/3; } output(ans);

import time for q in range(int(input())): n = int(input()) """ Reading I/P in the form of list is not suitable here since we only use p values for look-up. """ # start = time.time() # p_values = list(map(int, input().split())) # # for i in range(n): # pos = p_values[i] - 1 # ans = 1 # while pos != i: # ans += 1 # pos = p_values[pos] - 1 # print(ans, end=' ') # print() # print(f'Time taken by list way {time.time() - start}') """ Reading I/P in the form of Dict makes sense, still getting TimeOut error -_-. And YES!! It makes a significant difference in execution time. Verified by timing it. I/P: 1 6 4 6 2 1 5 3 4 6 2 1 5 3 """ # TODO: NEED TO FIND A WAY TO OPTIMIZE THE EXECUTION. WHAT TO OPTIMIZE?? # start = time.time() p_values1 = {} for i, value in enumerate(input().split()): # Fixing index problem by subtracting p values by 1. p_values1[i] = int(value) - 1 for i in range(n): pos = p_values1[i] ans = 1 while pos != i: ans += 1 pos = p_values1[pos] print(ans, end=' ') print() # print(f'Time taken by dict way {time.time() - start}') # print('END')

Comments (197)

Write comment?

ky4eronline

3 years ago, # |

Thanks for the quick editorial.

→ Reply

Nabil

← Rev. 3 →

-9

[Deleted]

05deepz

i didn't get the output of C1. Can someone make me understand

mhkm

3 years ago, # ^ |

for an input num, if num is good number print it, if it is not, find the next good number and print it.

sh_maestro

For C2, why does a position of 2 in the ternary representation need to be replaced?

upbeat

← Rev. 2 →

What does it mean a position of 2 in the ternary representation? It means that the corresponding power of 3 is used 2 times. But in the problem, it is said that there should not be any power repeated twice or more. That's why the position of 2 in the ternary representation replaced.

Makes sense, I didn't see it that way (different approach to the solution). Thanks for clarifying.

regina-phalange

2 years ago, # ^ |

why cant we replace the 2 in the ternary representation to 1 ? why do we have to replace it with 0 ?

The_Clown_th...

Let's assume we have a ternary representation of 200 (it's decimal equivalent is 2*(3^2)+0*(3^1)+0*(3^0)=18) now if we replace 2 with 1 and replace all 0s to the right of 2 with 1 then we get 111 which is ternary representation of 13. So you see we get a number which is less than 18 but we want a number greater than 18 so we have to set one more bit to 1 to the left of 2 which makes out ternary representation to 1111 (it is decimal equivalent of 40) but now if we make all 1 to 0 except the leftmost 1 then we get 1000 (it's decimal equivalent is 27 ) which is the least number we can get which is a good number and greater than 18. Hope this example will help you to understand the solution better.

Well explained.. Thanks a lot :)

Prajwal_

i am very confused what the turoial want to say,

Naman_Bhalla

+22

For C2, I used a simpler greedy approach. First, I find the smallest number that is the sum of all powers of 3 till the sum becomes >= n. Let us call the sum Z. So this will lead to a number of form 111111 where 1 => The corresponding power of 3 is added to the sum. Now, suppose the highest power of 3 that was included in the sum is m. I go from mth to 0th power and try to subtract corresponding power from current Z. If it leads to a number that is still >= n, we reduce Z by the current power. Else, we continue. Intuition is that if we subtract a larger power, its sum is anyways going to be larger than the sum of all lower powers combined. So it will be a better choice for sure.

My Submission: https://codeforces.com/contest/1249/submission/63202537 (Got AC, I hope no hack :P )

XGptw

i submitted same logic but got wa , i changed the order too.

iamprayush

That's a pretty elegant solution. It does seem quite intuitive, but, do you have any sort of proof of why this greedy approach works?

nonatomicgames

My solution the same. I think we MUST include x=10000 from y=11111 form if n<=y because it's guaranteed that n strictly between 1111 and 11111 (because of previous step, where n>1111) and 10000 smallest option for this 63155044

i saw you code,It was the easiest approach. Thank you so much.

decoder__

21 month(s) ago, # ^ |

Nice Explanantion !! But how do you explain the number will be the closest to the given number?

neal

+51

I have an $$$\mathcal{O}(n \log n)$$$ solution to problem F: 63206899.

The key idea is to merge smaller DP states into bigger. Would have been a nice harder Div. 1 problem. :)

Update: it's actually $$$\mathcal{O}(n)$$$.

+30

It's also funny because I submitted $$$\mathcal{O}(n^4)$$$ in contest: 63153425

qwertyy123321

Can you please explain your approach in detail? thanks.

rsunny

+11

Is it possible for you to provide a quick explanation of your approach ? This looks interesting. I could only come up with O(n2) but O(n) is really impressive.

+26

Since it seems like there's plenty of interest, I wrote a post to explain my full optimization process from $$$\mathcal{O}(n^4)$$$ to $$$\mathcal{O}(n)$$$: https://codeforces.com/blog/entry/70822

Thanks a lot neal :)

INMAK

It was amazing contest!

Spheniscine

+38

sarodesparsh

My thoughts exactly after seeing B. Lmao XD

Hd7

I did the same as you. Despite of the different of implementation, I think the author's ideal is the same, the way he implemented like using dfs :v

Difference is that a simple vector/ArrayList would suffice for finding the cycle, so the image still applies. I don't expect a Div3B problem to require the participants to be familiar with DSU.

Kirito_Rivaille

I use Tarjan to slove problem B2.....

Wow, you definitely win, I don't know Tarjan's lol

It is a algorithm that you can find all the strongly connected components in a directed graph in O(n). Then you can count the size of each strongly connected component.

Subject_Matter1

That's definitely an overkill. I did the same as Spheniscine. Maybe I should look into Tarjan's. That definitely will come in handy.

L_Y_T

Orz wqyzstql,you are so strong !

Thank you very much!

Tarjan is much more overkill =)))

If DSU is a sword, Tarjan's is a chainsaw

But I think DSU is a very common algorithm in some Algorithmic competition...And Tarjan is rarely used.

RetiredDarkMagician

I didn't understand the tutorial of C1 here, more explanation please?

Convert the number to base 3 (ternary). A number is good iff there is no $$$2$$$ digit in it.

For the easy version, incrementing the number until it's good would be sufficient. For the hard version, a more-analytic solution is required.

proJESUS

Why is it that 2 shouldn't be present in the number?

Converting a number $$$n$$$ to base 3 is a way of representing $$$n$$$ as the sum of powers of 3. e.g. if $$$n = 1201_3$$$, $$$n = 1\cdot3^3 + 2\cdot3^2 + 0\cdot3^1 + 1\cdot3^0 = 3^3 + 3^2 + 3^2 + 3^0$$$. The problem requires the powers of 3 be distinct, which means a good number should have no $$$2$$$ in its base-3 representation, as that would mean more than one instance of that power.

temp_1100

why add a power of 3 at pos0 will make remaining element 0 as said in the tutorial of problem c2. I'm not getting it would you please explain it also.

I'd explain it like this:

First, convert $$$n$$$ to base 3, and prepend a leading $$$0$$$. Store this in array $$$s$$$.

Now we want to get rid of all instances of $$$2$$$ in $$$s$$$. How do we do that? Let's just focus on one instance, we'll call its index $$$i$$$.

Now we want to increment $$$n$$$ until $$$s[i]$$$ changes. What happens then? You can imagine $$$s$$$ as being like a car odometer, except in base 3. Thus, the $$$2$$$ will roll up to become a $$$0$$$. When this happens, all digits to the right of $$$s[i]$$$ will be $$$0$$$, and $$$s[i-1]$$$ would increment.

Since getting rid of one $$$2$$$ this way zeros out all digits to its right, we can now fix $$$i$$$ to be the index of the leftmost $$$2$$$.

We're still not done yet though, because if $$$s[i-1] = 1$$$, it's now $$$2$$$, which we don't want. So we zero it out too and continue leftward until we find a $$$0$$$, which is guaranteed because we prepended a leading zero. We can then increment that $$$0$$$ to $$$1$$$, then convert the array back into the final answer $$$m$$$.

thank you so much, i was stuck on this problem for hours.Then i read the turorial still i cant understand it.But you explained so well.Your hardwork is appreciated

rockybalboa01

10 months ago, # ^ |

thanks for such good clarification.

saifulislamsarfaraz

Thanks to your u r

Wow... I really didn't thought it would be a greedy type of problem. Thanks for explaining it tho. Now i see why I couldn't solve it. But I saw one guy used brute force and typed in all the possible value for C1. I was baffled, but he still got it correct.

beerussama

-20

I tried to solve B question both parts using dfs but getting the wrong output due to bug somewhere in the code. could anyone please help me debugging.it would be great help for me.

programmisstt

-6

-_-

jmrh_1

I thought of a greedy for problem D1 which consisted of looking for the segment that had the most points that currently belonged to more than k segments and was updating. Can someone explain to me why this greedy doesn't work.

Wielomian

Look at the testcase

Now you would choose the [10; 20] segment, as it contains 6 points. But then you need to remove 2 more, where you could've deleted segment 4 and 5.

In generał, you can try to disprove greedy by creating example in which the first choice ruins the rest of solution because now you have to pick lots of small elements to solution.

masteranimax

Can you explain why the approach in the editorial is correct

← Rev. 5 →

It's also a greedy approach, but instead we step through the segments in the order of their $$$l$$$, and preferentially remove the segments with the greatest $$$r$$$ when too many cover the current $$$l$$$ value (because removing those segments will lower the count more permanently for future values of $$$l$$$)

See this submission for an example: 63225521

By the way, this problem would be a perfect use-case for a double-ended priority queue (e.g. MinMaxPriorityQueue from the Guava library), but I don't know of any languages that have that in its STL. TreeSet/ordered set works though, with a slightly worse constant factor.

NerfThis

Can you help me understand why my implementation does not work? My submission is 63270199

I did the following: 1. sort all segments first by their r then by l then by index. 2. starting from the minimum to the maximum integer point, do the following. (a).as long as the current segment has not been removed and covers the current integer i, increment the counter cnt for i. (b).if cnt <= k, do nothing, move on to the next integer; else mark all the remaining segments that covers i as removed and increment the deletion counter that needs to be output. If the segment has been removed, do not increment this deletion counter.

I thought this should work as the segments are sorted by their r first. So I am always processing segments that have smaller r. It turns out that I must be wrong somewhere...

I'd appreciate your help.

← Rev. 14 →

You shouldn't sort segments by $$$r$$$ first; you should sort them by $$$l$$$ first, then "sweep" from left to right, maintaining current covering segments in a TreeSet (or a MinMaxPriorityQueue if you're adventurous enough to try implementing one lol). It's the TreeSet/DEPQ that should maintain order by $$$r$$$, because you want to remove the minimum $$$r$$$ entries from the structure that are less than the current $$$l$$$ value (because they aren't covering our "cursor" anymore), as well as preferentially drop the maximum $$$r$$$ entries (and adding them to the answer set) if there are too many segments.

For a TreeSet, a secondary comparator for $$$id$$$ is necessary because TreeSet will assume that entries are equal if the comparator returns 0, and so won't add "duplicates". Since $$$id$$$ is contextually guaranteed to be unique, it's a sufficient tiebreaker.

This "sort by $$$x$$$ first, then put it into a priority queue/set that sorts by $$$y$$$" is actually a very common pattern in CP problems involving segments or time-intervals.

Thank you for your quick reply! I implemented a solution based on your suggestion and it was accepted.

As for the adventurous MinMaxPriorityQueue implementation, now I wouldn't ask you how to solve problem D easier version had I know how to implement that data structure, would I? :)

I am pretty new to competitive programming so it has been quite a struggle here for me in codeforces contests. Mind if I add you as a friend?

Certainly, though the "friend" list on this platform is more like a watch/follow; it doesn't even tell me who added me as a "friend".

I'm glad it helped though! I've been programming for a long time, but it's only recently that I've started to pick up advanced optimization / data structure techniques. I started learning about them while solving the puzzles on http://adventofcode.com , then moved on to here after I've solved them all

Yeah, the UI here is not the best to navigate. There is a send message feature, maybe it is like sending emails?

I've been programming for a few years too but never paid attention to developing my algorithmic skill. Decided to form a habit of solving problems/joining contests to improve my problem solving skill. I first started on LeetCode a few months ago then decided to make it more painful by signing up here. The problems here are definitely a lot challenging.

Yes; "send message" is like private/direct messaging systems on forums

toph3110

12 months ago, # ^ |

Hey , can you help me in D2 of problem of this round?? My approach was to sort by r and then traverse the array and keep a segment tree for counting how many current elements are there in any range. If i can add a segment , I add 1 in range (li to ri) . Then check for next segment if max value between (li+1,ri+1) is less than k , I add it too and keep on doing same . This approach works when k = 1 as it is a standard max activity problem but for larger k it isnt working and I am unable to understand why this doesnot work. Link to my submission

giantPenis

Hi, mate i find jmrh's idea is similar to mine, but not completely the same. i thought that looking for the longest segment that is consisted by more than k points,or the segment consist the points(using the testcase upon, that more than K points would be {10 min,22 max}.)is the most possible one to be pop out,and so on . (first try,it would be seg[10;20],then left with point 21 and point 22 . sec try it would be the seg[21,30] cuz its longest by now and contains 21 and 22,and it's done.)

so is this kind of way could work? how s it compare to the approach in the editorial?

Hi ;) Sorry for late response ;) I don't quite understand, after removal of [10; 20] and [21; 30] point with x = 8 is still present in [1; 9] and [8; 12].

Crap! U got me . Thx bro.i just realized

Np ;) Good luck :)

https://codeforces.com/contest/1249/submission/63210338

I think this is much more arranged than the previous code.

scnucjh

Still don't know why problem F is O(n^3) but not O(n^4)

_trojan_horse

What does dp[u][dep] represent in problem F?

roll_no_1

I think it can be derived like this: Let $$$child_i$$$ denote the number of children of the $$$i$$$-th node.

The total time taken at the $$$i$$$-th node is $$$O(N * (child_i)^2)$$$.

So, the time complexity of the algorithm becomes:

$$$\sum\limits_i (N * (child_i)^2) = N * \sum\limits_i (child_i)^2 \le N * (\sum\limits_i child_i)^2 = N * N^2 = N^3$$$

So, the time complexity is $$$O(N^3)$$$.

MarwanNabil

I think you've forgotten to multiply by the depth , am I wrong :/ ?

so you should write N^4

jnarutoj

20 months ago, # ^ |

The 'N' he's taken is denoting the depth, its not for number of vertices because he's already taken sigma for summation over all vertices.

_sujm

Why this py3 solution for B1 got TLE hacked... I think it is almost same with the tutorial...

grhkm

This is for B1? how does it get hacked :thinking:

yep,63138123,as you can see... Also, I noticed there are many py3 solutions like my submission hacked as well...

I see the hack case now，a simply bad condition which cost 200*200*200 times....sadly for python3,it got TLE. R.I.P

Yea I was just trying py3 the other day and always got TLE. So when I notice how the time execution fluctuates only from a tiny difference of input. I immediately abuse it by giving 200 queries, with 200 numbers and maximum time search.

nikaru_hakamura

I saw some people solved B2 using DFS. Can anyone explain how to solve B2 using DFS?

ritesh1340

For each position ; answer is the size of the connected component in which that element is.

Only those elements are connected which form a cycle.

And size of the connected component can be solved using DFS !

urdarinda

Why doesn't greedy work for problem E? I am thinking, if we use the elevator we continue to use it if we can, If we don't use it, we try to take elevator as much as possible as in next step we won't have to add 'c' if we get the elevator

weapon_x

Maybe $$$b_i$$$ is small but $$$b_{i+1}$$$ is very very large. In that case it is better to pay $$$c$$$ cost and get off the elevator to take the smaller $$$a_{i+1}$$$ cost stairs rather than continue with the elevator. It is better to keep best case scenarios for getting to the floor by both elevator and stairs and keep comparing as you go along.

https://codeforces.com/contest/1249/submission/63192936

What you said is what I wanted to say, meaning we will take the best out of the two but prefer to use elevator if both costs are same

That will be decided by dp, it will factor in the cost of $$$c$$$ against the benefit of $$$a$$$ over $$$b$$$.

Leks360

say u calculate the best cost to reach ith level and to go to (i+1) level u dont always traverse the same path that u did for ith level to reach (i+1)level at ith level say cost is 50 for stair and 60 for elevator and a=100 b=1 c=50 now ur algo will choose 50 as best and try to go to (i+1) by 50+1+50 where as optimally u should choose 60+1

Harshit_90

16 months ago, # ^ |

Test case:

9 3 3 24 17 2 30 27 27 15 1 6 4 7 5 11 22 14

Evil__Coder

Can Anyone Explain why won't we have to check for all previous (1 to i-1) cases for particular i? In this case, it will take O(n**2).

This would be because while travelling from 1 to (i-1), you would have already taken the minimum to reach there. So to reach from (i-1) to (i) , you just need to add the stairs/elevator of the cost from (i-1) to (i) and hence you can ignore all others for particular i

ameya

This is not exactly correct. The DP works because of the structure of the distances, as prefix sums of increasing arrays. In general, you will not be right.

This is because of the structure of the distances to the 1st floor (prefix sums of strictly increasing arrays).

dshahid380

I have submitted two solutions for B1 in Python3 and Pypy3 with the same code. Python3 got TLE but Pypy3 AC. Why there is so much difference between these two? If one logic is accepted in one language then it must be accepted in all available languages given there otherwise giving all languages during submission doesn't make sense. vovuh can you please look into it?

AC solution(Pypy) : 63211941 WA solution(Python) : 63211890

It’s somehow similar to using O3 flag when compiling cpp? I guess it’s just more optimised (most of the time)

Rafaaaaaaaaaaaam

Edited. I read the code again and find that it's not the input()'s fault. Sorry for my last post.

mehulcoder

What if going down was also allowed in E, what difference would it create? How'd we solve it then? Can someone please throw some light on it?

Going down is currently allowed right now, it just won't create an advantage. Because you'll have to go up to the floor, cross it, and then come down, which will always be larger than going up to the floor and stopping right there. So, going down will not give any advantage because of the structure of the problem.

Thanks! Got it now

vovuh

+16

In this problem you are allowed to go down, but this is not optimal at all.

Thanks!

_kite

Anyone else who did B2 with DSU :') ?

kishorerabha

Can you please explain it to me how you did it?

CP_Sucks

Me https://codeforces.com/contest/1249/submission/63148636

gr71

22 months ago, # ^ |

Hey mind explaining the logic ?

shelby

I think my subbmition more easier than in editorail. C1 — C2 Ur opinion https://pastebin.com/xu5nrwzY

ilmaxwell

yeah, nice solution, thx

bl4ckfr05t

For Problem D I created no more than k non-overlapping segments greedily based on shortest right position. This approach seems to fail for some reason, any ideas why it's failing? code

uddeshya.singh

Regarding the C2 question test case 9.

Can someone tell me how can the input of 450283905890997363 expect itself as an answer? the ternary representation of this input is : 10000000000000000000000000000000001200 which has a 2 in it so the correct answer should be 10000000000000000000000000000000010000 convert into decimals, right?

← Rev. 4 →

you are wrong, 450283905890997363 representation of 3^37

upd: you can check diff between 450283905890997363 and 450283905890997444 (your answer) is 81 (fifth bit that equals to 3^4)

You are right, thanks for pointing out 3^37. my conversion function was wrong I guess

In the contest, after long time debug on problem D1 (stupid update error), I even don't read statement E, now I solved it easily without Editorial. I'm very regret about it.

Guaguapi

+13

Here is an $$$O(n^2)$$$ solution for problem F: 63223147 , I used a greedy approach to solve it and have not find any hacks. I think it is a correct approach.

birchtree

Someone also mentioned this in his/her's blog.

https://www.cnblogs.com/wrjlinkkkkkk/p/11726342.html

Oh yeah, thank you !

Can someone explain to me the code for B2?

FLOP

It is obvious that we have bunch of cycles that are not connected.

I keep an array(S) for size of each cycle and an array(N) for each node that shows what cycle they belong to.

for each node i see if it belongs to some cycle . if not i go traverse that until i reach the same node and number all nodes the same(in N) .

like this :


while cur != origin:

    cur = p[cur]

    size_of_cycle ++

so after i checked all nodes for the node i its output is S[N[i]]

pritishn

can someone help me with this?

my failed submission

my accepted submission

the only change in the both is that i commented out

ios_base::sync_with_stdio(false);

cin.tie(NULL);

how does this affect the output?????

I think your vector is out of range , you can test when $$$n$$$ is $$$1e18$$$ ,the variable $$$cnt$$$ is 40 ,but the size of the vector is 39 . Obviously, it is out of range.

GrandDaddy

But I don't understand why removing the fast i/o lines fixes the issue.

I also don't understand. Maybe it's an undefined behavior.

The cnt can't be 40..the input size is max 10^18...so cnt can be max 38

You can debug ,and output the cnt.My complier is visual stutdio ,when n is 1e18,there will be an error that the vector is out of range

Thanks for pointing it out..My last for loop was buggy. Fixing the loop made the solution get accepted without removing ios_base::sync_with_stdio(false)

But i still can't see how removing ios_base::sync_with_stdio also removed the bug XD

I also don't know , we need professionals to answer this strange problem.

juancarlovieri

endl flushes the output

ankyy_0103

In B2, I used set to check if the answer of ith element is already found ,it gave me WA, then i used array to check if element is already answered it got accepted. Doesn't 'contains' method in set in java runs in O(1)?

RandyDKC

why at the end of solution C2 if (vals.back() == 1) ans = pw / 3; ? Can someone help me?

Way_Above_your_level_lol

Take an example and it will be clear to you

why this case is not included in normal cases? I mean the last element changed from 0 to 1 ,exactly after pos2 ,the newly added 0 is pos0.It can also be caculated by the same way above.Why should this case be special?

tanya_sapra

Kindly explain dp[v][dep] in probelm F (Maximum weight subset)?

vaaven

Too good contest, thanks

_Anas__

Another (easier?) implementation of D2

nubir345

19 months ago, # ^ |

Editorialist made D2 implementation way too complicated and for no reason. Here is my submission

rananjay23

Can some one explain Editorial of D2 , i did not got clear understanding .

nilesh8757

If you've understood idea behind D1, then its the same thing done efficiently or say smartly ; observe this code, may be you'll get this from it.

Yeah , i was trying to do without using the set (STL) and that's why i was facing difficulty. I upsolved it finally.

yogi

Can you please explain in detail your approach now @rananjay

rishisharma__

My solution for 1249B2 — Books Exchange (hard version) was giving wrong answer using disjoint set with path compression. Any idea what was wrong ?

rohithill

I am getting WA in D1. Link to solution: https://codeforces.com/contest/1249/submission/63245610

Please help!

alshahreyaj

As usual, I don't understand the editorial.

hetp111

In E. What does it mean by "Time overhead" ? Time to close the door? Time to open the door?

Every time you use the elevator, you need to pay $$$c$$$ in time cost once, in addition to the $$$b$$$ time costs for the floors traveled. (You can imagine it as time spent waiting for the doors to open. Don't think too hard about the real-world logic of it though; this is CP-land) You can ascend several consecutive floors per use, but if you get off to use the stairs, then go back to the elevator, you have to pay $$$c$$$ again.

STommydx

I got another solution for C2 which does not involve any case handling (or dealing with annoying carries!).

We can easily write a function $$$f(i)$$$ that returns the i-th good number. It can be implemented by representing $$$i$$$ in base 2, then treat the resulting digits as a base 3 number. The function runs in $$$O(\log i)$$$.

Then we use binary search to find the smallest $$$i$$$ that satisfy $$$f(i) \geq n$$$. If $$$s$$$ is the smallest $$$i$$$ that satisfy the condition, the answer would be $$$f(s)$$$. The total time complexity would be $$$O(\log^2 n)$$$.

My submission: 63244719

gupta_samarth

Nice approach!

Btw, I think you mean, "express $$$i$$$ in base 2" instead of $$$n$$$. And "$$$f(i)$$$ can be found in $$$O(\log i)$$$".

Thanks for your correction ;)

Single_Ready_To_Mingle

Beautiful :)

diaas

L0u1Za

Is it ok, what a few participants 1600+ rating got it updated after contest?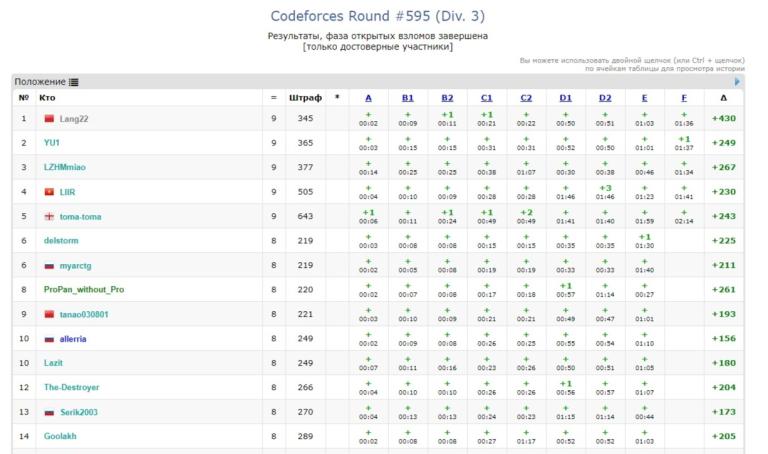

khandelwalnitesh23

PROBLEM -E

https://codeforces.com/contest/1249/submission/63275300

Please tell me what's wrong with my logic. i passed 10 test cases it failed on 11th.

FYI

i am calculating cost from the first floor itself. My logic is i will save the information if i used elevator in the n-1 floor if i am calculating for nth floor(to decide if i have to add 'c' or not ) and i will try to use elevators much as possible.

I had same fail try test case 4 2 4 1 20 2 2 1 but still I have fail in this test.If you solved it pls help

yeeeet

Can problem F be done for general graphs in polynomial time?

BledDest

Nope. Even the case with $$$k = 1$$$ and all $$$a_i = 1$$$ is NP-complete (it is maximum clique problem).

Hiruem

Can anybody explain

ok &= abs(a[p1] — a[p2]) != 1; in problem 1249A

fazeel

In C1 problem why we're using cur%3 == 2?

Line 20: if (ok && cur % 3 == 2) ok = false;

_manvirag

what is the meaning of curSegs.erase(prev(curSegs.end()));

Erasing the last element of curSegs

bladekill

Problem E

Why the jury's answer 14th number is 23 instead of 24? The next number by stairs will have +3 and by elevator either +1 or +3 (1 + 2),

The previous value was 21 so it can be either 24 or 22..

Here is pastebin what I'm talking about: https://pastebin.com/FmZyit6Y.

https://codeforces.com/blog/entry/70779?#comment-556121 see this test case

You are right, the valid output is 0 4 5 7 rather than 0 4 5 8.

kazuya

Hey did you figure out the problem? I have the same doubt.

nagaraj41

I think you didn't use 2 states in your dp, i did the same. Why it will fail is, suppose you can go from the i'th floor to x'th floor by stairs, but you find that, it's optimal to reach the (x+1)th floor by elevator, from the i'th floor. (Note that this is because the cost 'c' is added just once). so obviously you need 2 states of dp for this.

karthik323

in 1249B2 — Books Exchange (hard version) solution . vector<int> used(n) should be of bool type .

C++ doesn't care about the type (int or bool) if you have for example only 1 and 0 values it will treat them like true and false.

vovuh For problem F. The recurrences you mention work if computing the maximum value of a set when distance between any $$$2$$$ vertices is $$$\ge k$$$. But, the problem asks to compute the answer when the distance between any $$$2$$$ vertices is $$$> k$$$. When I read your code, I saw that you are actually incrementing $$$k$$$ beforehand. So, I think you should mention in the tutorial that you change the problem first to the $$$\ge k$$$ version or update the recurrences as:

If $$$dep = 0, dp_{v, 0} = a_v + \sum\limits_{to \in children(v)} dp_{to, k}$$$.
Otherwise, $$$dp_{v, dep} = max(dp_{v, dep}, dp_{to, dep-1} + \sum\limits_{other \in children(v) \setminus \{to\}} dp_{other, max(k-j, j-1)})$$$

Also, there's a typo: "we can notice that this is now what we wanted". I think you meant not.

Yes, I forgot to mention that I increase $$$k$$$ in the beginning of the program to compute the subset with distances $$$\ge k$$$, thank you. And thanks for mentioning the typo, it will be fixed now.

MAHMUD007

what is life

adityaRaj28

please someone help me with the runtime error, the code is running fine on the sample test cases on hackerearth's codetable , but when i am submitting it on codeforces, it is failing for the first test case itself. Test Case: 7 2 11 11 9 11 7 8 8 9 7 8 9 11 7 9

polingram

In C2 tag is given meet in the middle but it is giving TLE . Dd anyone solve this using meet in the middle and binary search , please reply ...

bhasky_06

can someone explain me D1 and D2,i tried to understand but was not able to get it.

rennanrocha

How to optimize this meet in the middle + binary search to C2? 63895945

Yes I am also asking for that

preda2or

by increasing the size of the vector on which binary search is performed, thus reducing the size of the other vector. accepted code : 67982667

MuheshKumar

11 months ago, # ^ |

Can you explain why did you set the value of M(in your code) as 1350851717672992089 instead of some other large number? I tried setting it with a different large number like LLONG_MAX. But the code fails if we set any value other than 1350851717672992089 as a maximum value. I tried including one more power of 3 in the set and ran the same solution with the maximum value being LLONG_MAX, but it got TLE TLE Code. The same code passes AC Code if we remove that extra power of three and set the maximum value to 1350851717672992089. Can anyone explain why this happens?

AmanYdv20

In problem E, why we are not considering the case when the person can go down. For example, if our cost is decreasing after going down and take the elevator or stairs, Why we are not considering that case in the editorial? Any help would be appreciated.

X-O__O-X

What is the shortest path solution for problem E ?

Any accepted shortest path solution for E please ?

What is the Bruteforce approach for C1-Good Number problem?

Abdulrahman98

Problem C1-Good Number.

You can use BitMasks for this problem, since the largest good-number will not exceed 20000 which is equivalent to (3^9).

Minimize the answer to the difference of the sum of the BitMask and x if the condition (sum>=x) is valid.

complexity(9*(2^9))

Can someone explain the recurrence of problem F in detail ?

himanshu_attri

in editorial of C2 why if (vals.back() == 1) ans = pw / 3; we are doing this

tik-tok

2 years ago, # |

Could you please explain the recursive relation in your tutorial of problem F, and what does dep-1 and k-dep-1 mean ? neal

hugcc

Video tutorial of D2: https://www.youtube.com/watch?v=dpOmzwIJkzg

sayan_244

Sorry for hitting this old post.

I wanted to share my thoughts for an alternative solution to E using recursion dp.

For the E elevator and stairs I wrote a recursive approach so initially it struck me that I will end up running my dp solution from top to every other floor which will end up giving a bad complexity of O(N^2).

Well to tackle that we could simply run from the last floor to the top and then we need to take max of the dp values from each floor to the first floor. (Max because along a route with the same minimum time if we go from the top to the floor we take the overhead charges before and as a result we took minimum back then and now starting from that floor on our way to first floor we take overhead charges from that floor already so for the floors where took minimum of the dp values now we have to take maximum instead)

An explanation of also how we could use to move the other way around besides moving from lower floor to higher floor as stated in the problem.

My submission. https://codeforces.com/contest/1249/submission/74881991

P.S- If my solution is incorrect please do let me know. (If it can get hacked)

nimish4july1998

What does that mean

To fix this, let's push dpv,dep to dpv,dep-1 for all depths from n to 1.

MeCoNiKaLoLoLo

This is the (c++ mixed) pseudocode of my code for Problem C.

Nil_paracetamol

23 months ago, # |

at the B2 solution:

if(!used[j])

what does it mean?

shanmukhavarma

a=int(input()) for i in range(a): s=int(input()) s=list(map(int,input().strip(' ').split(' '))) visited={} i=0 length=len(s) while i<length: j=i count=0 while j<len(s): count+=1 j=s[j]-1 if s[j] in visited: print(visited[s[j]],end=' ') break if s[i]==s[j]: visited[s[j]]=count print(visited[s[j]],end=' ') break i+=1 print() i am getting tle pls fix my code for 1249B2

BigSecret

22 months ago, # |

How to solve C2 using meet in the middle?

bever209

21 month(s) ago, # |

Hello I got WA on the test case 1 for the final case, is this because I am only using long?

The last four digits are the only difference. Here is the link https://codeforces.com/contest/1249/submission/90984427.

Thanks

mukund007

19 months ago, # |

idk if anyone's reading this. In the B question can we use "Josephus problem" logic? I tried doing it but couldn't implement it properly. Just wanted to know if it's possible?

DG2701

18 months ago, # |

https://codeforces.com/contest/1249/submission/100273048

why this code is giving wrong answer for B2, Please, can anyone give test case , where it is failing

ArpitGole

17 months ago, # |

Time limit exceeded error when implementing 1249 B1. Books Exchange (easy version) in PYTHON.

I am using a Dictionary for faster searching, still no luck. Please guide me to Optimize my code further.

Thank you.

i_wanna_be_pink

13 months ago, # |

can any one tell what's wrong in my solution to c1 , my idea : to generate all subset (sum it ) and put it in set and check whether it is present or not 114425157

coder_of_india.

13 months ago, # ^ |

115143692 Modified code

thanks man

Welcome!

NinjaSatish

12 months ago, # |

is it me or everyone here is confused with the B questions ...

Ali_Barakat22

9 months ago, # |

i wish if any one can tell me what this line do --p[j]; in the solution of problem B1

JaxYoung

7 months ago, # |

C2's solution can be easier, with just another notice. As this tutorial said before, we can maintain the set of current segments, and we don't only insert its right end point, but also the index of this segment which is unique. So we can make sure we won't erase the same segment twice. So we don't need to consider the $$$curSub$$$, just use the set's size as the number of current segments.

Here's my solution (with some comments): 131618731

cqtshadow

6 months ago, # |

After we calculated all values of dp[v][dep] for the vertex v, we can notice that this is not what we wanted. The current value of dp[v][dep] means the maximum total weight of the subset in the subtree of v if the vertex with the minimum depth we took has depth exactly dep.

I'm very confused about this line, I think that because dp[v][dep] was calculated by the value of dp[v's children][diffdep] (which is the maximum total weight of the subset in the subtree of v's child if the vertex with the minimum depth we took has depth atleast diffdep) so that the dp[v][dep] at that current can't be the maximum total weight of the subset in the subtree of v if the vertex with the minimum depth we took has depth EXACTLY dep.

Maybe I thought it wrong, so can anyone explain to me the logic behind this? Because I believe that only when dep = 0, the statement was correct.

6 months ago, # ^ |

After debugging a lot, I strongly believe that the explanation of the authors about the $$$dp[][]$$$ after calculating (not yet do the push) is wrong.

We can easy to see that because $$$dp_{[v][dep]}$$$ is calculated by $$$dp_{[v's \space child][diffdep]}$$$, and those $$$dp_{[v's \space child][diffdep]}$$$ is given the value about at least depth, not about exactly depth, so we can't guaranteed that $$$dp_{[v][dep]}$$$ after calculated will given the value having exactly depth $$$= dep$$$.

But we still need those push things, it's because the formula didn't consider in all cases, there are cases in which $$$dp_{[v][x]}$$$ will be a better solution than $$$dp_{[v][y]}$$$ $$$(x > y)$$$

For example, with $$$k = 4$$$, the blue node is the root, the yellow means the node we can choose (in the subtree we are considering, and can only choose one of them), the green node is another node that we can also choose after choosing the yellow one (we can choose all or not is depend on the cases), and the red is the un-choose-able node. In this case, we only consider choose node in the subtree of the first child :

It means that the more our dep increase, the more others children node limited will decrease, so yeah, there will be cases that dep bigger is better, so we have to do the push things to make sure the value of $$$dp_{[v][dep]}$$$ is correct.

vovuh's blog

include <bits/stdc++.h>