Articulation Points

Let's define what an articulation point is. We say that a vertex $$$V$$$ in a graph $$$G$$$ with $$$C$$$ connected components is an articulation point if its removal increases the number of connected components of $$$G$$$. In other words, let $$$C'$$$ be the number of connected components after removing vertex $$$V$$$, if $$$C' > C$$$ then $$$V$$$ is an articulation point.

How to find articulation points?

Naive approach O(V * (V + E))

For every vertex V in the graph G do
  Remove V from G
  if the number of connected components increases then V is an articulation point
  Add V back to G

Tarjan's approach O(V + E)

First, we need to know that an ancestor of some node $$$V$$$ is a node $$$A$$$ that was discoverd before $$$V$$$ in a DFS traversal.

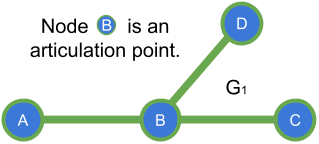
In the graph $$$G_1$$$ shown above, if we start our DFS from A and follow the path to C through B ( A -> B -> C ), then A is an ancestor of B and C in this spanning tree generated from the DFS traversal.

Example of DFS spanning trees of a graph

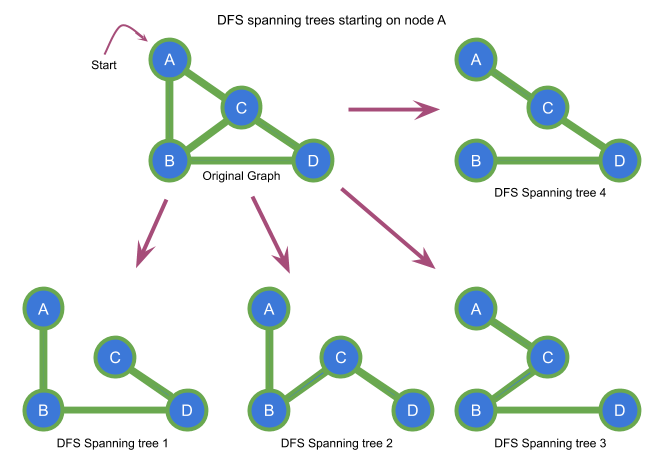
Now that we know the definition of ancestor let's dive into the main idea.

Idea

Let's say there is a node $$$V$$$ in some graph $$$G$$$ that can be reached by a node $$$U$$$ through some intermediate nodes (maybe non intermediate nodes) following some DFS traversal, if $$$V$$$ can also be reached by $$$A$$$ = "ancestor of $$$U$$$" without passing through $$$U$$$ then, $$$U$$$ is NOT an articulation point because it means that if we remove $$$U$$$ from $$$G$$$ we can still reach $$$V$$$ from $$$A$$$, hence, the number of connected components will remain the same.

So, we can conclude that the only 2 conditions for $$$U$$$ to be an articulation point are:

1. If all paths from $$$A$$$ to $$$V$$$ require $$$U$$$ to be in the graph.

2. If $$$U$$$ is the root of the DFS traversal with at least 2 children subgraphs disconnected from each other.

Then we can break condition #1 into 2 subconditions:

• $$$U$$$ is an articulation point if it does not have an adyacent node $$$V$$$ that can reach $$$A$$$ without requiring $$$U$$$ to be in $$$G$$$.

• $$$U$$$ is an articulation point if it is the root of some cycle in the DFS traversal.

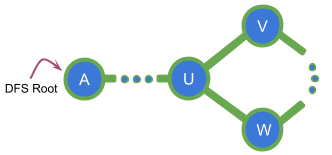
Examples:

Here B is an articulation point because all paths from ancestors of B to C require B to be in the graph.

Here B is NOT an articulation point because there is at least one path from an ancestor of B to C which does not require B.

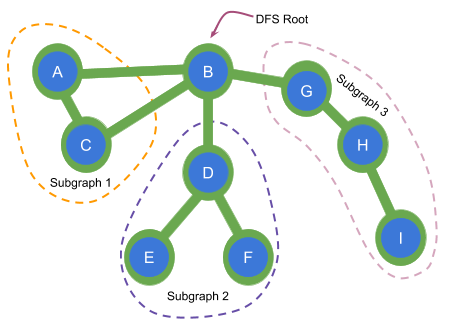
Here B is an articulation point since it has at least 2 children subgraphs disconnected from each other.

Implementation

Well, first thing we need is a way to know if some node $$$A$$$ is ancestor of some other node $$$V$$$, for this we can assign a discovery time to each vertex $$$V$$$ in the graph $$$G$$$ based on the DFS traversal, so that we can know which node was discovered before or after another. e.g. in $$$G_1$$$ with the traversal A -> B -> C the dicovery times for each node will be respectively 1, 2, 3; with this we know that A was discovered before C since discovery_time[A] < discovery_time[C].

Now we need to know if some vertex $$$U$$$ is an articulation point. So, for that we will check the following conditions:

1. If there is NO way to get to a node $$$V$$$ with strictly smaller discovery time than the discovery time of $$$U$$$ following the DFS traversal, then $$$U$$$ is an articulation point. (it has to be strictly because if it is equal it means that $$$U$$$ is the root of a cycle in the DFS traversal which means that $$$U$$$ is still an articulation point).

2. If $$$U$$$ is the root of the DFS tree and it has at least 2 children subgraphs disconnected from each other, then $$$U$$$ is an articulation point.

So, for implementation details, we will think of it as if for every node $$$U$$$ we have to find the node $$$V$$$ with the least discovery time that can be reached from $$$U$$$ following some DFS traversal path which does not require to pass through any already visited nodes, and let's call this node $$$low$$$.

Then, we can know that $$$U$$$ is an articulation point if the following condition is satisfied: discovery_time[U] <= low[V] ( $$$V$$$ in this case represents an adjacent node of $$$U$$$ ). To implement this, in each node $$$V$$$ we will store some identifier of its corresponding node $$$low$$$ found, this identifier will be the corresponding $$$low's$$$ discovery time because it helps us to know when the node $$$low$$$ was discovered, hence it helps us to know by which node we can discover $$$U$$$ first.

C++ Code

// adj[u] = adjacent nodes of u
// ap = AP = articulation points
// p = parent
// disc[u] = discovery time of u
// low[u] = 'low' node of u

int dfsAP(int u, int p) {
  int children = 0;
  low[u] = disc[u] = ++Time;
  for (int& v : adj[u]) {
    if (v == p) continue; // we don't want to go back through the same path.
                          // if we go back is because we found another way back
    if (!disc[v]) { // if V has not been discovered before
      children++;
      dfsAP(v, u); // recursive DFS call
      if (disc[u] <= low[v]) // condition #1
        ap[u] = 1;
      low[u] = min(low[u], low[v]); // low[v] might be an ancestor of u
    } else // if v was already discovered means that we found an ancestor
      low[u] = min(low[u], disc[v]); // finds the ancestor with the least discovery time
  }
  return children;
}

void AP() {
  ap = low = disc = vector<int>(adj.size());
  Time = 0;
  for (int u = 0; u < adj.size(); u++)
    if (!disc[u])
      ap[u] = dfsAP(u, u) > 1; // condition #2
}

Bridges

Let's define what a bridge is. We say that an edge $$$UV$$$ in a graph $$$G$$$ with $$$C$$$ connected components is a bridge if its removal increases the number of connected components of $$$G$$$. In other words, let $$$C'$$$ be number of connected components after removing edge $$$UV$$$, if $$$C' > C$$$ then the edge $$$UV$$$ is a bridge.

The idea an implementation is exactly the same as for articulation points except for one thing, to say that the edge $$$UV$$$ is a bridge, the condition to satisfy is: discovery_time[U] < low[V] instead of discovery_time[U] <= low[V]. Notice that the only change was comparing strictly lesser instead of lesser of equal.

But why is this ?

If discovery_time[U] is equal to low[V] it means that there is a path from $$$V$$$ that goes back to $$$U$$$ ( $$$V$$$ in this case represents an adjacent node of $$$U$$$ ), or in other words we can just say that we found a cycle rooted in $$$U$$$. For articulation points if we remove $$$U$$$ from the graph it will increase the number of connected components, but in the case of bridges if we remove the edge $$$UV$$$ the number of connected components will remain the same. For bridges we need to be sure that the edge $$$UV$$$ is not involved in any cycle. A way to be sure of this is just to check that low[V] is strictly greater than discovery_time[U].

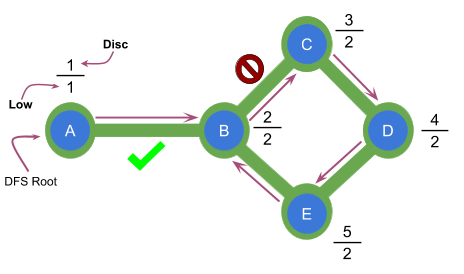
In the graph shown above the edge $$$AB$$$ is a bridge because low[B] is strictly greater than disc[A]. The edge $$$BC$$$ is not a bridge because low[C] is equal to disc[B].

C++ Code

// br = bridges, p = parent

vector<pair<int, int>> br;

int dfsBR(int u, int p) {
  low[u] = disc[u] = ++Time;
  for (int& v : adj[u]) {
    if (v == p) continue; // we don't want to go back through the same path.
                          // if we go back is because we found another way back
    if (!disc[v]) { // if V has not been discovered before
      dfsBR(v, u);  // recursive DFS call
      if (disc[u] < low[v]) // condition to find a bridge
        br.push_back({u, v});
      low[u] = min(low[u], low[v]); // low[v] might be an ancestor of u
    } else // if v was already discovered means that we found an ancestor
      low[u] = min(low[u], disc[v]); // finds the ancestor with the least discovery time
  }
}

void BR() {
  low = disc = vector<int>(adj.size());
  Time = 0;
  for (int u = 0; u < adj.size(); u++)
    if (!disc[u])
      dfsBR(u, u)
}

FAQ

• Why low[u] = min(low[u], disc[v]) instead of low[u] = min(low[u], low[v]) ?

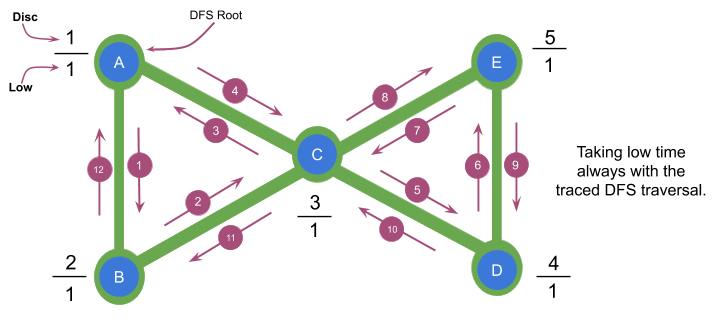
Let's consider node C in the graph above, in the DFS traversal the nodes after C are: D and E, when the DFS traversal reaches E we find C again, if we take its $$$low$$$ time, low[E] will be equal to disc[A] but at this point, when we return back to C in the DFS we will be omitting the fact that $$$U$$$ is the root of a cycle (which makes it an articulation point) and we will be saying that there is a path from E to some ancestor of C (in this case A) which does not require C and such path does not exist in the graph, therefore the algorithm will say that C is NOT an articulation point which is totally false since the only way to reach D and E is passing through C.