The problem: given numbers n and k, find the number of functions 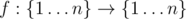 such that for each x with 1 ≤ x ≤ k there is a number r with f[r](x) = 1 and for each x with k < x ≤ n there is no such number r.
such that for each x with 1 ≤ x ≤ k there is a number r with f[r](x) = 1 and for each x with k < x ≤ n there is no such number r.
First, observe that f(x) with x > k can be set to anything in {k + 1... n}, independently to what f is in {1... k}. This means that we can just calculate the number of such functions f restricted to {1, ... k} and multiply by (n - k)n - k by the multiplication principle.
But how do we find how many functions 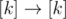 there are that come back to 1 after sufficiently many iterations? If you draw some pictures, you may think about labeled trees: there are k(k - 2) labeled trees on n vertices by [Caley's theorem](http://en.wikipedia.org/wiki/Tree_(graph_theory)#Labeled_trees). Each function corresponds to a unique graph with vertices 1... n and an edge i, j if f(i) = j. The problem statement says that you can come back to 1 if you follow the edges, no matter where you start, this means that there are no directed cycles except the ones containing 1.
there are that come back to 1 after sufficiently many iterations? If you draw some pictures, you may think about labeled trees: there are k(k - 2) labeled trees on n vertices by [Caley's theorem](http://en.wikipedia.org/wiki/Tree_(graph_theory)#Labeled_trees). Each function corresponds to a unique graph with vertices 1... n and an edge i, j if f(i) = j. The problem statement says that you can come back to 1 if you follow the edges, no matter where you start, this means that there are no directed cycles except the ones containing 1.
There is a problem though. Caley's formula counts undirected trees, and we have something that is not even a DAG (because there can be cycles containing 1). We can do a trick to make the thing a DAG — just remove the edge 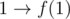 — this breaks the cycle with 1 inside and makes the graph a DAG. Also, it turns out that there are no undirected cycles as well: if there would be an undirected circle, it cannot be a directed one, and this means that some vertex is the cicle has two edges going out from it which is a contradiction because f is a function.
— this breaks the cycle with 1 inside and makes the graph a DAG. Also, it turns out that there are no undirected cycles as well: if there would be an undirected circle, it cannot be a directed one, and this means that some vertex is the cicle has two edges going out from it which is a contradiction because f is a function.
This was a sketch of the proof that the graph is a (unique) labeled tree with an extra edge 
f(1) can have k values, so the answer is: there are k·k(k - 2) ways to choose where the first k values go and (n - k)(n - k) (independent) ways to choose the last n - k. Thus the complete answer is k(k - 1)·(n - k)(n - k).
There are some gaps in the proof: we didn't show that every tree together with the extra edge  corresponds to a function, and that the correspondence is unique.
corresponds to a function, and that the correspondence is unique.










For 1 <= x <= k, I came up with this solution: out of k^k ways we must remove (k-1)*k^(k-1) ways because for each p[i] = i (1 < i <= k) we cannot go back to home 1 from position i. And k^k — (k-1)*k^(k-1) is k^(k-1).
can u tell how u found the formula?