Hi codeforces
Today i will talk about special case in Ternary search
You know when we use Ternary search it's done on a parabola to find its peak
This is a simple code to find the peak of a parabola where the peak is facing down :
L = range_beginning, R = range_ending;
while(R > L) {
x = (L+R)/2;
if( f(x+1) < f(x) )
L = x+1;
else
R = x;
}
But in this special case i need to find the peak of a parabola that has constant value in some ranges as shown on the photo below :
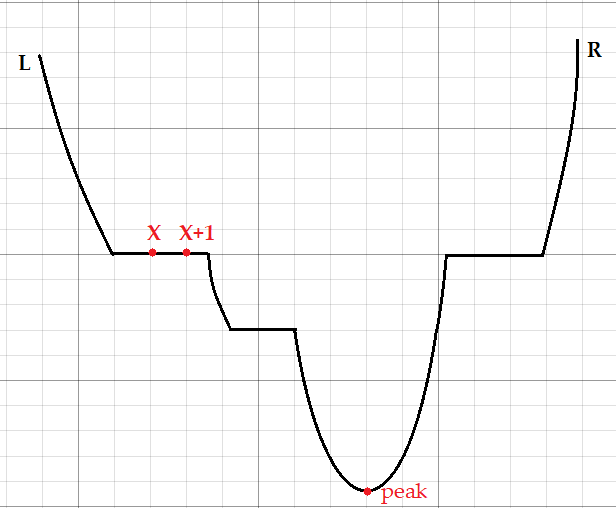
You notice that f(x) = f(x+1) therefor the code from above won't work correctly in this case.
I need help to find a solution for that case.











Auto comment: topic has been updated by Al-Merreikh (previous revision, new revision, compare).
Unless you know something more about this function, this seems quite impossible. Imagine a function that is constant almost everywhere, apart from some tiny interval $$$[l, r]$$$ where it's a convex parabola. For example:
Until you query for a point in that very tiny interval, you won't be able to find the peak (using any algorithm!). If this interval is very small compared to the domain of the function, you'll unfortunately be unable to find the minimum.
Thanks... it's clear to me now.