The inclusion-exclusion principle can be expressed as follows:
To compute the size of a union of multiple sets, it is necessary to sum the sizes of these sets separately, and then subtract the sizes of all pairwise intersections of the sets, then add back the size of the intersections of triples of the sets, subtract the size of quadruples of the sets, and so on, up to the intersection of all sets. The above definition can be expressed mathematically as follows:
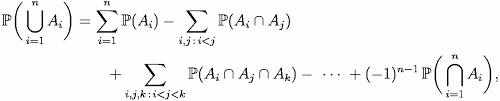
It is intuitive for $$$n\leq 3$$$. But I have some problem with it. I cannot understand why it is like that?! (previously thanks!)










I think you should be able to find an answer in most math textbooks on Combinatorics. Try Googling too. I have a feeling that this question has been answered before countless times as inclusion-exclusion tends to appear in undergraduate courses on counting, probability, etc.
If all-else fails, try asking on Math Stackexchange. I am pretty sure the math geeks there are more than happy to help you out.
https://codeforces.com/blog/entry/64625 does a pretty good job of explaining
there is no rigorous proof
Rigorous proof: use induction. Proof complete!
i tried but didn’t get it, btw thank you:)
Google "inclusion-exclusion principle induction" first answer is a question about exactly that in stackexchange.