300A - Array
In this problem you just need to implement following algorithm. Split input data into 3 vectors: first will contain negative numbers, second positive numbers, third zeroes. If size of first vector is even move one number from it to the third vector. If second vector is empty, then move two numbers from first vector to the second vector. This solution works in O(n).
300B - Coach
Input data represents a graph. If there is a connected component with at least 4 vertexes, then answer is - 1. Every connected component with 3 vertexes is a complete team. Other teams are made from 1 or 2-vertex components. If amount of 2-vertex components is greater than 1-vertex answer is - 1. Otherwise match 2-vertex components with 1-vertex. If there are some 1-vertex components left then split them into groups of three. This algorithm works in O(n + m). Also you could implement O(n4) solution.
300C - Beautiful Numbers
Let's MOD = 1000000007. Let's precalc factorial values modulo MOD. fact[i] = i!%MOD, 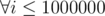 . Let i be an amount of digits equal to a in current excellent number. In this case we can find sum of digits in this number: sum = ai + b(n - i). If sum is good, then add C[n][i] to answer. In this problem it's impossible to calculate binomial coefficients using Pascal's triangle, because of large n. However it can be done this way C[n][i] = fact[n]inv(fact[n - i]fact[i]). inv(a) is multiplicative inverse element(modulo MOD). MOD is a prime number, so inv(a) = aMOD - 2. Calculating this values for each i from 0 to n will give correct answer in O(nlog(MOD)).
. Let i be an amount of digits equal to a in current excellent number. In this case we can find sum of digits in this number: sum = ai + b(n - i). If sum is good, then add C[n][i] to answer. In this problem it's impossible to calculate binomial coefficients using Pascal's triangle, because of large n. However it can be done this way C[n][i] = fact[n]inv(fact[n - i]fact[i]). inv(a) is multiplicative inverse element(modulo MOD). MOD is a prime number, so inv(a) = aMOD - 2. Calculating this values for each i from 0 to n will give correct answer in O(nlog(MOD)).
300D - Painting Square
This picture is helpful for understanding.

Let's consider problem D in graph terms:
We have matrix n × n, which represents a graph:
- It is tree.
- Every vertex, except leaves, has 4 children.
- There are 4k distinct vertexes, with distance k from root.
We need to color k vertexes of this graph. By that we mean also to color all vertexes on path from i to 1(root).
Knowing height of tree we can build it in unique way. Let's find height of tree in this way:
int height = 0;
while (n > 1 && n % 2 == 1) {
n /= 2; height++;
}
Let's consider following DP: z[i][j] — number of ways to color graph height i in j steps.
Naive solution in O(k4log(n)):
z[0][0] = 1; z[0][i] = 0, i > 0; z[i][0] = 1, i > 0
z[i][j] = 0;
for(int k1 = 0; k1 <= j - 1; k1++)
for(int k2 = 0; k2 <= j - 1 - k1; k2++)
for(int k3 = 0; k3 <= j - 1 - k1 - k2; k3++)
{
int k4 = j - 1 - k1 - k2 - k3;
z[i][j] += z[i-1][k1] * z[i-1][k2] * z[i-1][k3] * z[i-1][k4];
z[i][j] %= mod;
}
But it is not what we whant in time terms. Let's consider current DP as polynomial coefficients: z[i][j] — coefficient of power j of polynomial i. In that case z[i + 1][j + 1] — coefficient of power j of polynomial i to the 4-th power. This approach allows to solve problem in O(k2log(n)). However this solution is quite slow, because of modulo operations. As you see, this modulo is not so big ( ≤ 107), that allows us to reduce number of modulo operations, thus giving huge perfomance boost. Also it is possible to use FFT to solve in O(klog(k)log(n)).
Аuthor's solution. Without FFT
300E - Empire Strikes Back
Let's 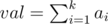 . val is upper bound for answer. val! is divisible by
. val is upper bound for answer. val! is divisible by 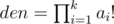 , you can easily prove it using facts about prime powers in factorial and following inequality
, you can easily prove it using facts about prime powers in factorial and following inequality 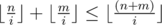 . By the way,
. By the way, 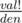 is called multinomial coefficient. So answer can't exceed 1013.
is called multinomial coefficient. So answer can't exceed 1013.
If n! divisible by den, then (n + 1)! is also divisible by den. That means that function of divisibility is monotonic and we can use binary search.
For every i, i = 2..., 107, let's precalc max prime in i using linear sieve of Eratosthenes. For i it will be lp[i]. After that let's create a vector, with all primes less then 107.
Now let's calculate following values cnt[i] — amount of numbers a, i < = a.
Now me can factorize denominator like this:
for(int i = max; i>=2; i--) {
if (lp[i] != i)
cnt[lp[i]] += cnt[i];
cnt[i / lp[i]] += cnt[i];
}
Finally we use binary search from lf = 1 to 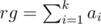 .
.











What is O(n^4) solution for B?
I used Floyd-Warshall which works in O(n^3).
Authors solution for E looks to be a different program from the intended.
thanks. Now fixed.
I think by mistake both are same link in D
Thank you.
Really great to have the analysis so quickly, btw!
About solution C, I will appreciate a theory reference for the MOD-2 theorem in the inverse! Thanks
You can read it here, for example. It's based on Euler's theorem.
For solution D, can you (or someone) explain what are the following pieces of code doing?
It's basically splitting power of 4 into two square operations. The first calculates power of 2 on the polynomial, stored into a temporary array, then the second calculated power of 2 on the temporary array.
Thanks! but I don't really understand this too:
Let's consider current DP as polynomial coefficients: z[i][j] — coefficient of power j of polynomial i. In that case z[i + 1][j + 1] — coefficient of power j of polynomial i to the 4-th power.
what does that mean by "to the 4-th power" and why is that the answer?
Is it just me or is E actually easier than D? (I used an approach different to the max-prime, instead I used a modified sieve of Erathostenes to determine the exponent of each prime in the product by looping through all the integers divisible by it and getting max. powers of this prime dividing each of them.) Almost did it during the contest, too... or maybe I just like number theory :D
can anybody clarify the naive solution of D ? I cant understand it although read again and again..
firstly,we can calc how many times can we divid the square,if two square have the same times of divding,their answers is the same,so we just care about how many times the square can be divided. secondly,we can find the**_ subproblem_** of this problem , if we divide a square into four parts,and we can assigned every part a number(dividing times)__ , for example :a b c d. it means part1 be divided a times , part2 be divided b times ..and so on. we'd better construct the square from small to big. So the dp state is dp[i][j] :the tot number of ways when we are constructing the ith small square , we have draw j times , every step ,the square just become two times bigger. the transion is simple , just enumerate the four parts's draw times respectively , and we got a two size bigger square,when doing transion ,we must use a little optimizatioin see my code here
thanks a lot! you write clearly i understand now :)
Man, you are the real MVP
for Problem E,I've seen this code ,but I can't understand what does the following code try to do
anyone help me ? thanks a lot
Delta[i] is the number of times that i is being multiplied in the denominator, that is, the number of x's such that a[x] >= i. It is calculated in such a way that if you get the sum of Delta[i] * i for all i, that sum would be the denominator.
Min[i] is the index of the minimum prime number that divides i.
Count[i] is the number of times that the denominator can be divided by the ith prime. So what he does in that for is really factoring the denominator in prime factors in an efficient way. Another way of doing it is: for each i, for each prime factor x of i, count[indexOfPrime[x]] += Delta[i] * timesDivide(i, x). But this way is less efficient.
An example: suppose i is the the number (2^3) * (3^4) = 648 and that 648 is 5 times in the denominator (for example if the denominator is 1000! * 648! * 649! * 700! * 701!), then you would add to count[indexOfPrime[2]] the value 5 * 3 and to count[indexOfPrime[3]] the value 5 * 4.
At the end the denominator is factored in this way denominator = 2 ^count[0] + 3 ^ count[1] + 5 ^ count[2] + 7 ^ count[3] + ... + i ^ count[indexOfPrime[i]] and you can continue with the binary search.
As a guy with limited programming experience and weak maths, the tutorial for E was a little over the head for me.. Can someone please explain the solution in a better way with each step elaborated properly..??? thanks in advance..
It's hard for me to explain ,but anyway , I will try. First'y we should get lp[i] as the editorial says. and then we should use lp[i] to split all the numbers
cnt[i] is the times prime factor i appear , initially cnt[i] is the numbers bigger than i , so cnt[lp[i]] += cnt[i] and cnt[lp[lp[i]]] += cnt[i].. and so on. but the way of the code above is faster and clever .
How to proof the problem C's solution: "MOD is a prime number, so inv(a) = a^(MOD - 2)"?
Fermat's little theorem. We know that a^(MOD-1)=1 modulo MOD. By definition, inv(a)=a^(-1) and multiplying by a^(MOD-2) gives inv(a)=a^(MOD-2). (The equalities are in fact congruences.)
Note that this is only valid for coprime a and MOD.
Have a look at this article too...
http://en.wikipedia.org/wiki/Euler's_theorem
the fermat's theorem is a case of euler's theorem, with the totient function being equal to (p-1), where p is prime.. i hope it satisfies u...
Thank you very much!
In the author's solution of problem D what is the significance of the value of root_1?
I know it's very late but I would really appreciate if someone could help me with understanding this statement regarding problem D-
"Let's consider current DP as polynomial coefficients: z[i][j] — coefficient of power j of polynomial i. In that case z[i + 1][j + 1] — coefficient of power j of polynomial i to the 4-th power. "
What is the meaning of 'coefficient of power j of polynomial i'? What does one mean by 'polynomial i'?
gridnevvvit can u please share the image related to problem D or explain what is there in the image as I am not able to view it? I also tried going to the url of the image but had no success. Thanks in advance.
Also in problem D, how do you model n * n matrix as a graph (tree) with each node having 4 children? What is the root of the tree?
Why permutations with repetitions doesn't solve problem C?
you can solve with permutations, but its a different type of permutation, see this link
I used DSU to solve problem B with $$$O(n^2log(n))$$$. Mine
Hello Everyone!!
I was solving the C problem of this contest and getting "Time Limit Exceeded". I don't know where to optimize further. I also looked at the author's solution and I guess it is pretty much the same. It would be great if someone could walk me out of this problem.
The link to my solution is: 74799789
TIA
Ignore this comment. I found my mistake :)
No. I've checked all the TCs now and they are all <=1e6. Can you tell which TC exactly crosses this limit?
O(N) solution for problem C 98275817