305A - Strange Addition
All you have to do is implement following algorithm:
- If we have numbers 0 or 100, we take them to needed subset.
- If we got number greater than 0 and less than 10, we take it.
- If we got number
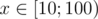 divisible by 10 we take it.
divisible by 10 we take it. - In case we have no numbers of second and third type, we take a number
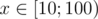 that is not divisible by 10
that is not divisible by 10
305B - Continued Fractions
There are at most two ways to represent rational fraction as continued. Using Euclid algorithm you can do that for  and then check equality of corresponding ai.
and then check equality of corresponding ai.
305C - Ivan and Powers of Two
First of all, let's carry over all powers of two in the following way: if we have ai = aj, i ≠ j, carry 1 to ai + 1. Now as all of ai are distinct, the answer is max(ai) — cnt(ai) + 1, where max(ai) — maximal value of ai,cnt(ai) — size of a
305D - Olya and Graph
First of all let's consider a graph on a number line. It's neccesary to have edges i - > i + 1(first type). Also you can edges like i - > i + k + 1 (second type). Other edges are forbidden. This allows us to understand whether the answer is 0 or not. Also answer is 0 when all edges of second type doesn't intersect, considering them to be segments of number line, except when k ≥ n - 1 — in this case answer is 1. Now we know that answer != 0. Frow all edges we have let's use only second type edges. If there aren't any of this edges we can add 1 to the answer, because of possibility of adding 0 edges to graph. For every vertex i, that has possibility of adding second type edges, let's add to answer 2cnt, cnt — amount of vertexes on [i, min(i + k, n — k — 1)] without edges of second type out of them. Also it is necessary for all the second type edges to start in this segment.
Solution O(n + m) Solution O(m + log(n))
305E - Playing with String
Let's consider substring of s s[i... j], that all characters from i to j are palindrome centers, and i - 1, j + 1 are not. Every such substring can be treated independently from the others, and as we don't need to know it'sstructure let's consider only it length len. Let's calculate grundy[len] — Grundy function. If we want to cut character at position i 0 ≤ i < len then our game splits in to independent ones: first will have length i - 1, second — len - i - 2, as s[i - 1] and s[i + 1] are not centers of palindrome any more.











The sample (case #5)"2 1 2"on A — Strange Addition, the answer is "1 1".I want to know how to choose two distinct numbers in the set. Because of it, I failed the previous test.
I failed on pretest 5, the answer has only 1 number. I think the explanation is "if there is only one number in the set, you cannot find two numbers which don't meet the requirement, since 1 > 0, you should choose that number".
You means the pretest #5 is right?
Yes, answer contains at least one number, because it's always better than 0 number.
If there are only one number in set -> we cannot choose two distinct numbers, so for all (0) pairs conditions holds.
It is still hard to persuade me. Anyway, thank you for preparing the context.
Wrong name for 305E in the editorial.
Fixed
I am a bit confused about Div2 — P1 Why should I take all numbers x, (1 <= x <= 9)?
Not all, only one
Now I am having doubt that I even understood the problem statement. :(
What does it actually require?
What I thought was that, I need to pick the largest subset such that for any two elements, a & b, one would have a 0 in its decimal place.
Seems like I got it all wrong...
Statement says: Vasya can only sum pairs of integers (a, b), such that for any decimal place at least one number has digit 0 in this place. So, for example, we cannot sum 10 and 20, because 10 and 20 has digits 1 and 2 at first decimal place.
You should pick the largest subset that for every two elements, a and b, there should be at least one zero in a%10 and b%10, at least one zero in a/10%10 and b/10%10, and at least one zero in a/100%10 and b/100%10.
I think this solution is much easier.
For C, how can one prove that the above relation would yield us the most optimal answer?