Update 1 Added links to my code.
Update 2 The links to my code seems not work, so I push my codes on github, and you find all of them here: https://github.com/cgy4ever/cf190
Update 3 Fixed my solution of Div1-C (Div2-E). In this problem, we must find centroid of tree instead of center of tree. Thanks RomaWhite for pointing this out and provide test case. And it seems that many solutions can pass the system test will fail on his test case (including my model solution). I feel apologetic for the weak test cases and wrong solution.
Update 4 Reformat the passage, I hope it would looks better.
Let's define remainNew = # of people haven't danced before. So at beginning remainNew = n+m, and we have:
- During the 1st song, remainNew must decreased by at least 2. (Because the boy and girl must haven't danced before.)
- During the k-th (k>1) song, remainNew must decreased by at least 1. (Because one of the boy or girl must haven't danced before.) So the answer must be no more than n+m-1.
And it's not hard to construct one schedule get this maximal possible answer:
1 1
1 2
...
1 m
2 1
3 1
...
n 1
If there are no "mixing bouquet" then the answer will be r/3 + g/3 + b/3. One important observation is that: There always exist an optimal solution with less than 3 mixing bouquet.
The proof is here: Once we get 3 mixing bouquet, we can change it to (1 red bouquet + 1 green bouquet + 1 blue bouquet)
So we can try 0, 1, 2 mixing bouquet and make the remain 3 kind of bouquets use above greedy method. Output one with largest outcome.
322C - Ciel and Robot 321A - Ciel and Robot
Note that after Ciel execute string s, it will moves (dx, dy). And for each repeat, it will alway moves (dx, dy). So the total movement will be k * (dx, dy) + (dx[p], dy[p]) which (dx[p], dy[p]) denotes the movement after execute first p characters. We can enumerate p since (0 <= p < |s| <= 100), and check if there are such k exists.
Note that there are some tricks:
- We can divide dx or dy directly because they both can become zero.
- Another trick is that k must be non-negative.
Many people failed on this test case (which no included in the pretest):
-1 -1
UR
322D - Ciel and Duel 321B - Ciel and Duel
We have 3 solutions to this problem:
= 1. greedy =
There are 2 cases: we killed all Jiro's cards, or not.
If we are not killed all of Jiro's cards, then:
-
- We never attack his DEF cards, it's meaningless.
- Suppose we make k attacks, then it must be: use Ciel's k cards with highest strength to attack Jiro's k cards with lowest strength, and we can sort the both k cards by strength to make attack one by one. (If there are an invalid attack, then we can't have k attack)
If we kill all Jiro's card: Then for all DEF cards, we consider it from lower strength to higher: if its strength is L, then we find a card of Ciel with strength more than L (If there are many, we choose one with lowest strength). Then we can know if we can kill all DEF cards. And then we choose |x| cards with highest strength of Ciel, try to kill Jiro's remain card.
Note that if we could kill all ATK cards, the order doesn't matter: the total damage will be (sum of strength of Ciel's remain card) — (sum of strength of Jiro's remain card).
= 2. DP =
Above solution looks complicated, can we solve it with few observation? Yes we can. The only observation is that:
There always exist an optimal solution that: If Ciel's two card X's strength > Y's strength, and X, Y attacks on A and B with the same position, then A's strength > B's strength. We already use this observation in above solution.
Then what can we do? Yes, we can sort all Ciel's card, all ATK card of Jiro, all DEF card of Jiro.
Let's DP[pCiel][pATK][pJiro][killAll] be the state that next unconsidered card of Ciel, Jiro's ATk, Jiro's DEF are pCiel, pATK, pJiro, and killAll=1 if and only if we assume at the end we can kill all Jiro's card.
Then we have 4 choice:
- Skip, this card don't attack.
- Attack on the next ATK card.
- Attack on the next DEF card.
- Assume Jiro has no cards and make a direct attack.
= 3. MinCostMaxFlow =
Well, what if we want to solve this problem with no observation?
Ok, if you are good at construct flow algorithm, it's an easy thing to solve this by flow.
Please see my solution for details. It just considered the matching relationship.
322E - Ciel the Commander 321C - Ciel the Commander
This is a problem with construction on trees. And for these kind of problems, we usually use two method: up-down or down-up. So we have 1 solution for each method:
= 1. up-down construction =
Suppose we assign an officer with rank A at node x. Then for two distinct subtree rooted by x, says T1 and T2: There can't be any invalid path cross T1 and T2, because it is blocked by node x. (It's clear that we can't make 2 rank A officer.)
So we can solve these subtree independently: the only different is that we can't use rank A anymore.
Then the question is: which node should x be? It could be good if any subtree will has a small size. And if you have the knowledge of "centroid of tree", then you can quickly find that if x be the centroid of this tree, the subtree's size will be no more than half of the original tree. So we only needs about log2(n) nodes and 26 is enough.
= 2. down-up construction =
The above solution involves the concept of "centroid of tree" but you might not heard about that, don't worry, we have another solution can solve this problem without knowing that, and it's easier to implement.
Suppose we choose 1 as the root and consider it as a directed tree, and on some day we have the following problem:
We have some subtree rooted at T1, T2, ..., Tk, and they are already assigned an officer, we need to assign an officer to node x and link them to this node. Well, a normal idea is: we choose one with lowest possible rank.
The rank of x should satisfy:
- If there are a node with rank t exposes at Ti and a node with t exposes at Tj (i!=j), then rank of x must be higher than t. (Otherwise the path between them will be invalid.)
- If there are a node with rank t exposes at Ti, then the rank of x can't be t.
So we can use this rule to choose the lowest possible rank. But can it passes? Yes, it can, but the proof is not such easy, I'll introduce the main idea here:
- We assign each node a potential: p(x) = {2^('Z' — w) | w is exposed}. For example, if 'Y' and 'Z' are exposed, then p(x) = 1 + 2 = 3.
- We can proof p(x) <= |# of nodes of the subtree rooted by x| by proof this lemma: When we synthesis x with T1, T2, ..., Tk, p(x) <= 1 + p(T1) + ... + p(Tk). It's not hard to proof, but might have some cases to deal with.
For this problem we need a big "observation": what setup of "flips" are valid? What means set up of "flips", well, for example, after the 1st step operation of example 1, we get:
1 1 0
1 1 0
0 0 0
It means the left top 2x2 cells are negatived.
Given a 0-1 matrix of a set up of "flips", how can you determine if we can get it by some N x N (I use N instead of x here, it don't make sense to write something like x x x.) flips.
To solve this problem, we need the following observation:
- For any i, any j<=x: setUp[i][j]^setUp[i][x]^setUp[i][j+x] will be 0.
- For any i, any j<=x: setUp[j][i]^setUp[x][i]^setUp[j+x][i] will be 0.
It's quite easy to proof than find that: after each operation, there always be 0 or 2 cells lay in {setUp[i][j], setUp[i][x], setUp[i][j+x]} or {setUp[j][i], setUp[x][i], setUp[j+x][i]}.
So what? Well, then there must be no more than 2^(N*N) solutions, since if we determine the left top N x N cells, we can determine others by above equations.
And then? Magically we can proof if one set up meets all above equations, we can get it. And the proof only needs one line: think the operation as addition of vectors in GF2, then we have N*N independent vector, so there must be 2^(N*N) different setups we can get. (Yes, I admit it need some knowledge, or feeling in linear algebra)
Then the things are easy: we enumerate {setUp[1][N], setUp[2][N], ..., setUp[N][N]}, and determine others by greedy. (More detailed, by columns.)
You can find details in my code.
This problem may jog your memory of OI times (if you have been an OIer and now grows up, like me). Maybe some Chinese contestants might think this problem doesn't worth 2500, but DP optimization is an advanced topic in programming contest for many regions. It's quite easy to find an O(N^2 K) DP:
- dp[i][j] = max{ k | dp[i-1][k] + cost(k+1...j)}
(dp[i][j] means the minimal cost if we divide 1...j foxes into i groups)
There are many ways to optimize this kind of dp equation, but a large part of them based one the property of cost function. So we need to find some property independent of cost function.
Let opt[i][j] = the smallest k such that dp[i][j] = dp[i][k] + cost(k+1...j) Then intuitively we have opt[i][1] <= opt[i][2] <= ... <= opt[i][n]. (I admit some people don't think it's intuitively correct, but it can proof by some high school algebra)
Then how to use this stuff?
Let n = 200 and suppose we already get dp[i][j] for i<=3 and now we have to compute dp[4][j]: If we first compute dp[4][100], then we can have opt[4][100] at the same time.
And when we compute dp[4][1] ... dp[4][99], we know that the k must lay in 1...opt[4][100]. When we compute dp[4][101] ... dp[4][200], we know that k must lay in opt[4][100]...n.
Let's formalize this thing: We use compute(d, L, R, optL, optR) to denote we are computing dp[d][L...R], and we know the k must be in range optL...optR.
Then we have:
compute(d, L, R, optL, optR) =
1. special case: L==R.
2. let M = (L+R) / 2, we solve dp[d][M] as well as opt[d][M]. Uses about (optR-optL+1) operations.
3. compute(d, L, M-1, optL, opt[d][M])
4. compute(d, M+1, R, opt[d][M], optR)
One can show that this solution will run in O(NlogN * K). Note that we don't need opt[d][M] at the center of interval optL...optR. We can proof at each recursive depth, the total cost by line 2 will be no more than 2n. And there are at most O(log(n)) depths.










WOW, very fast editorial. Thanks for it
Thanks for the fast editorial! ;)
In "322A — Ciel and Dancing", you wrote:
...
1 m
2 1
2 1
...
I think you have repeated "2 1". The second one should be "3 1".
Yes, you are right. Fixed. Thanks for finding that!
ThanQ! It was so fast, I think system testing will be as fast as Editorial!
Thanks for writing the editorial and preparing a great contest. Hope you add the links to your submissions (e.g. "Please see my solution for details.").
Yes I'll submit the solution after system testing. :)
For 2, I'm sure it's "there can't be any invalid path that spans over T1 and T2". Because all paths will pass that officer with rank A, so all paths will be valid (either different ranks or equal ranks that is monitored by A).
(Point addressed is edited out.)
Oh, I misunderstood the problem, A being ranked greater than B. I though A being ranked less than B.
I WA so many time.... this contest taught me a lot.....Thank you for this contest~
Because the pretest is so weak and the system test is so strong...there are so many WA in the status during the system test....As a result...the system test is so fast....just half an hour...What amazing!
U NO KNOV ENGRISH?
and u ?
Ciel and Duel: Assignment problem (Hungarian algorithm)??? I tried it but failed on test 28.
I guess assignment problem is never necessary to solve Div 2. There must always be some other solution, usually easier.
Links to code not working yet :(
Yes I see. It seems that I'm super user to this contest and my submission can't be viewed by others. I'll post them on other site instead.
It seems that author solution for problem C is incorrect. It fails on test case generated by following code. http://pastebin.com/e6HjC7Aw
Yeah. This is my generator. :)
http://pastebin.com/gFtNHkeG
We must find another "center of tree", not a middle of diameter of tree.
For any tree there is a vertex whose subtrees have a sizes not more than a half of number vertices in original tree. We can find it in the following way:
Assign any vertex to current.
If current satisfies to condition, we find it.
Otherwise there is only one huge subtree. Assign root of this huge subtree to current and go to step 2.
It's easy to prove correctness of this algorithm.
I do this in a different way.
First, find all leafs of the subtree for which you want to find the center. Can be done using BFS starting from arbitrary vertex of the subtree.
Now, traverse the tree upwards in a BFS from the leafs, adding a parent of the vertex viewed at any moment only if it's the last son viewed in the BFS. This equals to partitioning the tree to layers starting from the leafs, and therefore works.
The last vertex viewed by this BFS is the center (or one possible center) :D
I really like this way.
As it was said, you must find "another center of the tree". Your approach finds typical center, so it also fails on this test.
It works in linear time from the number of vertices of the subtree. So, you can just do it again when you need to find another center of a subtree. Mind that I said that we're starting from any vertex of the subtree (for which we want to find the center).
My implementation (AC during contest) is here: 3984297. As you can see, I delete the center and calculate new centers for the subtrees formed. Run your tests on that and then tell me it fails.
Yes, it fails. Many AC solutions fails on this test.
Yes, you are right. My solution was incorrect.
Fortunately it didn't affect the jury, because the checker don't need the output from my solution.
Unfortunately jury has a weak testset for this problem. It isn't a very serious jury's fail, but it's a fact.
P.S. Thanks for the contest :)
In problem Ciel and Gondolas, If we use what opt[i-1][j] <= opt[i][j] <= opt[i][j+1] and calc dp in i=1..k, j=n..1, d=opt[i-1][j]..opt[i][j+1] our solution will be NK ?
Can you explain why opt[i-1][j] <= opt[i][j] <= opt[i][j+1]? Thanks!
Ultra cool idea on E, really like author solution :) But I've got an AC just setting opt[i][j] := opt[i][j-1], and then repeat searching for better move in range opt[i][j] .. opt[i][j] + 100. And in my solution opt was the biggest K such as ..
Where can i get information about finding "Center of Tree"?
See below. There are two algorithms for finding different "centers of tree".
div1 problem E,does the solution above really work?I got TLE test14...
Change
to
thx! I thought 'scanf' is the fastest input,so strange...
The best optimization while using cin and cout for this problem is to input the matrix u's entries as characters and not integers.
TLE using integer input: 49754923
AC using char input: 49754933
Yes, that worked thanks
In Div1E, what does cost(k+1...j) mean?
sum of the value of people from number k+1 to number j
thx!
So is the solution for 322E — Ciel the Commander correct ?
yes
Hi, I've tried to solve your problem 321C - Ciel the Commander. I use a diffrent solution for this problem but I got WA in test case #5. I found my ans is also right in that case. If you have time, may you have a look? My submission ID is 4054120 Upd: Sorry, I've already find my problem.
I always use binary search to solve the DP whose options are monotonic.But now I know a more simple approach for coding that is divide and conquer!Thanks a lot.
in Div1 E why opt[i][1] <= opt[i][2] <= ... <= opt[i][n] is always true ?
I couldn't prove it
Think of the cost function as a matrix C. The problem required is exactly finding diagonal blocks (squares in the matrix that are non intersecting and contain the diagonal on it's union, search for block-diagonal matrices and it may help to understand) of minimal sum this helps on devising a clear proof of the property. I wrote this on a rush, if it didn't help answer this and I may write a careful proof. Good luck.
Assume BWOC that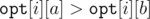 where a < b.
where a < b.
For brevity let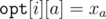 , and
, and 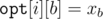 .
.
Then we have by assumption: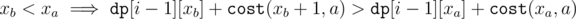
Opening the summation: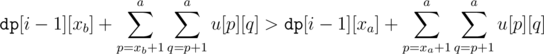
which is a contradiction.
-
This is how I proved it:
Let kj be the optimal point for dp[i][j] and kj - 1 be the optimal point for dp[i][j - 1] where dp[i][j] is defined as the min. total unfamiliarity while distributing first j people in first i gondolas.
Now, we know there is some optimal point for j people and i gondolas namely kj. This means that in the optimal case we'll be left with kj people which then will have to be distributed in (i - 1) gondolas. Now consider having same no. of gondolas but (j - 1) people i.e., now we remove the last person. First case is: if kj = (j - 1), that means that the last (i-th) gondola contained one person but now since the last person has been removed some other person must take his place for the last gondola since no gondola can be empty. So, in this case kj - 1 < kj.
Now, to the more general case where we have kj < (j - 1) i.e., the last gondola contained more than one person. When we remove the last person, the unfamiliarity value of the last gondola decreases. Now suppose that shifting some person from the last gondola to the one before it reduces the unfamiliarity value. If it were the case, the same change could have been affected when we had j people with i gondolas and then for that case the optimal point would have been something > kj, which is a contradiction to our assumption that kj is the optimal point for j people. This means that no person can be moved from the last gondola to the one before it in the case of (j - 1) people.
But there is no denying the fact that people may move from the second last gondola to the last gondola since it may be the case that suppose the j-th person had a large unfamiliarity with the person who was put at the last of (i - 1)st gondola but now since the j-th person has been removed, the person in the last of (i - 1)st gondola may be moved here, which may reduce the overall unfamiliarity, which shows that kj - 1 may be lesser than kj.
The above statments show that kj - 1 ≤ kj which is indeed the monotonicity property that we had to prove.
Code available Setter's for DIV1 A — Ceil and Robot here: https://github.com/cgy4ever/cf190/blob/master/D1A.cpp
Can someone explain the solution to Div2 D(Div 1 B) using min cost maxflow in more detail. I understood the meaning of the costs and capacities assigned to the edges. But how does the implementation guarantee that the dummy node with outgoing capacity 100 will only be taken if all the nodes on Jiro's side are taken. I have been using min cost flow templates as a black box till now. Is it advised to know the implementation in depth so as we can modify it in the problems ??
http://codeforces.com/contest/321/submission/15137073
http://codeforces.com/contest/321/submission/31059563
Have a look at these two codes, they are almost same(except for some minor implementation differences). Why is the latter one far slower?
In DIV2D : can someone please explain me what this line means "There always exist an optimal solution that: If Ciel's two card X's strength > Y's strength, and X, Y attacks on A and B with the same position, then A's strength > B's strength. We already use this observation in above solution."?
A different and intesesting solution for Div 1 E. Using lambda optimization technique, one can get an O(N^2 * log(X)) solution when X is the sum of the matrix entries. However, this is still (slightly) too much time and I've got TLE in test 44 54320091.
With some cheating and luck I've optimized my solution and got AC with running time O(N * logX * 500) 54320008
I wonder if there's a working solution in O(N * logX * logN) exploiting the monotonous property of the DP in the function findOpt, let me know if you have one!
can you please tell me what is lambda optimization technique
In Div1B DP solution, what is the need of the fourth state: killall. If we just take first 3 states, will it not take into consideration the case where all the cards are attacked? I wrote a solution based on the first 3 states but it is giving WA on test case 34. Please help.
In div 1 E, Author wrote: Let opt[i][j] = the smallest k such that dp[i][j] = dp[i][k] + cost(k+1...j) Then intuitively we have opt[i][1] <= opt[i][2] <= ... <= opt[i][n].
Can anyone explain how is that intuitively correct!!?
Can't ceil the commander be solved by appointing commander in accordance with level of nodes?
No IMO that might not work in few cases like height exceeds 26. I dont know whether to use center or centroid or anything. This problem just made me confuse even more. I am damn sure that I will confuse again.
Problem C is excellent since I dont get the solution nor code.How much you irritate me,I will ensure that I play according to my rules
kudos to probelem seeters and escpeciaally the broken link to code was amazing surprise. But Destroying a powerful scene is more satisfying than this but will it work again ? That remains to be question for another What If
Can someone please explain the solution to Div2 D(Div 1 B) using min cost max flow?