Test Round and its analysis were prepared by snarknews and Gassa. Problems of the Test Round have already been used before in different competitions. The following rounds will consist of new original problems, and you can still register and compete in the Qualification Round.
During the round a lot of participants tried to make "blind" submits, from time to time even going to the top places, but as the system tests showed with only one problem solved in fact.
By the end of the round tourist was at the first place with all problems but B submitted "blind". vepifanov was at the second place with A, C and D submitted "blind", but B and F — submitted "open" (both with a wrong attempt), Anton_Lunyov was at the third place with only C submitted "blind". All other participants had less than 5 problems solved. After the system tests it turned out that tourist had a wrong solution for A, and vepifanov had a wrong solution for D. So, the only participant who solved 5 problems was Anton_Lunyov. tourist got second place, vepifanov was third.
It is a bit strange that problems B and E, although their solutions don't require special knowledge, remained mostly "unclaimed": all participants who solved these problems were in the top-3 with tourist solving E, Anton_Lunyov and vepifanov solving B.
It also turned out that file input and output can be an obstacle for the participants: 90% of questions were concerned with this. So we decided not to use file input and output in the future rounds of Yandex.Algorithm.
Problem A (Circles)
This problem is an advanced variant of a problem that was used in the 0th (pilot) season of OpenCup which happened in May of 2004. It can also be considered an easier version of a problem used in the Moscow Grand Prix of OpenCup in 2005.
Using the formula for area of triangle S = abc / 4R, we obtain R = abc / 4S, where a, b and c are lengths of the triangle's sides. Taking into account that the vertices of triangle have integer coordinates, we conclude that squares of lengths of the sides and doubled triangle area are integers. So, R2 can be computed exactly as an integer fraction 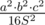 .
.
As the coordinates do not exceed 1400, numerator doesn't exceed 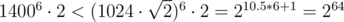 , so it fits into unsigned int64. To compare such fractions one has to either use long arithmetics or use modular arithmetics or compute GCD or store high-order number part separately...
, so it fits into unsigned int64. To compare such fractions one has to either use long arithmetics or use modular arithmetics or compute GCD or store high-order number part separately...
We point out that type double is insufficient even without considering the errors of computation: there exists an example of two triangles with circumscribed circle radiuses differing by less than 2 - 52. For example, triangles with vertices (0, 0), (1312, 164), (134, 1372) and (0, 0), (1351, 169), (106, 1317).
The example above was foundf using the following approach: fix one of the vertices at (0, 0) and the other two at (1400, 0) and (0, 1400). Bruteforce the coordinates of the last two points in some neighborhood, compute the circumference radiuses, sort them and find the minimal difference between two adjacent values.
As we expected, there were a lot of failed submissions for this problem which tried to solve problem using doubles and "search for espilon". Most participants who thought of exact solution right away didn't have problems with implementation.
Problem B (Three Fractions)
This problem was first used in the Moscow Grand Prix of OpenCup in 2005. That version was simpler: it didn't have multitest.
The easiest is to solve this problem using precalc.
Under the given restrictions on n and on the queries number it is reasonable to precalculate the full table of answers. If n is composite number and the problem is solved for all prime numbers less than n, then represent n as product n = a·p where p is prime. Then 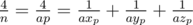 . So it is sufficient to precalculate answers for all prime n and for n = 4 and then compute the answers for composite n.
. So it is sufficient to precalculate answers for all prime n and for n = 4 and then compute the answers for composite n.
Let's make a very rough estimate on c and b. As 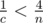 , then
, then 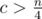 . As a > b > c, then
. As a > b > c, then 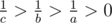 , so
, so 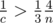 and
and 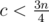 . Using the same logic
. Using the same logic 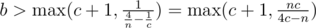 and
and 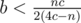 . So, let us bruteforce through all prime n, all b and c in the ranges we found above and check whether 4bc - nb - nc divides nbc. If it does, the answer can be found as
. So, let us bruteforce through all prime n, all b and c in the ranges we found above and check whether 4bc - nb - nc divides nbc. If it does, the answer can be found as 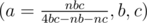 .
.
Such precalc takes less than a minute even using a very slow CoreDuo 1.6Ghz. One can just store b and c in the code. That was code size won't exceed 50k, which is less than source limit.
Another way is to bruteforce c and try to represent difference  as a sum of two "egyptian" fractions using Fibonacci's algorithm. This solution passes the Time Limit without precalc.
as a sum of two "egyptian" fractions using Fibonacci's algorithm. This solution passes the Time Limit without precalc.
This problem is a particular case of famous mathematical problem — Erdos-Straus conjecture. It is not solved in the general case, but there are solutions for all n ≤ 1014.
For those who appreciate constructive solutions — some formulas.
- If n = 3k + 2, we get
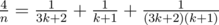 ,
, - If n = 4k, we get
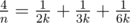 ,
, - If n = 4k + 2 and k > 1, then
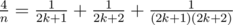 ,
, - If n = 4k + 3, we get
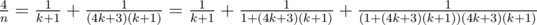 ,
, - If n = 8k + 5, we get
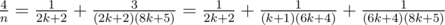 .
.
So, there is no explicit formula only for n = 24k + 1.
Problem C (Select The Digits)
This problem was first used at a school informatics circle in Saint-Petersburg Anichkov Palace in 2006.
This problem is rather simple and allows for many different ways of solving. Let us name a few. Below, we assume that s is the given string and res is the result we seek.
Solution 1
We can simply look over all quadruples of positions we select. Here is a sample of code in Pascal:
res := 9999;
for i := 1 to 5 do
for j := i + 1 to 6 do
for k := j + 1 to 7 do
for l := k + 1 to 8 do
res := Min (res, StrToInt (s[i] + s[j] + s[k] + s[l]));
Solution 2
In a high-level programming language, there could be tools which do all the dirty job related to searching by themselves. Here is a solution in Python looking over all combinations of four elements:
res = "".join (min (itertools.combinations (s, 4)))
Solution 3
The search could be organized recursively. Here is a function in Java taking two parameters: position p in the string s and number of positions q we have yet to take. The function is called from the main program like recur (8 - 1, 4) and looks over the positions from back to front.
int recur (int p, int q) {
if (q < 0 || p + 1 < q) return 9999;
if (p < 0) return 0;
return Math.min (recur (p - 1, q),
recur (p - 1, q - 1) * 10 + s.charAt (p) - '0');
}
Solution 4
The problem can be solved by dynamic programming. The two parameters are number of visited positions i and number of selected positions j. The value of target function f(i, j) is the minimal number which can be obtained. There are two transitions from each state: first, we either select or drop the current position, and then we move to the next position in string s. Below is a program in C/C++ demonstrating the approach. The answer is contained in cell f[8][4].
memset (f, 0x3F, sizeof (f));
f[0][0] = 0;
for (i = 0; i < 8; i++) {
for (j = 0; j <= 4; j++) {
f[i + 1][j] = min (f[i + 1][j], f[i][j]);
f[i + 1][j + 1] = min (f[i + 1][j + 1],
f[i][j] * 10 + (s[i] - '0'));
}
}
Problem D (Product of Different)
This problem was first used at a school informatics circle in Saint-Petersburg Anichkov Palace in 2009.
Let us start by presenting a test which had the number 15: n = 112 500 = 22·32·55. Its complexity lies in the fact that we can not choose divisor 2·3 = 6: in that case, the total number of divisors will be no more than six. Instead, we should choose the following factorization into seven factors: 112 500 = 1·2·3·5·10·15·25.
This is the minimal test which breaks some simple yet wrong solutions. One of them is to greedily choose the divisors, starting with the smallest possible, as long as after we add the next divisor d, the remaining number is strictly greater than d. On this test, it finds divisors 1·2·3·5·6, and then tries to factor 625 = 54, but neither 5 nor 25 = 52 could be taken.
The author's solution is an exhaustive search. A trivial recursive brute-force search which considers divisors up to  in increasing order manages to pass in under a second. The following function in C/C++ must be run as
in increasing order manages to pass in under a second. The following function in C/C++ must be run as recur (n, 1, 0). It writes the number of different divisors into res and the divisors themselves into the array best. The parameters have the following meaning: n is the number remaining to be factorized, k is the lowest possible value of the next divisor, and cur is the number of divisors already selected.
void recur (int n, int k, int cur) {
if (res < cur + 1) {
res = cur + 1;
now[cur] = n;
memmove (best, now, sizeof (best));
}
for (int d = k; d * (d + 1) <= n; d++)
if (n % d == 0) {
now[cur] = d;
recur (n / d, d + 1, cur + 1);
}
}
How does one estimate how fast is such a program? We can note that the answer is rather small: as the product of the first 13 positive integers is greater than 109, the answer is not greater than 12. This means that the first if will be triggered no more than 12 times. Another useful fact is that the numbers up to 109 have no more than 1344 different divisors each (http://oeis.org/A066150).
The easiest way is to write a program to give a crude upper bound on the number of divisions and or remainder calculations (example in C/C++). Here, n is the number remaining to be factorized, and k is the lowest possible value of the next divisor.
int count (int n, int k) {
int res = 0;
for (int d = k; d * (d + 1) <= n; d++)
res += 1 + count (n / d, d + 1);
return res;
}
This program differs from the actual solution: here, we step into recursion on every iteration of the cycle by d, and in the actual solution, we call recur only when n is evenly divisible by d. On the other hand, it allows us to use the maximal possible value of n to get an estimate (albeit crude) of the worst case, instead of searching for some large number with many divisors which make the real program run as slow as possible.
If we call count (1000000000, 1) the result will be 151 631 365. If we account for the fact that division by unity can be treated separately and start our search from divisor 2, the upper bound will be the result of calling count (1000000000, 2), it is 75 815 682 (half of the above). In fact, we know that the square root of about 109 is about 30 000, and the number of divisors less than the square root is no more than 1344 / 2 = 672, it is obvious that the actual number of divisions will be a few times less. The maximal number of divisions and/or remainder calculations in all jury tests turned out to be 15 395 811.
There are faster ways to do an exhaustive search as well. For example, instead of looking over all numbers up to the square root of n, we can just look over all divisors of n which can be found in advance in 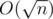 time. Also we can first decompose n into prime factors and then search for divisors as tuples of powers for each of these prime factors.
time. Also we can first decompose n into prime factors and then search for divisors as tuples of powers for each of these prime factors.
Problem E (Table of Championship)
This problem is an version of problem from the Moscow Grand Prix of OpenCup 2005 adapted for memory limit=64 MiB. In the initial version memory limit was 3Mb and lengths of team names didn't exceed 15 symbols.
There are two cases: when all three lost numbers are in the same line and when at least one of them concerns a different team (or less than 3 numbers were lost).
Let's denote the number of matches played by i-th team by Pi, number of wins by Wi, number of draws by Di, number of losses by Li and number of points by Si.
Then the following equations hold: Wi + Di + Li = Pi and 3Wi + Di = Si. If not all 3 numbers lost concern the same team, we have to solve several systems of linear equations with not more than 2 variables.
In the case when all 3 lost numbers concern the same team, we get one more equation from the fact that the total number of wins of all teams equals the total number of losses of all teams. Wi + W - i = Li + L - i where W - i is the total number of wins of all teams but i-th and L - i is the total number of losses of all teams but i-th.
So the unique restoration of numbers is always possible.
The main difficulty in this problem is that the whole table doesn't fit into memory.
So one has to read input file twice: first to build the system of equations (while reading, we sum Wi and Li to build the system of equations in the second case), second to find the line which holds the answer.
Problem F (Taxis)
This problem was first set by polish authors and was first used at the first stage of All-Poland school olympiad 2012-2013.
Obviously, either one can go the path from the taxi base to the destination without switching taxis or it is impossible to get to the destination (as the taxi that will arrive at destination has to go through the whole segment from the taxi base to the destination). So let's "reserve" a taxi with the minimum fuel sufficient to go from the taxi base to the destination. Also let's construct the farthest point from the destination from which this car can get a passenger and drive him to the destination. If the taxi base is at the destination, no "reservation" is made.
Then let's sort cars which are not "reserved" by descending amount of fuel and each time choose the car with the maximum fuel. We will now prove that this algorithm gives a solution which is not worse than any other possible solution. Suppose we first use a taxi with fuel X1 and then a taxi with fuel X2, and the passenger starts at distance a before the taxi base. Then the passenger will go (X1 - a) + (X2 - (2a - X1)) = 2X1 + X2 - 3a kilometers. If X2 > X1, then if we change X2 and X1 we'll see that the distance travelled increased. If the car with the largest fuel left can't go already (or there are no cars left that are not "reserved" before the passenger gets past Z), then it is impossible to get to the destination.
If passenger is at point Z or closer to the destination at some point, he can already arrive at the destination using the "reserved" car. We also have to check if passenger can get to the destination right away, without using the "reserved" car.












