General comments
Broadly speaking, problems A-B-C-D were "div2 problems", while F-G-H were "strong grandmaster problems" (with E staying in the middle). I did not expect anyone to solve all the problems and thus I decided to give the scoring F+G=H (so that maybe someone would have solved H).
Many of the problems (A, C, D, E, G) admit multiple solutions. Sometimes the core of the solution is the same (C, D) and sometimes the solutions are truly different (A, E, G).
If you are an experienced participant, I would like to hear your opinion on the problems. Feel free to comment on this post or send me a private message.
Overview of the problemset
The easiest problem of the contest, A-Avoiding Zero, is about rearranging an array of numbers. It is intended as a very easy problem that still requires to think. Then, in B-Chess Cheater an intuitive (but nontrivial to prove) greedy approach is the way to go. C-The Hard Work of Paparazzi is a classical dynamic-programming problem with a twist. D-Unshuffling a deck is a constructive problem with a multitude of possible solutions (all somewhat similar). The difficulty difference between D and E-Xum is pretty large. Problem E asks to produce the number $$$1$$$ (starting from a given number) using only the addition and the xor. A super-clean mathy approach is possible, but also a huge amount of (vastly different) randomized approaches (clean and not so clean) can lead to the solution.
Problems F, G have a similar difficulty. They are very different, so participants could choose which one to attack depending on their taste. Problem F-Boring Card Game asks to reconstruct the moves of a game given the final situation. Even if it looks as one more constructive problem, it is not. The crux of the problem is finding a criterion for the admissibility of a final situation and then noticing that a naive greedy algorithm produces a sequence of moves generating such final situation. It requires quite a bit of thinking, but then the implementation is trivial. Problem G-One Billion Shades of Grey has the clear smell of a flow, and indeed it is a flow problem! There are two possible approaches: either you have a clever idea, or you apply some advanced classical theory followed by a certain amount of optimizations. Compared to problem F, in G the ideas are more standard but the implementation is not immediate. Since the statement is extremely simple, it is possible that some versions of this problem are known (and I actually found at least one research paper considering something similar). I decided that the problem is beautiful enough to take the risk.
Finally we have H-Prison Break which is much harder than all other problems. Even if it is a variation over the well known Cat and Mouse problem, knowing the solution to the latter is not very helpful. It is a very nonstandard problem and a mix of mathematical insight and ability to handle an involved implementation is necessary to get accepted.
Problems F, G have a similar difficulty. They are very different, so participants could choose which one to attack depending on their taste. Problem F-Boring Card Game asks to reconstruct the moves of a game given the final situation. Even if it looks as one more constructive problem, it is not. The crux of the problem is finding a criterion for the admissibility of a final situation and then noticing that a naive greedy algorithm produces a sequence of moves generating such final situation. It requires quite a bit of thinking, but then the implementation is trivial. Problem G-One Billion Shades of Grey has the clear smell of a flow, and indeed it is a flow problem! There are two possible approaches: either you have a clever idea, or you apply some advanced classical theory followed by a certain amount of optimizations. Compared to problem F, in G the ideas are more standard but the implementation is not immediate. Since the statement is extremely simple, it is possible that some versions of this problem are known (and I actually found at least one research paper considering something similar). I decided that the problem is beautiful enough to take the risk.
Finally we have H-Prison Break which is much harder than all other problems. Even if it is a variation over the well known Cat and Mouse problem, knowing the solution to the latter is not very helpful. It is a very nonstandard problem and a mix of mathematical insight and ability to handle an involved implementation is necessary to get accepted.
Hints
A
Hint 1
If $$$a_1 + \cdots + a_n = 0$$$, then the answer is NO.
Hint 2
If $$$a_1 + \cdots + a_n \not=0$$$, then the answer is YES.
Hint 3
If $$$a_1 + \cdots + a_n > 0$$$, then there is a rearrangement such that all prefix sums are strictly positive.
B
Hint 1
The score is $$$2\cdot\texttt{#{wins}} - \texttt{#{winning_streaks}}$$$.
Hint 2
You shall minimize the number of disjoint winning streaks.
Hint 3
Fill the holes between winning streaks.
C
Hint 1
Find an $$$O(n^2)$$$ dynamic-programming solution.
Hint 2
The city is relatively small (i.e., $$$r\le 500$$$).
Hint 3
If $$$j>i + 2r$$$ then it is possible to go from the $$$i$$$-th appearance to the $$$j$$$-th appearance. Use this observation to optimize the $$$O(n^2)$$$ solution to $$$O(nr)$$$.
D
Hint 1
If two consecutive cards have consecutive numbers (in the right order) then you can "merge them".
Hint 2
Consider only moves with small $$$k$$$.
Hint 3
Find one move that increases by at least $$$1$$$ the number of adjacent cards with consecutive numbers.
E
There are two different solutions.
Solution 1:
Solution 2:
Solution 1:
Hint 1
Write a number $$$y$$$ coprime with $$$x$$$.
Hint 2
Write the gcd between $$$x$$$ and $$$y$$$ (that is $$$1$$$).
Hint 3
Bezout's Theorem.
Hint 4
If $$$a = b+1$$$ and $$$b$$$ is even, then $$$a\wedge b=1$$$.
Solution 2:
Hint 1
Keep a basis of the numbers that are the xor of a subset of the numbers on the blackboard (i.e., the xor-subspace generated by numbers on the blackboard).
Hint 2
Make some random choices.
Hint 3
If $$$x=2^{19} + 1$$$, then it is necessary to write a number $$$>10^{11}$$$ on the blackboard.
Hint 4
Choose randomly two numbers from the xor-subspace and write their sum on the blackboard.
F
Hint 1
Solve the problem without the constraint of alternating turns.
Hint 2
The final situation is achievable if and only if it is achievable without alternating turns but with Giada taking the last turn.
Hint 3
Use a greedy approach to take care of the alternating turns.
G
There are two different solutions.
Solution 1:
Solution2:
Solution 1:
Hint 1
Solve the problem when the already painted tiles have only two shades.
Hint 2
Formulate the problem as many min-cuts problems.
Hint 3
Update the max-flow repeatedly to compute quickly enough the many min-cuts.
Solution2:
Hint 1
Formulate the problem as a linear-programming problem.
Hint 2
Compute the dual of the problem.
Hint 3
Use the shortest-augmenting-path algorithm to compute the min-cost maxflow and optimize Dijkstra as much as possible (and simplify the graph as much as possible).
H
Hint 1
Solve the problem with one guard instead of two.
Hint 2
If the prisoner can escape, his strategy is easy.
Hint 3
If the prisoner can escape, then he should go to a point on the climbable walls and either escape immediately or go toward one of two different points on the climbable walls and escape there.
Hint 4
The prisoner can escape if and only if there are three points A < B < C on the climbable walls such that a guard cannot go from B to A as fast as the prisoner and a guard cannot go from B to C as fast as the prisoner.
Hint 5
Binary search on the answer.
Hint 6
Fix the sides where A and B are. The points B such that there is a good point A form an interval, determine the interval.
Hint 7
Be optimistic and use ternary-search (or be less optimistic and solve a bunch of quadratic equations).
Solutions
A
Tutorial is loading...
Solution code B
Tutorial is loading...
Solution code C
Tutorial is loading...
Solution code D
Tutorial is loading...
Solution code E
Tutorial is loading...
Solution code F
Tutorial is loading...
Solution code G
Tutorial is loading...
Solution code H
Tutorial is loading...
Solution code 









Awesome editorial and even awesome questions. After this round, I feel like practicing more now.
I really liked this contest. All problems between A and E are well-balanced. They are not almost ad-hoc, and they are not stupid realization. Ideal balance! Thanks for this round!
But i must to say, that in my opinion it is makes no sense to do score distribution like 500-750-1000-1000-1500
thanks for blazing fast editorial. Loved the problems <3
How did you love the problems while you haven't even submitted any?
lol get downvoted xD.
For problem C
This is a classical dynamic-programming task with a twist.Which task does this refer to?It's quite similar to the longest increasing subsequence, but the condition to pick the previous element is $$$dist(i, j) \leq t_j - t_i$$$ instead of $$$a_j > a_i$$$.
There is the use of upper_bound in the regular longest increasing subsequence problem of O(nlog(n)). But in this problem how I make a binary search. (dist(i,j)≤tj−ti) can give only true or false, not greater than or less than. Actually, I can't be sure my temp array will be sorted.
The "twist" is not binary search: it's that $$$t_j - t_i \geq j - i$$$ and $$$dist(i, j) \leq 2r$$$, hence the condition is true for each $$$i, j$$$ such that $$$j - i \geq 2r$$$.
Oh, thanks. Got it :)
TheScrasse PrantaSaha Can someone please explain what 2*r means?
The idea is that if |k−i| is big, then i and k are always compatible. More precisely, if k−i ≥ 2r then tk−ti ≥ 2rHow can we be so sure about this?Since the side of the grid is $$$r$$$, the distance of the farthest vertices (two opposite corners) is $$$2r - 2$$$.
After reading your comment a was able to understand editorial Thanks
I think the task is Longest increasing subsequence:- https://www.geeksforgeeks.org/longest-increasing-subsequence-dp-3/
it fits easily in the time-limit.it doesn't...I have quickly checked your last submission during the contest, it seems to me that it is $$$O(n^4)$$$ (you are calling janusz.dinic() $$$O(n)$$$ times). If I am wrong (which is very likely), sorry.
If you implemented the first solution in the editorial in $$$O(n^3)$$$ and you got time-limit-exceeded, I am sorry, that was of course not intended.
Since I am here, let me comment a bit more on the time-limit of problem G. I have the feeling that in many flow problems, the general mentality is "let's ignore complexity because any flow implementation will work". In this problem this was not true. A nontrivial amount of contestants got TLE because of this. Before the contest I thought a lot about this time-limit, because I knew it would have generated quite a bit of struggling. The fundamental reason why I decided to keep it as it is, was to avoid $$$O(n^4)$$$ solutions passing and to award contestants that instead of using fancy (but with bad complexity/terrible constants) implementations of the flow algorithm were implementing the good old Ford-Fulkerson (proving its complexity!). It might be that this choice generated more suffering than joy... but as always it is much easier to judge a posteriori.
I run dinic() $$$n$$$ times, but in total, I'll push only $$$O(n)$$$ units of flow (I'm using the network from the previous iteration).
After the contest, I've changed Dinic to work like Ford-Fulkerson, so it doesn't run bfs. It was a bit faster, which was enough.
That is unfortunate and it is my fault. Hopefully next time I will not make the same mistake.
Anyone wasted an hour in B?
I was stuck on B for the entire contest after solving A in 00:04 :'(
I solved A in 00:14 and B in 02:10. That was a hard time.
I solved B at 2:59 .
I couldn't solve B. I got the idea right but I couldn't prove it. Feeling lame especially when you are(were) an expert.
In parallel universe.
If $$$a=b+1$$$ and $$$b$$$ is even, then $$$a^b=1$$$.
In Hint $$$4$$$ of the first solution of problem $$$E$$$, maybe it should be $$$a\oplus b=1$$$($$$\oplus$$$ denotes xor)...
Also in Hint $$$3$$$ of the second solution, it should be $$$2^{19}$$$ but not $$$2^19$$$.
Thank you, fixed.
Many of them could have got ac on D if it were 2*n steps,lol. By the way,thanks for a great contest.Liked it. Thanks for strong pretests
Me :Could only solve one, feeling low...
Also Me : After reading the overview of problemset...I am glad I solved A.
This is peak editorial writing. From giving some extra time to the ones who were really close to getting AC on H to writing multiple hints for us to be able to figure out the rest of the solution by ourselves. Great work dude!
I love that, I was close to getting C and only read the hints and was able to solve it. A good way to learn is by using hints instead of revealing the whole solution.
Thanks for the awesome Tutorial keep it with hints its such a good way of learning and explanation :D !
The way of presentation of the Editorial is very Nice. Going through the Hints before The Actual Solution really helps in learning. I request all editorial should be posted like this (Hints and Then solution).
I have lost more than 200 rating points in the last 3 contests, Don't really know what's happening :/
You just reached where you actually belonged :P
hahaha, Not sure about you. But I don't belong here. Its time to increase my rating now I think
how it is going?
Great format for the editorial! Loved the bunch of hints before the elaborated solution. Thank you!
it would have been better , if the editorials were given with the problems in the contest.
Here are video solutions for A-E, as well as complaining about gaining rating (apparently)
sorry for such a silly question but why am i getting TLE here? 95114705 I tried to form all possible permutations coz the constraints were very small. But still i got TLE. If anyone got time a slight help would be great. Thank you. Have a good day
what is the value of 50! ?(50 factorial).
Can anyone tell why my solution is incorrect for Problem — B ( Chess Cheater )? My approach :
Link to submission : Can anyone point out the mistake kindly? Thanks in advance :)
I had the same solution in contest. Consider the case
2 0
WW
However, this isn't what happens in the code — you sort by length first, then consider the type.
Yeah, I just figured it out after posting the comment :'3 Thanks for the prompt reply anyway. I guess sometimes we rookies just lost, tearing out hair over trivial mistakes which then builds frustration and tosses the self confidence into a black hole temporarily!
Or just have poor debugging skills...
C was much harder than D for me.
Depends. If someone has good DP knowledge, C was way more easier than D and less time consuming. I took like one hour and half in D which I was too late to solve in contest so I solved it and AC after contest.
Nice editorial! It would be great if we can have hint on all the future editorials! (but that would be time consuming for the writer)
I am glad that the hints were so appreciated. I have just followed a suggestion by Errichto.
In any case, writing hints requires way less effort and time than writing the editorial. So, I would advise any problemsetter who has some spare time before the contest (or also during the contest!) to write hints.
Great Set of questions. Even the editorial in this format is very informative and help in logic building.
This is the toughest round for me so far.
Same, couldn't solve C or D ..
Found solutions to D and E but couldn't code it, and failed B due to a very stupid bug.
Solved C at Last moment just one step missed. Chain will continue.
I am learning and then forgetting what I learnt !! and sometimes I think I do not learn anything from problem.sometimes I even feel there is no such thing as learning in CP bcoz every time a new problem will come up.I dont know when I will see the twists of problem. I am not sure whats the point of even solving problems bcoz those problems wont repeat themselves and you can't apply it to other problems. For Instance Take Problem C.It is already closer to standard problem or problem which I solved but could'nt move an inch towards solution
There is an elementary solution to E which does not use Bezout's Theorem.
Let ^ denote the XOR operation.
We can assume that the bit that is worth $$$2$$$ is off in $$$x$$$, because if we get an $$$x$$$ such that the bit that is worth $$$2$$$ is on, we can take $$$x' = (x$$$ ^ $$$2x)$$$ (this will be crucial later).
The claim is that we can find a multiple of $$$x$$$, such that its last $$$\lceil\log_2(x)\rceil$$$ digits are zero, except for the last one, which is a $$$1$$$.
We do this by saving all $$$x\cdot 2^k$$$ for $$$1 \leq k \leq \lceil\log_2(x)\rceil$$$ which we can do in $$$\lceil\log_2(x)\rceil$$$ steps, then constructing a number $$$q$$$ by first taking $$$x$$$, then going from $$$i = 1$$$ to $$$\lceil\log_2(x)\rceil$$$, and if $$$q$$$ has the bit that is worth $$$2^i$$$, then we xor $$$p$$$ with $$$x\cdot 2^i$$$, which has that bit as one, and all smaller bits as zero.
Now $$$p$$$ is some prefix, then $$$\lceil\log_2(x)\rceil$$$ zeroes, then a $$$1$$$ in binary.
The next claim is that $$$(p + x)$$$ ^ $$$(p $$$ ^ $$$ x) = 2$$$.
This is true, because the first bits are the same it both numbers, so we need to only care about the last $$$\lceil\log_2(x)\rceil$$$ bits.
For $$$p $$$ ^ $$$x$$$ this is $$$x - 1$$$, for $$$p + x$$$ this is $$$x + 1$$$, and because the bit that is worth $$$2$$$ is off in $$$x$$$, the XOR of these two numbers is $$$2$$$.
Now, having $$$2$$$, we construct $$$2^i$$$ for $$$i = 1$$$ to $$$\lceil\log_2(x)\rceil$$$, and then we can just turn the bits that are not worth 1 in $$$x$$$ off by XORing with the suitable power of 2.
For B, I used the idea of finding the contiguous substring with maximum consecutive Ws by performing at most k flips(where a flip is from W to L, L to W). Then I would calculate the winning score. I am getting the wrong answer on pretest2. Can somebody help me find out what's wrong with my solution?
Here is my code — void solve() { cin >> n >> k;
string s; cin >> s; vi A(n); fo(i,n){ if(s[i]=='W') A[i] = 1; else if(s[i]=='L') A[i] = 0; } // Now I find the contiguous substring with maximum consecutive 1s by doing at most k flips. int l=0, r=0, maxLen=INT_MIN, maxL, maxR, c=k; for(r=0,l=0; r<n; r++){ if(c<0){ while(l<=r){ if(c>=0) break; if(A[l]==0) c++; l++; } } else{ if(A[r]==0){ c--; if(c<0){ r--; continue; } } if((r-l+1)>maxLen){ maxLen=r-l+1; maxL=l; maxR=r; } } } int ans = 0, j = maxL; if(maxLen!=INT_MIN){ while(j<=maxR){ A[j] = 1; j++; } fo(i,n){ if(i==0){ if(A[i]==1) ans++; } else if(i>0 && A[i]==1){ if(A[i-1]==1) ans+=2; else ans++; } } } cout << ans << endl;}
Note that the solution might not be to create a single substring: consider the input
https://codeforces.com/contest/1427/submission/95152627
It turns out my problem was that I was simply losing too much precision when considering escaping through a very close point :(
Knowing that my answer is actually bigger than the correct one was enough to find the issue immediately.
Thanks for the contest!
Congratulations!
By the way, I had exactly the same bug when preparing the problem. I lost a full day on that!
Can you very briefly describe the solution? I'm dying to know how far away I was.
I assumed that it's enough to consider the prisoner to start from some point on the boundary and guards can then choose where they start. Iterate over segment of prisoner, ternary search his exact position there, one guard must stand at same position, iterate over segment of the other guard, ternary search his exact position, then check with Apollonius circles who wins (well, actually find the ratio for tie).
I have posted the editorial.
It's very similar to the editorial, but in a few words:
indeed, let's assume that the prisoner starts at the boundary. Then one of the guards must be in the same point or they'll escape immediately, so the other guard can guard only one of two segments that this point splits the boundary into. So if we compute the speed needed to catch the prisoner that runs to some point at the bottom part (via iterating over the segment we run to and using ternary search), the speed needed to catch the prisoner that runs to some point at the top part, and take the minimum of those two values, it will be a lower bound on the answer. Now we treat it as a blackbox function f(x) and try to find its maximum (I'm not sure ternary search within each segment is enough, so I had something slightly more general). I don't have a proof that the maximum of those lower bounds is the answer, I guess the editorial does :)
In the question C... I tried a code with dp approach but with some restriction (difference of index). It passed all the test cases.
But for this test case my code outputs 0 but the answer should be 1.
500 2
100 50 60
2100 500 500
Are the test cases of C weak or Am I wrong somewhere?
Submission link:- https://codeforces.com/contest/1427/submission/95152766
In problem C, I thought that R in the input is useless then tried solving the inequality tj — ti >= |xj — xi| + |yj — yi|, (tj > ti) to solve the problem in n*log(n) time but didn't come up with the solution, is there any such faster solution possible?
My solution for problem G seems to be a weird modification of the standard solution.
I do binary search on the candidate values, run min-cut, then divide the vertices into two halves. Thus there will be $$$O(\log n)$$$ layers, each consisting a total of $$$O(n^2)$$$ vertices and edges. The complexity will be $$$O(n^3\log n)$$$. (Since Dinic's algorithm works in $$$O(E\min\{E^{1/2},V^{2/3}\})$$$ on networks with unit capacities)
Difficulty of 'B' should not be less than 1500
Another deterministic solution of E:
Step 1: Let $$$p \in N$$$ be the unique number such that $$$2^{p-1} < x < 2^{p}$$$. Write $$$2^p x$$$ and $$$(2^p - 1) x$$$ on board with $$$O(p)$$$ operations.
Step 2: Write $$$(2^p x) \oplus ((2^p - 1) x) = 2^{p+1} - x$$$ on the board. Then, write $$$x+ (2^{p+1} - x) = 2^{p+1}$$$ on the board.
Step 3: We can write $$$2^i$$$ for all $$$i \ge p+1$$$ on the board. Write $$$2^p$$$ by using xor operations for all the bits of $$$2^p x$$$ except $$$2^p$$$.
Step 4: Write $$$(2^{p+1} - x) \oplus (2^p) = (2^p - x)$$$ and repeat the steps with new $$$x = (2^p - x)$$$ while $$$x \ge 1$$$. New $$$p$$$ of new $$$x$$$ is strictly smaller than current $$$p$$$, so it repeats at most 20 times.
Can dynamic programming in Problem C be done with recursion and memoization? If yes, how? Please help.
Yes, taking help from the "alternative optimization" in the editorial, you can solve it using recursive DP, just make sure you don't consider more than $$$4*r$$$ of the next celebrities.
That being said, the iterative approach is cleaner and easier, so try to practice that instead.
Alright! I'll try both. Thank you! :)
My O(n * r) iterative Java solution is getting a TLE (I haven't used the alternate optimization, but that's shouldn't be necessary right?)
https://codeforces.com/contest/1427/submission/95385701
I saw solutions in C++ do the exact same thing and get an AC :-(
Problem D is actually very easy if you realize the operation is same as reversing each deck individually and reversing the entire array. Since you can fix the reversing of the entire array with one operation, the problem is reduced to "sort an array with at most N subarray reverses", which is easy
Good one!
I would be thankful if you can give a quick example.
Let's say array is $$$[1, 3, 4, 2]$$$ and you choose decks $$$D_1 = [1, 3]$$$ and $$$D_2 = [4, 2]$$$. Then, after the operation it becomes $$$[4, 2, 1, 3]$$$. This is the same as these two operations applied, one after another:
Ignoring the second operation, according to the link I posted to the solution of the reduced problem, you would choose decks with sizes:
Now, to consider the second operation, you just need to keep a flag if the array is reversed or not. If it is, you reverse the decks you print. If by the end this flag is true, you print one last time: $$$[1, 1, 1, 1]$$$ (this will only reverse the array).
Hope it is clear now!
In the editorial for problem A, it's conjectured that a random shuffle works with probability at least $$$\tfrac1n$$$ (assuming the sum of all the numbers is nonzero). This is true, and here is a proof. The key claim is that, given any shuffle, some cyclic permutation of it works. This easily implies the desired result.
Suppose that the claim is false for some shuffle $$$a_1,\ \dots,\ a_n$$$ (so $$$a_1 + \dots + a_n \ne 0$$$). Interpret all indices modulo $$$n$$$. Since no cyclic permutation of this is valid, for any $$$k$$$, there exists some $$$f(k)$$$ such that $$$a_k + a_{k+1} + \dots + a_{f(k)-1} = 0$$$.
Thus, we have a function $$$f$$$ on the integers modulo $$$n$$$. (Formally, we have $$$f\colon \mathbb Z/n\mathbb Z \to \mathbb Z/n\mathbb Z$$$.) Thus, this function has a cycle, say $$$t_1 \to t_2 \to \dots \to t_k \to t_1$$$.
This gives us the $$$k$$$ relations $$$a_{t_1} + \dots + a_{t_2-1} = 0$$$, $$$a_{t_2} + \dots + a_{t_3-1} = 0$$$, $$$\dots$$$, $$$a_{t_k} + \dots + a_{t_1-1} = 0$$$. Summing these all up, we get $$$c(a_1 + \dots + a_n) = 0$$$, where $$$c$$$ is the number of "revolutions." Thus $$$a_1 + \dots + a_n = 0$$$, as wanted.
Very cool! If you don't mind, I will add a link to your comment in the editorial.
UPD: Added.
That’s okay with me. Thanks for the great contest!
I didn't get this. Will you please elaborate on it?
Recall that for each $$$k$$$, we have an $$$f(k)$$$ for which $$$a_k + a_{k+1} + \dots + a_{f(k)-1} = 0$$$.
Now draw an arrow from $$$a_k$$$ to $$$a_{f(k)}$$$ for each $$$k$$$. Since we have one arrow leading out of each term, there must exist a cycle of arrows. (To see this, imagine following the arrows: travel from $$$a_k$$$ to $$$a_{f(k)}$$$ to $$$a_{f(f(k))}$$$, etc. Then eventually we must revisit some term, which gives a cycle.)
Suppose the cycle takes $$$a_{t_1}$$$ to $$$a_{t_2}$$$ to $$$a_{t_3}$$$ to ... to $$$a_{t_k}$$$ to $$$a_{t_1}$$$. Now we can follow the last paragraph of the proof.
That's pretty good! I think the below also works as proof (correct me if I'm wrong).
In the case where n-1 numbers are 0 and one is non-zero, the only possible permutation that gives you an acceptable answer is when non-zero number comes first. Probability of that happening is 1/n. Probability will keep decreasing as you replace non-zero numbers with 0, so the lowest positive probability is 1/n.
I have a straight forward solution for E with no randomization or coprime numbers required.
Let k be the MSB of x. Notice that we can get 2^n * x for all n by adding x to itself and then repeating. Now, for any number on the board y, we can set all bits >= k equal to 1. We can do this by xor-ing 2^n*x to set each bit above k if it is not set for some appropriate n. So we just need to find two numbers for which, after setting all bits >= k to 1, all of the bits below k are the same, except the 1 bit. We can just check the first 3e6 multiples of x (no randomization required).
Submission: https://codeforces.com/contest/1427/submission/95156859
I solved problem C the way you suggested and thought that 2rn = 10^8 will not fit so I didn't implement it...
Did this happen to anyone else?
Sadly same thing happened with me, I was trying to think of applying segment tree on n but it got too messy. Hopefully I would have tried D first which was relative easier to me.
I implemented as said in the tutorial. Hope it helps :) Solution
Same. Was able to think O(nr) and was like 10^8? No that won't work.
95127605 I used random_shuffle for problem A because the constraints were small whereas everybody else used sorting. Is it my luck that my submission got accepted? Also, what are the chances that my solution won't work?
For E, I had similar solution to the gcd one, but the step of finding a co-prime pair is randomized. It randomly generates new numbers until it finds a co-prime pair. It too completes in $$$\le 100$$$ operations. 95149535
one of the best editorial. Loved it!!
if it is possible, try to keep hints option in every editorial .. it is so beneficially for a newbie like me :)
I like the solution to E with bezout theorem very much! Thanks for fast editorial.
Could you check pls what is wrong with my solution for C (WA15)
cin >> k >> n; vector<pair<ll,ll>> v(1e6+1, {-1,-1}); v[0] = {1,1}; for(ll i = 0; i < n; ++i) { cin >> t >> p >> q; v[t] = {p,q}; m = t; } vector<ll> dp(m+1, 0); sum = 0; for(ll i = 0; i < m+1; ++i) { if(v[i].first == -1) continue; if(i-k*2 > 0) { sum = max(sum,dp[i-k*2-1]); dp[i] = max(dp[i], sum+1); } for(ll j = i+1; j < min(i+k*2+1, m+1); ++j) { if(v[j].first == -1) continue; if(j-i >= abs(v[j].first-v[i].first)+abs(v[j].second-v[i].second)) { if(dp[i] || !i) dp[j] = max(dp[j], dp[i]+1); } } } mx = 0; for(ll i = 0; i < m+1; ++i) { mx = max(dp[i], mx); } cout << mx;Why is the approach at problem A correct???
I stupidly misread the constraints for D, and even more stupidly called my results vector in the solution "omgconstraints", as a way to punish myself for not reading constraints, by typing that name like 50 times. Given that my successful submission for D was 10 seconds before the contest ended, I cursed myself every time i typed "omgconstraints" rather than the usual "res" that I use. Had I known that these extra letters might have pushed cost me the problem, I would have definitely thought twice.
Hey, I have some problems with B.
Just Have a look at this test case and tell me how's the answer for this test case is 16.
1
12 2
WWLWLLWLWWWL
Ans:- 16 I think the answer should be 15
WWWWLLWWWWWL
Thank-you bro.
In problem C.Who can explain completely Hint 3 ?
I have already understood it!
Based on this contest, I believe that dario2994 is one of the best problemsetters on CF. Would love to see another contest from you!
Can someone explain step1 of the deterministic solution of Problem E . Particularly this line :- y=(2ex)^x=(2e+1)x−2e+1 and therefore gcd(x,y)=gcd(x,2e+1)=1
Who is an "experienced participant" in your view dario2994?
Anyone who participated in at least 10 contests and is able to enjoy a contest even if he gets a negative rating change.
.
Let me rewrite the statement.
Anyone who participated in at least 10 contests and is trying to improve even he doesn't improve
Hi, Can anyone help to understand why my solution of problem D works. Here is the link to solution : SOLUTION
Approach: I am counting the number of operations from 0.
When the parity of number of operation is even : In this case I select subarrays staring from first element till the elements are in decreasing order. When I find an element that is bigger than previous element, I stop and considers the chosen elements as a split. Now I start fresh from this element and repeat this process until I have some k splits. Now I perform the operation on them.
When the parity of operation is odd, I am doing the same process except I chose subarrays that are strictly increasing.
For example : Input:
5
4 2 1 5 3
Output:
2
3 3 1 1
4 1 2 1 1
Given 4 2 1 5 3:
Operation 0 : Parity = 0
We split as (4 2 1) (5 3)
New array : 5 3 4 2 1
Operation 1: Parity = 1
We split as (5) (3 4) (2) (1)
New array : 1 2 3 4 5
We get the sorted array.
I am not able to prove why this works. I saw this pattern during contest but forgot about the case that k should not be equal to 1. Is this same as the approach given in the editorial intuitively ?
This is what I did in problem D.
Idea: for 1<=i<n we get i and (i+1) adjacent keeping everything else(less than i) adjacent. (Similar to the editorials idea). Hence in at most n-1 moves we can get the array sorted and 1 extra move if the array turns out to be descending.
So let us say we have first i numbers sorted(descending or ascending). We have 4 possibilities.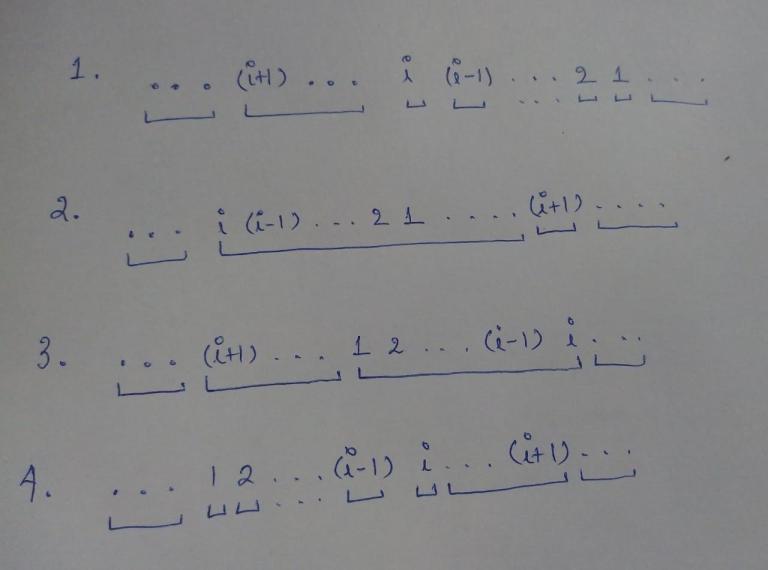
The indicated boxes are how we can achieve our idea.
After this the code is fairly simple.
As asked by the dario2994, I have some feedback to offer. Some of the below points are for the a part of community who miss no chance to rant the organisers. So here we go.(expecting a lot of hate from those who can't agree diverse thought process)
What I loved about the contest:
The contest in general was awesome. It was one those contests that kept me thinking about the problems for the entire time rather than reaching a point where one realises that later problems ain't their cup of tea. (Kudos for this because such contests are rare to find).
The contest had a vast range of problem. Many people are of the view that contest was filled with ad-hoc ones, but I beg to differ. I think we can call these problems as non-trivial/non-standard rather than ad-hoc. (I know lot of people would disagree to this)
The contest is an excellent example where the problem statement are not exactly short yet very interesting to read. I can't stress enough that length of problem statement doesn't matter as long as the description is to the point and doesn't make things messy to understand. As for me, I didn't loose interest in reading any statement and I read all of them (yes all until H) even though I knew I wouldn't be able to solve them realistically.(I expect most hate for favouring the length of problem statements).
The contest had excellent sample cases. I can bet that without such samples a lot people would have had series of WA on pretest for question B.
The contest had really high quality problem (even though I couldn't solve many problems doesn't take away the fact). I would genuinely like to appreciate the quality of the problems and beautiful ideas behind the solutions.
What I think could have made contest more interesting:
But overall, I'd place this contest in top 10-15 of all I have appeared in (appx 200 or more across various platforms). I'd sincerely appreciate the hard work of author and coordinators for making such a nice contest.
Thank you for the feedback (and don't worry about downvotes).
Regarding 4., I have to thank testers for this. Initially samples for B were much weaker and many testers complained.
So we are basically optimising $$$ O(n^2) $$$ dp solution for Problem C. My question is how do we optimize it if there is no $$$ \triangle{t} \ge 2\cdot{r} $$$. Won't it run on $$$ O(n^2) $$$ and give a TLE. Or am I missing something out? Thanks and Great Round.
Got it. $$$t(i)<t(i+1)$$$ that limits maximum iterations to $$$2r$$$ and complexity to $$$O(2nr)$$$.
I did come up with the $$$O(nr)$$$ solution for 1427C - The Hard Work of Paparazzi, but I thought it would not fit into the time limit :(
I use another optimization in problem C and also get accepted: 95139974 My brief idea is using
ans[i]to store the maximum photos can be taken when we already at i'th celebrity. We iterate from ans[n] to ans[1]. For each ans[i], instead of iterating all celebrities in [i+1, n], we use amapto record the ans[j] (j in [i+1, n]) in descending order, so we can just take the first celebrity that satisfies $$$|x_i-x_j| + |y_i-y_j| \le t_j-t_i$$$.For problem C, is it possible that two consecutive celebrities appear at the same intersection?
That has to be true for any test case where n > r * r according to the pigeon hole principle.
My solution for E:
I don't want randomised solutions because they carry a risk, but my thinking here is way more random. I have no idea why this works.
I like problem D. And I believe I'm producing nicest solutions out of all solutions I've looked at. :) 95384262
Anyone able to provide proof as to why we only need to consider 4r consecutive celebrities ? I'm not able to figure it out as I think, as said in the editorial, any element past the 2r point will be a compatible point. What different happens at 4r ?
Thanks in advanced!
If the last celebrity you're choosing before celebrity $$$k$$$ is celebrity $$$i<k-4r$$$ then you can get a more optimal solution by also choosing celebrity $$$k-2r$$$ because you can always get both from celebrity $$$i$$$ to celebrity $$$k-2r$$$ and from celebrity $$$k-2r$$$ to celebrity $$$k$$$, so choosing $$$i<k-4r$$$ is never optimal.
the author was playing jailbreak on Roblox when he was thinking about the last problem.
I have an alternate solution to problem E: doesn't use any number theory theorem.
First of all, let's assume the number we have ends with $$$01$$$ and not $$$11$$$. If it ends with $$$11$$$, we can XOR it with its double and make it end with $$$01$$$. So we start from a number ending with $$$01$$$ : lets say we start from $$$x$$$.
form a number $$$c$$$ which is $$$x$$$ shifted left $$$k$$$ number of times, where $$$k$$$ is the bit length of $$$x$$$.
Then we XOR : $$$x+c$$$ and $$$x \oplus c$$$.
Hence we get a number $$$d$$$ which is a pure power of $$$2$$$, and is the smallest power of $$$2$$$ which is greater than $$$x$$$.
Now we will use this number $$$d$$$ to remove the highest bit of $$$x$$$: Keep multiplying $$$x$$$ by $$$2$$$, and whenever we have highest bit of $$$x$$$ and $$$d$$$ colliding, XOR them. Do it until only one bit in $$$x$$$ remains. Because $$$x$$$ ends with $$$01$$$, we get a power of 2 which is less than $$$d$$$. Use this to chop off the highest bit of $$$x$$$.
Keep chopping off the highest bit of $$$x$$$ until we get $$$1$$$.
Code