Idea and solution: flaviu2001
Think about addition in base two. Say $$$a$$$ = $$$10101$$$ and $$$b$$$ = $$$1001$$$. What your operation does is it modifies the bits in your numbers, so if the first bit in $$$a$$$ is $$$1$$$ and the first bit in $$$b$$$ is $$$1$$$ (as is the case above) you can make both $$$0$$$ by making that bit $$$1$$$ in $$$x$$$. This is actually the only way you can decrease the resulting sum, so $$$x$$$ = $$$1$$$ is an answer above.
Noticing the hint above we now deduce $$$x$$$ = $$$a$$$ & $$$b$$$ where & is bitwise $$$AND$$$. So just printing ($$$a$$$ $$$\oplus$$$ ($$$a$$$ & $$$b$$$)) + ($$$b$$$ $$$\oplus$$$ ($$$a$$$ & $$$b$$$)) works, but there's an even nicer formula. We'll leave it up to you to prove that ($$$a$$$ $$$\oplus$$$ ($$$a$$$ & $$$b$$$)) + ($$$b$$$ $$$\oplus$$$ ($$$a$$$ & $$$b$$$)) = $$$a$$$ $$$\oplus$$$ $$$b$$$, where $$$\oplus$$$ is the bitwise $$$XOR$$$ :)
1421B — Putting Bricks in the Wall
Idea: flaviu2001, solution: flaviu2001 and stefdasca
It's hard to use the two valuable switches somewhere in the middle of the matrix, a much wiser choice would be to somehow block the $$$S$$$ cell or the $$$F$$$ cell. Perhaps you can set both neighbours of $$$S$$$ to $$$1$$$ to force Roger to pick $$$1$$$.
If we pick the neighbours of $$$S$$$ to be $$$1$$$ we can make the neighbours of $$$F$$$ $$$0$$$ and there would be no way to go from $$$S$$$ to $$$F$$$. But this requires in the worst case $$$4$$$ switches, which is not good enough. Luckily, in order to get down to $$$2$$$ switches we only have to consider the other way around, making the squares neighboring $$$S$$$ become $$$0$$$ and the squares neighboring $$$F$$$ $$$1$$$. There must be a solution of the two with at most two switches and you won't get from $$$S$$$ to $$$F$$$ since you're forced to pick $$$1$$$ (or $$$0$$$) and can't get past the neighbours of $$$F$$$ which are opposite.
Idea and solution: flaviu2001
You're not allowed to just pick the whole string and append its reversed result to the front, but what's the next best thing? We're very close to the answer if we take the whole string except for a letter (so for $$$abcde$$$ we make $$$dcbabcde$$$).
The operation above which transformed $$$abcde$$$ into $$$dcbabcde$$$ is very close, if only we could've somehow append $$$e$$$ to the left. Turns out you can set that up, so from $$$abcde$$$ first append $$$d$$$ to the end, then you have $$$abcded$$$. Now apply the operation from the hint on this string and get $$$edcbabcded$$$. See why we added that $$$d$$$ first? We can now append it to the front just like we wanted!. Do the operation $$$L$$$ $$$2$$$ and the job is finished.
Yep, amazingly just printing
$$$R$$$ $$$n-1$$$
$$$L$$$ $$$n$$$
$$$L$$$ $$$2$$$
works!
Idea: flaviu2001, solution: flaviu2001 and koala_bear00
Using too many edges in the solution feels wasteful, the solution surely has some neat line as straight as possible. Perhaps we can prove only two edges are required?
Indeed two edges are required in the solution, so one approach would be picking all combinations of edges and do linear algebra so see how many times each is required (or if it's impossible).
To prove that let's suppose our target is somewhere reachable by only taking $$$C1$$$ and $$$C2$$$ (the upper right sextant, a sixth division of the plane). $$$C4$$$ and $$$C5$$$ will never be used since they contribute in the wrong direction. We can now use $$$C6$$$, $$$C1$$$, $$$C2$$$ or $$$C3$$$ for our solution. If using $$$C1$$$ and $$$C2$$$ is not optimal we can choose $$$C3$$$ or $$$C6$$$, without loss of generality we choose $$$C3$$$. $$$C6$$$ cannot be used because it simply counters $$$C3$$$. Now we either use $$$C1$$$, $$$C2$$$ or $$$C3$$$, but we can further narrow down to just two edges. If we use all three this means we use $$$C1$$$ + $$$C3$$$ which goes the same way as $$$C2$$$, and $$$C2$$$ also goes the same way as $$$C1$$$ + $$$C3$$$. So we can just not use $$$C2$$$ if $$$C1$$$ + $$$C3$$$ < $$$C2$$$, or use $$$C2$$$ instead of $$$C1$$$ + $$$C3$$$ until either of $$$C1$$$ or $$$C3$$$ doesn't appear anymore on our solution.
Idea and solution: flaviu2001
The problem gives us an array and we have to come up with an achievable sequence of pluses and minuses such that summing the numbers after applying the signs we get the largest sum. Intuitively we can probably assign $$$+$$$ to most positive numbers and — to most negative numbers somehow, but we should investigate exactly which are possible.
Before you try to find patterns you should observe that there is one case that is impossible to reach. You cannot assign alternating + and — to the array, like $$$+-+-+-+-$$$ or $$$-+-+-+-+$$$. The reason is very simple, the very first thing you do is apply the operation on two consecutive numbers and make them both $$$--$$$, and whenever you apply further operations on the both of them they remain the same sign. In the end we decided to give this in the samples but we know from testing many would miss this case.
In order to explain the solution we will add some notations:
$$$n$$$ = the length of the array.
$$$m$$$ = the number of elements we multiply by $$$-1$$$ in the solution (put — in front of them).
$$$p$$$ = the number of elements we do not multiply by $$$-1$$$ in the solution (put $$$+$$$ in front of them).
The mysterious pattern is as follows: ($$$n$$$ $$$+$$$ $$$m$$$) % $$$3$$$ = $$$1$$$
So yes, for $$$n$$$ = $$$7$$$ for example we can put $$$3$$$ minus signs anywhere, like $$$++--+-+$$$, or $$$6$$$ minus signs like $$$--+----$$$ or full plus signs $$$+++++++$$$. We can arrange the pluses and minuses however we want as long as there are $$$2$$$ consecutive equal signs and ($$$n$$$ $$$+$$$ $$$m$$$) % $$$3$$$ = $$$1$$$.
The solution now simply requires us to sort the array and multiply by $$$-1$$$ each number one by one and when ($$$n$$$ $$$+$$$ $$$m$$$) % $$$3$$$ = $$$1$$$ update the answer with the current sum. Of course there is one point where all the elements might form the forbidden $$$+-+-+-$$$ so you should check that in that case they do not, or if they do pick the next smallest number to turn into — instead of the last one. So for the sample $$$[4, -5, 9, -2, 1]$$$ you sort and get $$$[-5, -2, 1, 4, 9]$$$ and when you turn $$$-5$$$ into $$$5$$$ instead of turning $$$-2$$$ into $$$2$$$ you turn $$$1$$$ into $$$-1$$$ and the array will be $$$[5, -2, -1, 4, 9]$$$. After that undo your modification, turn $$$-2$$$ into $$$2$$$ and revert $$$-1$$$ to $$$1$$$.
The proof can be done via induction, but I will try to explain why this happens. Suppose your solution looks like $$$+--+---+$$$. What we need to do is to split into two substrings such that their negation is achievable and we are done, they will concatenate and reverse each sign. So we can split into ($$$+--$$$) and ($$$+---+$$$) and notice that their negations are ($$$-++$$$) and ($$$-+++-$$$) which are achievable (($$$n$$$ $$$+$$$ $$$m$$$) % $$$3$$$ = $$$1$$$ for both and are not alternating). We can always find such a split, start at the left-most point and see if you can split into ($$$+$$$) and ($$$--+---+$$$). You can't, the negation of ($$$+$$$) is just ($$$-$$$) which you can't have. Splitting into ($$$+-$$$) and ($$$+---+$$$) won't do either for the same reasons, but ($$$+--$$$) and ($$$+---+$$$) work, actually if the left substring starts with a $$$+$$$ the very first time the last two signs are equal is a time where we can make the split, something like ($$$+-+-++$$$) when reversed will always have ($$$n$$$ $$$+$$$ $$$m$$$) % $$$3$$$ = $$$1$$$. So now you see even clearer why the corner case $$$+-+-+$$$ exists, you can never split it into two substrings where the last two signs of the first substring are equal.
You can also see the video solutions on stefdasca's Youtube channel










Auto comment: topic has been updated by flaviu2001 (previous revision, new revision, compare).
When will the induction end for the problem E?
Why is it getting WA on pretest 4?
UPD: submission
Just submit it and wait for anwer...
I think the condition of else if(x<=0) is wrong. This condition is reached when x<=0 and x<y<0. So it should be c[4]*abs(y)+c[3]*(x-y). 95905133
I overkilled B initially by using BFS. Then I realized that it can be done by using just a couple of 'if' conditions.
Yes,it was a bit tricky. Infact i was also thinking bfs kind of stuff. But later realized that it can be solved just with a greedy aproach.
We can't avoid BFS to check if we can reach F right??
The thing is you're actually not required to check that (you don't need to optimize for minimum "c")
it is just tricky we have to just take care of 4 nodes i.e is the two neighbouring nodes of S and two neighbouring nodes of F and then we just have to make a combination like this 1. all neighbours of S are 1 and all neighbours of F are 0 2. all neighbours of S are 0 and all neighbours of F are 1
Wow so fast editorial!
C's testcase contains a major hint.
In constructive problems, the problem-setter always try to hidden the right construcion approach and even use some misleading approach in sample output, so I prefer to ignore the sample output in such problems.
However, this time it did help lol
+1
Another way to go about D is to think of the hexagonal world as a regular 2D grid, where you can move from (0,0) to six directions. [all directions except (-1,1) and (1,-1)]
Then it's just checking all the possible routes.
NB: The image is not uploading correctly for some reason. If somebody knows why, please let me know. Thanks.
Feeling depressed after seeing the solution of C and also that I thinked on it for an Hour , I got the hint part while thinking , but didn't got that we can move n-1 to n+1 .
I was a little depressed too, it took me 2 days thinking about task C to be able to solve it.
A good tip is to just look at the editorial when you think the problem uses some algorithm that you don't know. Otherwise, the best thing to do is not to look at the editorial and fight against task.
For A, even OR works
(a^(a|b))+(b^(a|b))Just use a^b as the answer.
Can anyone actually prove this?
If you're talking about proof of why XOR a^b works, then it's this way. Let's take i'th digit from both numbers (in binary). 1. If both of them are 1, then for x we put there 1 as well. This way we'll make that digit become 0 in our answer. 2. If one of them is 1, then no matter what we put there at x, that place in the answer will be 1. 3. If none of them is 1, then we need to put 0 there at x, that place in the answer will be 0. From these approaches, you can see that if digits in respective places are same, then that digit will be 0 in our answer, otherwise, it will be 1. And this is what XOR does indeed.
Another way to solve A is we can find the minimum value if we take same 2 digits like 6^6 is zero. so we can take the minimum value from a and b and put that value in x and solve the equation as it said. Simple as that.
Strong pretests for B https://www.imageupload.net/image/inkedadsiz-li.tW8IJ
Can someone please explain the dp solution in E? Thanks in advance :-)
How didn't this solution 95865345 get RE on pretests?
Edit: nvm
n is inital strings length not current
The n in (L, n) is w.r.t the new string, which is of length n+1 (after the first (R n-1)).
After solving A-D : Why did I learn algorithms ? ;ㅅ;
Wonsei your solution for problem D looks so simple. Can you please explain your idea and solution in a short? I am not understanding the editorial.
You can see here that to go from the first dot to the second dot, you can take two choices, c1 or c2+c6. so, we call n1(the cost to the right upper hexagon) minimum of those two values. You do that for all 6 directions. After that, you just go the shortest path to the destination from 0,0 using the new values.
I had a bit different solution to D.
it is easy to notice, that we need to move on diagonals, or straight line. And, number of different points we need is quite small. After drawing on piece of paper it is obvious that we need only some cominations of $$$x, y, x-y, y- x$$$. So, I added points $$$(0, x), (0, y), ...$$$ (ones on staight gorizontal line with $$$(0; 0)$$$), then $$$(x, 0), (y, 0) ... $$$ — first diagonal, and $$$(x, x), (y, y) ... $$$ on second.
We have 14 points, it`s easy to calculater distance between points on same diagonal or line. After doing so I run Floyd-Warshall on this graph, so all solution works in $$$O(14^3) = O(1)$$$;) per test case.
Code.
Did the same without running Floyd-Warshall :)
https://github.com/actium/cf/blob/master/1400/20/1421d.cpp
Great idea! I did it and 9 points is enough.
How to find the pattern of problem E in 24 minutes like kefaa2? I found it hard for me to solve this kind of problem...
Why my similar approach isn't working for C
for example:
abcd
cbabcd
cbabcd cbab
cbabcdcbab abc
printf("L %d\n",n-1); printf("R %d\n",n-2+1); printf("R %d\n",n-2+ n + 1);Don't know if the solution's correct, but maybe put "3" on the top of the answer
Oh, I had forgot to print 3. got it accepted
So fast OoO
On problem B, can anyone please tell me what does this statement really means "Waters can move from a square to any other square adjacent by a side, as long as he is still in the grid". Can Waters move from grid[i][j] to grid[i+1][j+1]?
Yes waters can move from gird[i][j] to 1 position left, or right, or top, or down, on the condition that that position should be in the grid.
In this case, 3 S10 101 01F He cannot reach to grid[n][n],then why we have to invert the squares grid[1][2] and grid[2][1]?
Yeah, that's what I had asked as a question during the contest, the reply was "there can be multiple answers"
"adjacent by side"
grid[i+1][j+1] is NOT adjacent by side to grid[i][j]
I really hope this hint/solution format of editorials becomes the norm :)
Explain this solution to me please. what is delta? what is delta_a what is delta_b?? I think a and b are the mvoes along the i and j axis. but i cant find formula for delta_a and delta_b. Thanks 95917963 stefdasca
I'm not sure why they are named that way in the code, but I recognize that it looks just like what I did. If you set up the linear equations as a matrix, delta is the determinant of the matrix and delta_a/delta_b are the matrix product of inv(A) * (x, y). When divided by delta (the determinant) they give the solutions to the linear equations (i.e. how many steps in each direction are needed).
Magical DP for E: 95899682
Many red coders have used the dp for E. Can you please explain the dp solution? Thanks :-)
Basically, the first dimension describes the number of minus signs placed modulo 3, and the other dimension is a boolean flag describing whether or not we "broke" the plus-minus-plus pattern or not. In the end, the number of minuses has to be equal to $$$2n+1$$$ modulo 3 and the flag must be on.
I have read the editorial and I understand the corner case and the proof.
But I still can not understand the way of dp transfer.
I have seen this solution: https://codeforces.com/contest/1421/submission/95897364, it is more clear in state transfer.
It seems that when we put '+' in an even position (or put '-' in an odd position), we can transfer the illegal state to the legal state.
Why we can do this?
If you have time, can you explain that? Thank you a lot!
the problem is equivalent to : assign + and — to every number , query the max sum,but "+-+-+-"is illegal and (the number of '-' + n) mod 3 =1. then the dp is obvious.
Please help! why i am getting wrong answer in Div2/C on test case 1
define ll long long int
int main() {
string s; cin>>s; ll n= s.size(); ll i,ans=0; for(i=0;i<(s.size()/2);i++) { if(s[i] == s[n-i-1]) ans++; } if(ans == n/2) { cout<<"0"<<endl; } else { cout<<"1"<<endl; cout<<"L"<<" "<<n<<endl; }}
the question clearly says only up to n-1,where n is the length of the string and u are using n.
Can someone explain what's the intuition behind the pattern in Problem E. DP aside, it seems very hard to just observe that pattern from the problem. The tutorial proves that it's right but how can we come up with something like that in the contest.
You can brute force it and look at the set of sequences of signs you get
UPD: Found the bug!
Can anyone tell me the detailed solution of Problem D. I got the part that we need to consider only two edges but how to calculate the distance after that?
find two or one direction to get to the desired hexagon. Next, try to reduce the cost of transition by adjacent hexagons (c [i] = min (c [i], c [i + 1] + c [i — 1]);). Then you find the number of steps and find the answer in long long. I found the distance just by brute force, but I'm sure that it can be better)).
I didn't think about quadrants and shortest paths in problem D
Can someone please explain a solution which involves linear algebra/matrices on problem D?
More like IfElseForces.
An interesting adaption based on B: For a given graph, what is the minimum number of invertions we need to make so that Pink Floyd can successfully go through (1,1) to (n,n)?
For example:
Then the answer should be 1. For if we invert the cell (3,4), Pink Floyd can go from (1,1) to (n,n). And it can be proved that 1 is the most optimal answer. So how to solve this?
An optimal set of inversions must either only change 0-cells to 1-cells and create a path consisting of 1-cells, or only change 1-cells to 0-cells and create a path consisting of 0-cells. So, you can run two instances of either 0-1 BFS or Dijkstra's algorithm, one to find the cost of making a path of 0-cells, and one to find the cost of making a path of 1-cells. Then the answer will be the minimum of these two values.
Thx a lot !
I am surprised that nobody I've seen did binary search for D... (The official solution seems easier, though :p)
I'm sorry if this is duplicated question. Why problems aren't rated after contests?
I can take time to set problem ratings after end of round.
I got the idea for B using 16 if-else immediately. But later spent 1 hr thinking how to implement it better. Finally ended up with an 8 if-else implementation.. Should have gone with the 16 if-else implementation itself...
How to prove the conclusion of E((n+m)%3=1) via induction?
This is clearly true for the base cases when $$$n = 1, 2, 3$$$. Now, consider a general $$$n$$$. Suppose for a moment that you have already performed the sequence of operations $$$n - 2$$$ times, and are therefore left with just two remaining elements: $$$X_1$$$ and $$$X_2$$$. Note that $$$X_1$$$ is really just the sum (with possible -1s in front) of some elements of $$$a$$$. Let $$$n_1$$$ be the number of elements in that sum, and similarly define $$$n_2$$$. (Note: $$$n$$$ = $$$n_1$$$ + $$$n_2$$$). Let $$$m_1$$$ and $$$m_2$$$ be the number of elements with -1 in front in $$$X_1$$$ and $$$X_2$$$ respectively. By our induction hypothesis, we have that
Let $$$m$$$ be the number of terms with -1 in front in our final sum after doing the operation to $$$X_1$$$ and $$$X_2$$$. Then $$$m = n_1 - m_1 + n_2 - m_2$$$.
Finally:
It's very nice to see this form of Tutorial.Thanks a lot!
MikeMirzayanov any updates when will rating get updated for previous rounds problems ?
Can someone explain why ternary search will work for D? I mean ternary search like this:
We do ternary search on distance moved along $$$y=x$$$ using C1 or C4. Then for remaining we use the Manhattan distance and use the required amount of other direction vectors. Why does this function always form a V shaped graph?
How to do it for multiple bits? Single bit proof is trivial for this :
We'll leave it up to you to prove that (a ⊕ (a & b)) + (b ⊕ (a & b)) = a ⊕ b, where ⊕ is the bitwise XOR.Upd: I got the proof. Thanks.
If you print:
At C task, you'll get ac too, it's good to think about that.
The solution for D is tiring. I'm bored of it.
D could be solved by running Simplex without making any observations :b
problem C: Palindromifier
consider substring s[2...(n-1)] as a single character. Now you get a string of length 3.
now apply
R 2
L n
L n-1
works!
example "abc" here 'b' is s[2...(n-1)
after operation 1=> abcb //here 1st b is actual b and 2nd one is reversed
after operation 2=> cbabcb // 1st b is reversed , 2nd one is actual and 3rd one is reversed
after operation 3=> bcbabcb // 1st b is actual, 2nd one is reversed, 3rd one is actual and 4th one is reversed
I struggled to solve problem D even after reading the editorial and the comments so I will try to explain it my way:
notice that all the cells on the same main diagonal have the same value y-x
notice that all the cells on the same secondary diagonal have the same value y
so to convert we do this: (d1,d2) = (y-x,y)
the numbering of the operations follows the one in the picture in the problem statement
lets prove that only 2 operations are required in the optimal solution:
as we know each operation has another opposite operation
op1 opposite of op4
op2 opposite of op5
op3 opposite of op6
that means in the final solution we can use at most 3 operations out of the six because using the operation and it's opposite has no benefit
(op1,op2,op3) or (op2,op3,op4) .... or (op6,op1,op2) and lets call each one a triplet
operations in the same triplet:
(op1,op2,op3) --> op2 = op1 + op3
(op2,op3,op4) --> op3 = op2 + op4
.......
(op6,op1,op2) --> op1 = op6 + op2
and if we do operation replacement for example (replace op2 by op1+op3 or replace op1+op3 by op2)
we end up with only 2 operations in the solution(think about it and try it on paper)
to solve the problem we need to shift the start cell (0,0) to the target cell using 2 operations and each operation might be used 0 or multiple times
so we brute force to try all pairs of operations
we notice that shifting a cell to another cell means shifting the d1 diagonal and the d2 diagonal of the first cell to match the (d1 and d2) of the target cell
each operation might be used to shift the d1 diagonal or the d2 diagonal so we also brute force 2 possibilities for each operation to try to shift on one of the diagonals each time
here is my code
For Div2D, I had the following approach
Theoretical Approach -
Consider that all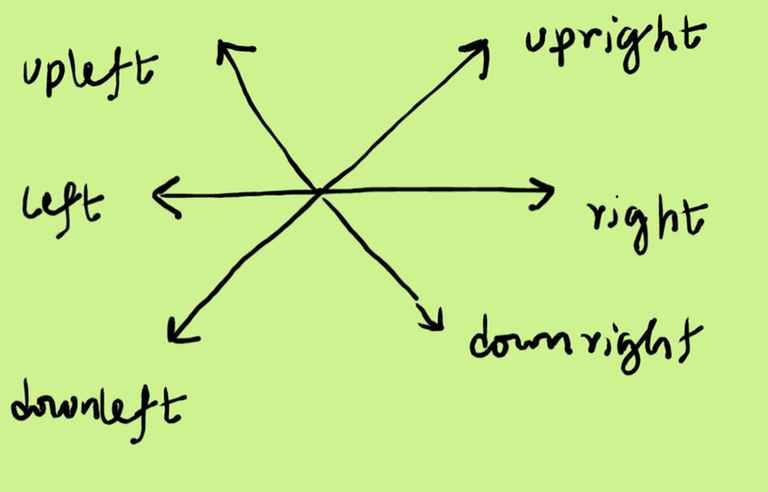 To go right, we can take — upright and downright steps. Similarly for going upright, we can take right and upleft.
To go right, we can take — upright and downright steps. Similarly for going upright, we can take right and upleft.
(X, Y)is such thatX>=0andY>=0We have the following setup —Note that we don't care for other dimensions, since
X>=0andY>=0, and other dimensions(namely left, and downleft) take us away from the target.Finally, we can add up the values —
minPossibleRight = min(right, upright + downright)andminPossibleUpright = min(upright, upleft + right)Implementation
We can rotate our coordinate axis such that right>=0 and upright >=0 For rotation, we can consider the following idea —
After rotating the coordinate axis, it becomes much more simpler.
For the problem E : "The proof can be done via induction", I didn't quite get how exactly that will work.
Assumption : For $$$n-1$$$ elements, let's say we have $$$m'$$$ minus signs. So, we will assume that $$$(n-1+m')\%3=1$$$. Now we can have the next element as a positive one or a negative one.
Say it's positive :
Then we have $$$n$$$ elements with $$$m'$$$ minuses, giving $$$(n+m'-1+1)\%3 = 2$$$ which isn't equal to 1.
Again, if it's negative :
Then we have $$$n$$$ elements with $$$m'+1$$$ minuses, giving $$$(n+m'+1+1-1)\%3 = (n-1+m'+2)\%3 = 0$$$, which again isn't equal to 1.
Obviously I am doing something wrong, but can someone point what?