Link of the problem :
https://practice.geeksforgeeks.org/contest-problem/bjorn-ironside/1/
In the hints section , they only mentioned the code of solution , which seems to involve digit dynamic programming . Can somebody explain solution to this problem or at least explain what the dp states are ? Thankyou .
Code given by them for this problem : (C++ code written in leetcode contest type format)
Code



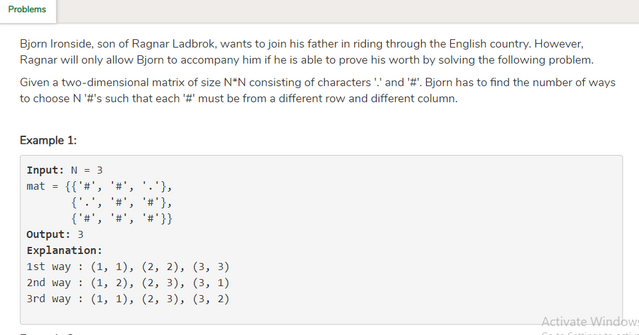








Taking some cell denies you from taking any other cell from the same row or column, so if you iterated through the rows you can take any cell that doesn't coincide with any other taken cells in the previous rows. For example, if you took the second cell from the first row, you can't take the second cell from the third row as they coincide in columns.
So the dp state will be the index of the current row and the columns which you can't take from (because you took from them in previous rows). Probably the best way to store the columns used in previous rows is a mask.
Consider that you have an integer number $$$x$$$ where the $$$i_{th}$$$ bit is on if you took from this column before, and off if you didn't. When you take from a column you just need to turn on the corresponding bit in the mask. Dealing with masks is easy, it's just weird at the beginning. You probably need to try some junk codes to get familiar with it.
So when you want to find the answer for $$$dp[i][mask]$$$, you iterate over the $$$i_{th}$$$ row and for each element $$$j$$$ such that the $$$j_{th}$$$ bit is off in $$$mask$$$ and $$$a_{i,j}$$$ equal the sharp sign, add the value $$$dp[i+1][mask\ + (1 \ll j)]$$$ to $$$dp[i][mask]$$$. The base case is reaching the $$$(n+1)_{th}$$$ row in which the answer is $$$1$$$.
Total time complexity at first sight is $$$O(n^2 \times 2^n)$$$, The number of states is $$$n\times 2^n$$$ and we iterate over the row in each state so the total is $$$O(n^2 \times 2^n)$$$. But looking closely we can notice that we will not calculate each state, let's consider the state $$$i=3$$$ and the number of bits in $$$mask$$$ is $$$5$$$. This state is unreachable. If we are in the third row the must be exactly two bits on in $$$mask$$$ (The columns of the two cells you took in the previous two rows).
So for each $$$mask$$$, there is only one valid $$$i$$$ for it. So the number of states is exactly $$$2^n$$$. Iterating on the row is $$$n$$$, so the actual time complexity is $$$O(n \times 2^n)$$$.
Thankyou so much , I familiar with masks , also I am very fine with $$$O(n^2 * 2^n)$$$ solution , but it seemed as if their code solves the problem in $$$O(n * 2^n)$$$ . Can you verify this ? Thanks again !
Sorry, I was about to sleep yesterday and I didn't calculated the actual time complexity.
I edited the comment. Read the time complexity again.