In this problem one must divide all natural numbers from 1 to n2 to groups size of n with the same sums.
Lets divide all this numbers to pairs 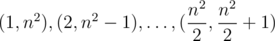 . We can to do it since n is even and therefore n2 is even too. Then we can just make n groups consists of
. We can to do it since n is even and therefore n2 is even too. Then we can just make n groups consists of  of these pairs.
of these pairs.
In this problem you must to do only what's written — you must to define does this set of points sutisfies to decribed conditions.
There are many ways to define it. For instance:
- Check if there are exactly 3 discinct x's and y's. One can put all x's to set and then get it size to find amount of distinct x's (as well as y's). Then print ``ugly'' if this amount isn't equals to 3.
- Finally we have x1, x2 и x3 as well as y1, y2 и y3. Now lets check if for every pair (xi, yj) (except (x2, y2)) such point exist in given set of points.
But I think that to read editoral of this problem is not good idea. It is better to just look at the implementation.
334C - Secrets / 333A - Secrets
Actually we are looking for longest sequence of natural number a1, a2, ..., ak, so that every number in it sequence is the power of three, sum of all numbers is more then n and if we remove any number sum will be less then n. To be precise we are looking for length of this sequence.
Consider minimal number ai = A in the sequence. All this numbers are divides to A since them all are powers of 3. And then, sum S of all this number is divides to A too. Suppose that n is divide to A too. Then, since S > n, then S - A ≥ n. And then if we remove A from sequence, sum of other number not less then n — contradist with second condition.
Well, we now that n is not divide to none element in sequence. Now lets find minimal k so that 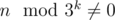 , and answer is
, and answer is 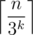 .
.
At first lets make two remarks:
- On every (vertical of horizontal) line we can put only one chip.
- If there is at least one forbidden cell on the line then we can't put chip on this line.
Follow last remark we will avoid hits chip on forbidden cells. Lets avoid ``collisions'' of chips.
Lets consider these four line: vertical lines number i and n + 1 - i and horizontal lines with the same numbers. Chips on these lines can collides together, but con't collides to another chip. Therefore we can solve the problem for these four line independently. And finally lets observe that we can put the chip on each of these lines without cillisions as well as on the picture.
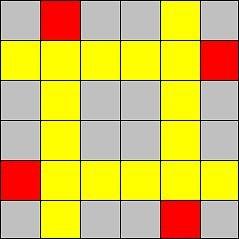
So, we can iterate all possible fours and put chip on every possible line. And don't fogot about case of two middle line in case of n is odd.
334E - Lucky Tickets / 333C - Lucky Tickets
In this problem we can find the right amount of lucky tickets.
Lets consider amount of different numbers we can get from one four-digit ticket number. It is easy to iterate all this tickets, since it amount only 104. It happened that we can get almost 60 numbers from ticket on the average.
Suppose we can get number x from ticket n. It is clearly that either x - k ≥ 0 or k - x ≥ 0. If k - x ≥ 0 we can write eight-digit ticket number who will have k - x in the first four digits and n in the last four digits. It is clearly that such ticket is k-lucky. This method allows us to get almost 600 000 lucky tickets and it is enough.
333D - Characteristics of Rectangles
In this problem we must to find maximal value of minimum of values on four intersections of two rows and two columns of table.
In another words, we are looking for maximum value of min(ai1, j1, ai1, j2, ai2, j1, ai2, j2) for all i1, i2, j1, j2 such that 1 ≤ i1, i2 ≤ n, 1 ≤ j1, j2 ≤ m, i1 ≠ i2, j1 ≠ j2. Lets us binary search of the answer. For us it we must can define is there two rows and two colums with ones on all four its intersections; in other words, integers i1, i2, j1, j2 so that ai1, j1 = ai1, j2 = ai2, j1 = ai2, j2 = 1.
Lets consider all pair of natural numbers (i1, i2) so that there exist nutural number j so that ai1, j = ai2, j = 1. Existence of two equals such pairs is equals to existence of above four numbers. But it is can be only 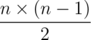 such pairs. Therefore we can make the array where we will mark pair who were meets. Lets iterate all pairs in any order until we meet repeated pair or pairs are ends. So we have solution of time
such pairs. Therefore we can make the array where we will mark pair who were meets. Lets iterate all pairs in any order until we meet repeated pair or pairs are ends. So we have solution of time 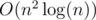 .
.
In this problem it is need to draw three circle equals together with maximum possible radius with centers in given points. In another words it is need to find triangle wich minimum side is maximal.
Unfortunately solution with bit optimize is not expected for us.
Lets call to memory two simple geometric facts. Firstly, sum of alnges of trianle is equals to 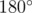 . Secondly, minimal angle is opposit to minimal side of triangle.
. Secondly, minimal angle is opposit to minimal side of triangle.
Since, at leats one side of angles of triangle not less then 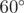 and this anlge is not least one. And side opposite to it is not least side. Therefore, if in
and this anlge is not least one. And side opposite to it is not least side. Therefore, if in 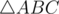
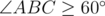 then min(|AB|, |BC|, |CA|) = min(|AB|, |BC|).
then min(|AB|, |BC|, |CA|) = min(|AB|, |BC|).
And then lets do the follows. Lets iterate apex B and for each B lets find triangle with maximal minimum of sides when B is the apex of triangle and  . For it lets sort all other points by the angle relative to B, and for each point A lets find point C most distant to B among such points that
. For it lets sort all other points by the angle relative to B, and for each point A lets find point C most distant to B among such points that  . We have to use segment tree for maximum and two pointers or binary searsh to now left and right bound of possible points C during iterating A.
. We have to use segment tree for maximum and two pointers or binary searsh to now left and right bound of possible points C during iterating A.
Finally, we have solution of time 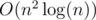 .
.











I believe it's
O(n^2 log max(a))in DYou can sort all values of our table and do binary search on this sorted sequence, which leads to O(N2·logN) algo
OK, sure.
It's O(n^2log(n^2))
O(log n^2) = O(2 log n) = O(log n)
Use binary search over a sorted list of existing numbers from the table instead of an entire range [1,10^9]. This gives you O(log(n^2)) = O(log(n)) as mentioned in the editorial.
Yes — this turned out to be crucial in accepting my bitset-bruteforce in D :)
can you tell me what is "bitset-bruteforce" solution?
You can look at my code.
how many times bitset array faster than bool array?
Around 32.
Using bitset in C++ STL, we can pass D and E :(
please can you write some details for these solutions
If we want to pass E An algorithm O(n^3):for circle i,j,k,we can check it and get answer. We know all distance of every pair,sort it If dis(i,j) is answer,dis(i,k)<=dis(i,j),mark[i][j]=true.I try each answer and they are sorted,so when I try dis(i,j),if mark[i][k]=true and mark[j][k]=true,we can print dis(i,j) If mark[i] is a bitset,and the k is exist,then (mark[i]&mark[j]).any() is not 0. We have an algorithm,O(n^3/32),and it can pass E Sorry for my English.In fact,my English is so poor that my teacher criticized me. T_T
Another way to solve E: first, binary search on the result r (complexity factor: ), then fix one vertex A of the triangle (complexity factor: n). We want to find two other vertices B, C such that all three distances are ≥ 2r. Let's consider only the set S of those vertices that are farther than 2r from A. Now obviously, there are two vertices
), then fix one vertex A of the triangle (complexity factor: n). We want to find two other vertices B, C such that all three distances are ≥ 2r. Let's consider only the set S of those vertices that are farther than 2r from A. Now obviously, there are two vertices 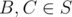 with dist(B, C) ≥ 2r if and only if the maximum distance of two points in S is ≥ 2r. And this can be found using convex hull and rotating calipers (complexity factor:
with dist(B, C) ≥ 2r if and only if the maximum distance of two points in S is ≥ 2r. And this can be found using convex hull and rotating calipers (complexity factor: 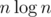 ).
).
(Actually, we need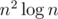 , not
, not 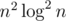 . But notice that the
. But notice that the 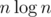 in convex hull comes from sorting the points. We can do that just once after reading the input. Then, after filtering out the too-close vertices, the list is still sorted.)
in convex hull comes from sorting the points. We can do that just once after reading the input. Then, after filtering out the too-close vertices, the list is still sorted.)
Very nice solution.
I tried to implement it on my own. I just want to add, that it must be implement very carefully. It's important to avoid using double arithmetic, because you can recieve TLE. But with long longs, it's fast enough.
I changed one line in your solution (4195968) and it became two times faster :)
Of course, I should realize, that I don't need long longs. And arithmetic on ints is even quicker. Thank you, for your tip :)
for problem Div1 D ,How this submission with complexity O(N^3) passed? 4183580
also how functions fastMax and fastMin work?
it is really surprising, i replaced min/max by fastMin/fastMax and it got accepted!!! (time taken = 2.9s)
-1 & (x ^ y) = (x ^ y).
(x ^ y) ^ y = x.
0 & (x ^ y) = 0.
0 ^ y = y.
deleted
Wow, nice :D. How many times approximately is this fastMin faster than the usual one?
Besides, I think that finding such formulas for min and max is much harder than that problem :P.
How does operators
<<and>>work for negative numbers?Implementation defined as I remember.
Usually it's multiplication/division by 2 (rounding down)
I did some tests.
rep(i, 1000000000) a = std::max(1000, -1000);takes 4148.88 ms
rep(i, 1000000000) a = fastmax(1000, -1000);takes 3738.1 ms
It's near 10% faster; not that great. Asymptotic running time is still the big deal. Having this trick under your sleeve is nice though.
PS: With any optimization flag they both take 0 ms :P
you can't test in this way. because iterating from 1 to 1000000000 the jump operations and add operations spent most of the time.
try like this: rep(i, 1000000) { a = fastmax(1000, -1000); a = fastmax(1000, -1000); a = fastmax(1000, -1000); a = fastmax(1000, -1000); ... ... 1000 times ... a = fastmax(1000, -1000); }
Am I the only one who got accepted without any fastmax and fastmin ? 25100623 My O(n ^ 3) solution passed comfortably in 2 seconds
334C — SECRETS
for n=8 ... can not the buyer just give 9 mark coin ??
May be, he haven't this coin?
I'm surely missing something here .. , because I don't get the point of buyer not having 9 mark coin (as it is given that buyers have all the denominations that are divisble by 3), pls hlp!!! this question is really confusing me
yes, he can, but this is not the maximum number of coins. the maximum number is 3 (3 mark coin);
pls explain this -> For each such combination calculate the minimum number of coins that can bring the buyer at least n marks
{ for n=8 :
9-> 3+3+3 (it can not be further reduced) or 9
10->not possible
12-> 3+3+3+3 reduced to 3+9 ... } Is above explanation of mine is correct??
No, it is not correct. the problem statement says " Among all combinations choose the maximum of the minimum number of coins "
Sorry for posting here so late: The combination are: For 9: it's 1 (denomination 9) For 10: it's 2 (9+1) For 12: it's 2 (9+3) . . Till which mark do we need to iterate and for 8 how the answer is 3. Kindly clarify them. TIA.
I can't understand D's solution. Can anybody explain more clearly?
Nobody care
Care cái sỏi
I am finding it difficult to understand the solution of D too.
We binary search for the answer. Note that the answer is one of a[i][j] only. So for a fixed k, we want to find whether there exists a rectangle all 4 of whose corner numbers are >= k. So to do this for a fixed k, define a boolean array b[n][m] where b[i][j] = 1 if a[i][j] >= k and 0 otherwise.
Now the problem is reduced to finding a rectangle in b[n][m] all of whose corner numbers are 1. For each pair of rows (r1, r2), if there exists a j such that b[r1][j] = b[r2][j] = 1 then we say that (r1, r2) is a "good" pair. Note that there are atmost nC2 good pairs. Now we iterate over all pairs of 1's that are in the same column, and mark the pair of corresponding rows as good (in a map). If the pair is already present in the map, "k" can be obtained and we are done. Keep iterating in any random order, till you encounter a repeated good pair of rows. If you exhaust all vertical pairs of 1's and still don't have a repeated good pair of rows, then "k" cannot be obtained and we are done again.
Won't iterating over all pairs of 1s that are in the same column be O(n*n*n)?
Store an array good[n][m] initialized to 0.
Now, for each row: Store positions of all 1s in a vector
For each pair (i,j) in the vector:
If good[i][j] is 0, set good[i][j] to 1.
If good[i][j] is 1, then that means there exists a column in which row i and row j are set to 1. And in the current column, row i and row i have values 1 as well. Therefore, we have our answer and stop here.
So, initially all of good[n][m] is 0. At each step, you are changing a good[i][j] to 1. You can only do that N*N times. When you find you are trying to change a good[i][j] that is already 1, you stop.
You are so cute when rehearsing the content of this post =)
Is that sarcasm?
hm, and judging by amount of downvotes few understood it...
So you mean good[m][m] not good[n][m]... right?
That one was confusing me.
Thank you guys, now I understand the solution. The tutorial says that we must find a rectangle with 4 of its cornors are 1, and I really don't know what the heck 1 is =))
for problem Div1 D ,will it take o(n) to find j so that ai1,j= ai2,j=1? when we meet repeated pair and return(4183297),how to compute the overall solution of time,why it's o(n^2 log(n))?
Though it seems has O(N^3) iterations to find the two pairs, in every iteration it will find a new good pair(record it in a 2-d array good) or a repeated pair(thus find the two pairs and return). There are only O(N^2) states in 2-d array good, So it has at most O(N^2) iterations overall. Combined with binary search of answer, it gives O(N^2)log(n) algorithm. Codes 4192623
I am very annoyed by the bad translation !
Can someone please explain the logic behind Div2 C problem ? I am not able to understand the tutorial.
Ok. We see from statement, that we are looking for the longest possible sequence a1, a2... ak with these properties:
all numbers ai are powers of three -- we only know coins with these values
sum S of these numbers is larger than n -- we must pay larger amount of marks, because buyer doesn't have exact amount
Now denote minimal ai as A. Other ai are larger or equal, so these number are multiples of A. If S is sum of all elements ai and each element is divided by A, than S is also diveded by A.
Now let's consider, that n is diveded by A. We know, that S is multiple of A, n is multiple of A and S is larger than n. So S - n ≥ A which means, that n ≥ S - A. But this is contradiction with last property of our sequence. So n cannot be divided by minimal ai in our sequence.
Last thing is, that if we want the longest sequence, all numbers should be equal. This is pretty obvious, because if A is minimal element, than any larger element is multiple of A and can be distributed to more A elements.
Now you can iterate through all k such as 3k ≤ n. If 3k doesn't divided n, than you can obtain answer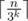 . And the biggest such number is final answer. If n is power of three, then answer is 1.
. And the biggest such number is final answer. If n is power of three, then answer is 1.
My code here: 4175901
I hope, this will help.
Thanks for a great explanation :)
I've got similar solution for problem Div1-D, but I don't use binary search. Complexity of my solution is still , but in my opinion it's easier to implement.
, but in my opinion it's easier to implement.
So the main idea is the same. Consider pair of columns (c1, c2). Two such pairs in different rows (r1, r2) creates one possible solution -- rectangle with characteristic min(ar1, c1, ar2, c1, ar1, c2, ar2, c2). And we want the largest characteristic.
We sort all numbers in rectangle from the biggest to the smallest. Now we will add these number in this order. When we add element ai, j it creates pair of columns with every element on row i, which are greater (or equal and were added before). So we store these elements in vector (one for each row) and iterate them. During this we count, how many times we see which pair of columns. When we see some pair the second time, we have possible solution and because we add elements from biggest one, it's also the largest rectangle. So value of the last added element is answer.
Time complexity: we need time time for sort all numbers. Then we add each pair of columns at most once, so the complexity is O(n2). Overall it's
time for sort all numbers. Then we add each pair of columns at most once, so the complexity is O(n2). Overall it's  .
.
Here is my code: 4183958
I'm sorry but after reading this editorial I'd a feeling like this
in my opinion:
RIP codeforces editorials
Learn a lot from your solution of 333E - Summer Earnings. thx. :D
In E, we can avoid implementing segment tree and use a deque to maintain maximum on interval that is being held by two pointers (check this submission 4213091).