Idea: adedalic
Tutorial
Tutorial is loading...
Solution (Ne0n25)
for i in range(int(input())):
a, b, c = map(int, input().split())
if (a + b + c) % 9 != 0:
print("NO")
else:
print("YES" if min(a, b, c) >= (a + b + c) // 9 else "NO")
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (Ne0n25)
for t in range(int(input())):
n = int(input())
a = list(map(int, input().split()))
s = sum(a)
cur = [0, 0]
for i in range(n):
cur[i % 2] += a[i] - 1
for j in range(2):
if 2 * cur[j] > s:
continue
for i in range(n):
if i % 2 == j:
a[i] = 1
break
print(*a)
Idea: KAN
Tutorial
Tutorial is loading...
Solution (pikmike)
def inside(l, r, x):
return min(l, r) <= x <= max(l, r)
def sg(x):
return -1 if x < 0 else int(x > 0)
for _ in range(int(input())):
n = int(input())
qs = []
for i in range(n):
qs.append(list(map(int, input().split())))
qs.append([4*10**9, 0])
ans = 0
pos, dr, lft = 0, 0, 0
for i in range(n):
t, x = qs[i]
tn = qs[i + 1][0]
if lft == 0:
lft = abs(pos - x)
dr = sg(x - pos)
tmp = min(lft, tn - t)
if inside(pos, pos + dr * tmp, x):
ans += 1
pos += dr * tmp
lft -= tmp
print(ans)
Idea: adedalic
Tutorial
Tutorial is loading...
Solution 1 (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
const int INF = int(1e9);
int n;
vector<int> b;
inline bool read() {
if(!(cin >> n))
return false;
b.resize(n);
fore (i, 0, n)
cin >> b[i];
return true;
}
bool ok(const vector<int> &a, const vector<int> &b, int cnt) {
fore (i, 0, cnt) {
if (a[i] >= b[sz(b) - cnt + i])
return false;
}
return true;
}
inline void solve() {
vector<int> nb;
fore (i, 1, 2 * n + 1) {
if (!binary_search(b.begin(), b.end(), i))
nb.push_back(i);
}
int mx[2] = {-1, -1};
fore (k, 0, 2) {
int lf = 0, rg = n + 1;
while (rg - lf > 1) {
int mid = (lf + rg) / 2;
if (ok(b, nb, mid))
lf = mid;
else
rg = mid;
}
mx[k] = lf;
if (!ok(nb, b, n - lf)) {
cout << 0 << endl;
return;
}
swap(b, nb);
}
assert(n - mx[1] <= mx[0]);
cout << mx[0] - (n - mx[1]) + 1 << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
int t; cin >> t;
while(t--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Solution 2 (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
const int INF = int(1e9);
int n;
vector<int> b;
inline bool read() {
if(!(cin >> n))
return false;
b.resize(n);
fore (i, 0, n)
cin >> b[i];
return true;
}
int getMax(const vector<int> &a, const vector<int> &b) {
int uk = 0;
fore (i, 0, sz(a)) {
while (uk < sz(b) && b[uk] < a[i])
uk++;
if (uk >= sz(b))
return i;
uk++;
}
return sz(a);
}
inline void solve() {
vector<int> nb;
fore (i, 1, 2 * n + 1) {
if (!binary_search(b.begin(), b.end(), i))
nb.push_back(i);
}
int mxX = getMax(b, nb);
int mnX = n - getMax(nb, b);
cout << mxX - mnX + 1 << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
int t; cin >> t;
while(t--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (pikmike)
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for(int i = 0; i < int(n); i++)
vector<vector<int>> g, h, ng;
vector<int> rk, p;
int getp(int a){
return a == p[a] ? a : p[a] = getp(p[a]);
}
void unite(int a, int b){
a = getp(a), b = getp(b);
if (a == b) return;
if (rk[a] < rk[b]) swap(a, b);
rk[a] += rk[b];
p[b] = a;
}
vector<vector<int>> comp;
vector<int> ord;
vector<int> used;
bool fl;
void ts(int v, const vector<vector<int>> &g){
used[v] = 1;
for (int u : g[v]){
if (used[u] == 0)
ts(u, g);
else if (used[u] == 1)
fl = false;
if (!fl) return;
}
ord.push_back(v);
used[v] = 2;
}
bool topsort(const vector<vector<int>> &g){
int n = g.size();
used.assign(n, 0);
ord.clear();
fl = true;
forn(i, n) if (!used[i]){
ts(i, g);
if (!fl) return false;
}
reverse(ord.begin(), ord.end());
return true;
}
vector<int> pos;
bool dfs(int v){
for (int u : g[v]){
if (pos[u] < pos[v])
return false;
if (!dfs(u))
return false;
}
return true;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
g.resize(n);
h.resize(n);
ng.resize(n);
int rt = -1;
forn(i, n){
int p;
scanf("%d", &p);
--p;
if (p == -1)
rt = i;
else
g[p].push_back(i);
}
rk.assign(n, 1);
p.resize(n);
iota(p.begin(), p.end(), 0);
forn(i, m){
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
h[v].push_back(u);
unite(v, u);
}
if (!topsort(h)){
puts("0");
return 0;
}
auto ord1 = ord;
vector<int> pos1(n);
forn(i, n) pos1[ord1[i]] = i;
forn(v, n) for (int u : g[v]) if (getp(v) != getp(u))
ng[getp(v)].push_back(getp(u));
if (!topsort(ng)){
puts("0");
return 0;
}
comp.resize(n);
forn(i, n) comp[getp(i)].push_back(i);
vector<int> fin;
for (int it : ord){
sort(comp[it].begin(), comp[it].end(), [&](int v, int u){ return pos1[v] < pos1[u]; });
for (int v : comp[it])
fin.push_back(v);
}
pos.resize(n);
forn(i, n) pos[fin[i]] = i;
if (!dfs(rt)){
puts("0");
return 0;
}
for (int v : fin)
printf("%d ", v + 1);
puts("");
}
Idea: Neon
Tutorial
Tutorial is loading...
Solution (Ne0n25)
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;
const int N = 22;
int dp[2][1 << N];
int val[2 * N];
int main() {
int n, x, y;
scanf("%d%d%d", &n, &x, &y);
int k = x + y;
int m = max(x, y);
int FULL = (1 << m) - 1;
for (int i = 0; i < k; ++i)
val[i] = n / k + (i < n % k);
for (int mask = 0; mask < (1 << m); ++mask)
dp[0][mask] = -INF;
dp[0][0] = 0;
for (int i = 0; i < k; ++i) {
for (int mask = 0; mask < (1 << m); ++mask)
dp[1][mask] = -INF;
for (int mask = 0; mask < (1 << m); ++mask) {
if (dp[0][mask] == -INF)
continue;
int nmask = (mask << 1) & FULL;
dp[1][nmask] = max(dp[1][nmask], dp[0][mask]);
if (((mask >> (x - 1)) & 1) | ((mask >> (y - 1)) & 1))
continue;
nmask |= 1;
dp[1][nmask] = max(dp[1][nmask], dp[0][mask] + val[i]);
}
swap(dp[0], dp[1]);
}
int ans = 0;
for (int mask = 0; mask < (1 << m); ++mask)
ans = max(ans, dp[0][mask]);
printf("%d\n", ans);
}










great tutorial and congratulations on completing century of educational rounds... wow
another approach for B is that we can round DOWN the value at each index to the closest power of 2. Then just print the array. Although it was a tougher contest than usual, as far as i know.
2∑i=1n|ai−bi|≤S How is this condition satisfied in the solution you mentioned?
When you round DOWN any number to the nearest power of 2, new number will still be greater than or equal to half of the current value. EXAMPLES:
32 round DOWN TO 32 itself(nearest power of 2).
30 round DOWN TO 16 (nearest power of 2).
in above example it is clearly seen or observed that new number will still be greater than or equal to half of the current value.... THAT IS IT IS MAXIMUMLY REDUCED TO HALF OF INITIAL VALUE.
NOW ARRAY EXAMPLE: A1 A2 A3 A4
transformed to B1 B2 B3 B4
WHERE EVERY Bi IS EQUAL TO NEAREST POWER OF 2.
(A1+A2+A3+A4)=S
SO (A1-B1)<=(A1/2)
SO (A2-B2)<=(A2/2)
SO (A3-B3)<=(A3/2)
SO (A4-B4)<=(A4/2)
NOW DOING SUM ON BOTH SIDES:
THUS SIGMA(Ai-Bi)<= ((A1/2)+(A2/2)+(A3/2)+(A4/2))
HENCE PROVED
another approach for B is 2^k
Let x[i] = log2(a[i])
then b[i] = 2^x[i]. It can be prove that sum of all 2*|a[i] — b[i]| always <= S
This problem can be extend to k*|a[i] — b[i]| <= S. It will be so funny XD
Proof: At first, if each b[i] is a power of 2 the first condition will be done. Let's prove the second condition will be done too. It means that b[i] >= ceil(a[i] / 2) for each i. If b[i] is equal to 2^k, where k = floor(log2(a[i])) the second condition will be done as well. Let's say x = a[i] = 5. It's 101 in binary representation. y = b[i] = 4. It's 100 in binary representation. Then, x / 2 = 5 / 2 = 101 >> 1 = 010 = 2. After the operation the highest bit in x / 2 will be equal to 0, but at the same time it's equal to 1 in y. Hence, y > x / 2. We have proved it.
I'd love to see a clean implementation of problem 2C in C++, if possible. Can someone point me in the right direction here?
Maybe you can have a look at my code. It is easy to understand I think.
Thanks a lot. I've spent half an hour thinking about an algorithm which has an O(nlogn) time complexity but I didn't get accepted. The solution is really an ingenious solution. Thanks very much!
(P.S.: I'm a foreigner, if I made spelling mistakes, please forgive me. Thank you.)
I still can't understand the code, please explain the last condition if possible
In this solution,
landrare the begin time and the end time of the last command isn't ignored, andfromandtoare the begin position and the end position of the command.If
t[i]>=r, the last command that isn't ignored changes intoi, so update the four variables and check if it is successful.Otherwise, calculate the position range $$$[l_{now},r_{now}]$$$ that robot stays in the time range $$$[t_i,t_{i+1}]$$$. To do this, we first determine the direction of the last command with
(to-from)/(r-l). ($$$-1$$$ means left and $$$1$$$ means right) Second, at time momentt[i], robot moved fort[i]-lseconds, and at time momentt[i+1], robot moved formin(t[i+1]-l,r-l)seconds. (the robot may stop before the time momentt[i+1]so don't forget themin) Of course, ifl_now>r_now, you need to swap them. Finally, you can just check if it is successful by checking ifx[i]is in the range $$$[l_{now},r_{now}]$$$.Can anybody say other approaches of problem B?
Yes. For example, we can print 2^k, where k = floor(log2(Ai)) for each i.
My submission: https://codeforces.com/contest/1463/submission/101614243
Proof: At first, if each b[i] is a power of 2 the first condition will be done. Let's prove the second condition will be done too. It means that b[i] >= ceil(a[i] / 2) for each i. If b[i] is equal to 2^k, where k = floor(log2(a[i])) the second condition will be done as well. Let's say x = a[i] = 5. It's 101 in binary representation. y = b[i] = 4. It's 100 in binary representation. Then, x / 2 = 5 / 2 = 101 >> 1 = 010 = 2. After the operation the highest bit in x / 2 will be equal to 0, but at the same time it's equal to 1 in y. Hence, y > x / 2. We have proved it.
As you pointed out, getting the nearest $$$2^k \leq x$$$ can be done by only keeping the most significant bit (MST) of $$$x$$$. Therefore, if we could get the number of trailing bits from the MST, we would have $$$k$$$. You can implement this by yourself, but you can also make use of GCC compiler built-in function
__builtin_clz()which counts the number of leading 0-bits from the MST (refer to here, I think it's a very useful post). Then, considering anintvariable type has 32 bits, $$$k =$$$31-__builtin_clz(x)(subtraction is from 31 as otherwise we would count the MST, too). Having this, calculating powers of two it's easier and faster using the shift operator (<<), as $$$2^k =$$$1<<k, that is to say, bitwise it's just shifting the number 1, $$$k$$$ times to the left.Here is my submission: 101681555. I wanted to show this variation of the solution as it ends up pretty nice and short, and it also may be useful to know when working with powers of two.
Good job! Thank you a lot!
Here's a different solution which I think is a little more simple, (my code 101560737)
You can alternate between taking the number in A and taking 1. So your array B The intuition is that will look like this: B = [ a, 1, a, 1, a ... ]
The differences will be, A — B = [0, a-1, 0, a-1, 0 ....]
although it may happen that the difference is bigger if you take the zeros when a_i is a big number.
However we can prove that by taking zeros on either the even indices or the negative indices, we get a sum of at most S/2 (S being the sum of all elements in A)
[0, a-1, 0, a-1, 0, a-1 ... ] + [a-1, 0, a-1, 0, a-1, 0 ... ] = [a-1, a-1, a-1, a-1, a-1, a-1 ...]
The sum of all the differences will be: S-n (where n is the number of elements in A)
This means that on average, if we use this method we will get a sum of differences of (S-n)/2. To guarantee a correct answer we can use this method with even indices and odd indices, calculate our score, and choose the one which is lower.
Hi Everyone !! Me and my friends tried to make the video editorials for this round, Please give a look and provide your valuable feedback : https://codeforces.com/blog/entry/85706
very nice video editorials !!
Now I want you to answer a question which is probably the most asked question in history of codeforces.
How to become an orange coder ? What exact path or strategy we can follow ?
Although many coders have answered such questions but it is always beneficial to listen 1 more time.
Practice
I may do a lot of practice but that practice won't yield much if I don't choose a correct strategy or a path .
I am practicing a lot but i am improving less. What may be the problem? Can someone tell. Everyone is welcomed to showcase their views.
You should start practicing problems of difficulty 1600-1800 and strengthen your graphs and DP.
Thank you
Always practice the problems whose difficulties are a bit higher than your present level. Try to think it up by yourself and do not read the tutorial unless you are sure you can't make it.
Suggestion: It would be good to find the find the links of the problem and solution in the you tube description area.
Yes, we will make sure that.
There's another O(n) solution for D. This is my code.
But I don't know how to explain this works... English is too hard
tidy solution! Can someone explain this approach?
To explain more clearly, we define that $$$a=\{x \; | 1 \le x \le 2n, \forall \; 1 \le i \le n, x \neq b_i \}$$$. In other words, $$$a=\{1,2,\cdots,2n\} \setminus b$$$. Then we need to solve the problem that we arrange $$$a$$$ in some order to make there are exactly $$$x$$$ pairs $$$(a_i,b_i)$$$ such that $$$b_i<a_i$$$.
First, it is clear that $$$x \in [l,r]$$$ and $$$0 \le l \le r \le n$$$ so we need to determine $$$l$$$ and $$$r$$$. If we do it, the answer should be $$$r-l+1$$$.
What does this approach do? It assigns $$$A_i$$$ the value of $$$1$$$ if $$$i \in b$$$ and the value of $$$-1$$$ if $$$i \in a$$$. Then it makes $$$A_i=\sum_{j=1}^i A_j$$$ and $$$maxx=\max\{A_i\}$$$ and $$$minn=\min\{A_i\}$$$. Finally, it prints $$$n+1-maxx-(-minn)$$$. (it is easy to discover that $$$maxx \ge 0$$$ and $$$minn \le 0$$$ because $$$A_{2n}$$$ is always $$$0$$$ )
Assume that $$$A_p=maxx$$$. The number of numbers from $$$b$$$ is $$$maxx$$$ greater than the number of numbers from $$$a$$$ which aren't greater than $$$p$$$. So there are at least $$$maxx$$$ numbers from $$$b$$$ which are not greater than $$$p$$$ must match to some numbers from $$$a$$$ which are greater than $$$p$$$. That's why $$$l=maxx$$$.
Similarly, assume that $$$A_q=minn$$$. The number of numbers from $$$a$$$ is $$$-minn$$$ greater than the number of numbers from $$$b$$$ which aren't greater than $$$q$$$. So there are at least $$$-minn$$$ numbers from $$$b$$$ which are greater than $$$q$$$ must match to some numbers from $$$a$$$ which are not greater than $$$q$$$. That's why $$$r=n-(-minn)$$$.
That's why the answer is just $$$r-l+1=n-(-minn)-maxx+1$$$.
Wow! Thanks for the nice explanation.
Can anybody explain the solution of problem E?
Consider the prerequisite edges marked as 0 and special pairs as edges marked as 1.
if a single vertex has more than one edges marked as 1 outgoing or incoming than it's not possible to find an ordering. Moreover, the graph should not contain any cycle.
After checking this we can first group all the edges marked as 1 they will form a simple path, compress all the vertices to a single vertex and assign it as a parent of all vertices. Also keep the ordering of vertices for that component.
Now add the edges marked as 0 in the new graph between parent of vertices, if both have different parent add the edge else we can ignore that cause we already checked for cycle. After this topsort the graph, if it is not possible than answer is zero else find the topsorted list will give a valid ordering. Print them by iterating through every vertex list that we found in the compression stage. my code
CODE A Solution is wrong. In Last line it will be " print("YES" if min(a, b, c) >= (a + b + c) // 7 else "NO") "
include<bits/stdc++.h>
using namespace std; int main(){ long long int t,a,b,c; cin>>t; while(t--){ cin>>a>>b>>c; long long int sum=a+b+c; long long int d=sum/7; if(((sum%9)==0) & (a>=d) & (b>=d) & (c>=d)) cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0; }
d should be sum/9 and also you have to use '&&' instead of '&'
sorry,my bad,'&' will also work
Can someone please explain ecnerwala solved the F problem 101602047 using
gcd?It turns out that, given the lemma from the editorial (there exists an optimal string with period $$$x+y$$$), this problem can be solved in $$$O(x+y)$$$ time.
First, if $$$g = \gcd(x,y) \ne 1$$$, we can split the problem up by mod $$$g$$$, because all edges connect two things that are separated by $$$x$$$ or $$$y$$$, which are multiples of $$$g$$$. Thus, we can assume $$$\gcd(x,y) = 1$$$.
The key thing to observe is that all edges span $$$\pm x$$$ modulo $$$x+y$$$. Because of the lemma, we can merge all nodes with the same residue mod $$$x+y$$$ to get $$$x+y$$$ super-nodes. Furthermore, because the edges are exactly the changes by $$$\pm x$$$ mod $$$x+y$$$, and we assumed $$$\gcd(x,y) = 1$$$, these supernodes form exactly 1 complete cycle. Then, instead of doing the DP in $$$1 \ldots x+y$$$ order, we can use the order of this cycle ($$$x, 2x, 3x, \ldots \pmod{x+y}$$$). This means our DP only needs to track whether we took the first element and whether we took the latest, so there are only $$$4(x+y)$$$ states.
what are edges here?
Consider the graph where two vertices $$$a,b$$$ have an edge if $$$|a-b| \in \{x,y\}$$$, so that this problem is about finding maximum independent set.
Am I the only person who didn't like problem C?
Disappointedly not a decent explanation. Where understanding is so tough, there solving is just a fun
Can anybody help me in my submission of C submission. Thanks in advance.
Consider the following test case: Your first command on $$$t = 1$$$ is to go to $$$x = 10^9-1$$$. It will arrive on $$$t = 10^9$$$. Then the second and last command is on $$$t = 10^9$$$ (which the robot won't ignore as it's not moving anymore), to go to $$$x = -10^9$$$. You can see it will take $$$\left|(10^9-1)-(-10^9)\right| = 2\cdot10^9-1$$$ units of time to get there. Therefore, it will arrive at $$$t = 3\cdot10^9-1$$$.
Both commands are successful, while your code will only tell the first one is successful, as your variable
mmmwhich you add at the end of the list of commands in what it seems to be a "dummy" element, is only equal to $$$10^9+5$$$, restricting your time range and therefore calculating incorrectly the range of positions where the robot would pass, and by so not counting the last command as successful. Increasing that value to $$$3\cdot10^9$$$ should fix the issue, but of course by doing that you may have to be careful and work withlong longvariable types.Ouch.
Thanks a lot man, feel so stupid should have set it to 1e10 or something. Also int is actually long long in my snippet and main function returns int32_t. Thanks again.
Another approach to B for those who need: At first, if each b[i] is a power of 2 the first condition will be done. Let's prove the second condition will be done too. It means that b[i] >= ceil(a[i] / 2) for each i. If b[i] is equal to 2^k, where k = floor(log2(a[i])) the second condition will be done as well. Let's say x = a[i] = 5. It's 101 in binary representation. y = b[i] = 4. It's 100 in binary representation. Then, x / 2 = 5 / 2 = 101 >> 1 = 010 = 2. After the operation the highest bit in x / 2 will be equal to 0, but at the same time it's equal to 1 in y. Hence, y > x / 2. We have proved it.
Can someone tell approach of problem D?
does anyone else feels that Problem: C could have been more clearly explained ?
Can you tell me how do you understand it? I've reread the last paragraph of the legend a hundred times and still have no idea how can you interpret it other than the intended way...
We were getting questions about it during the contest, I was answering "The robot should visit $$$x_i$$$ at some moment between $$$t_i$$$ and $$$t_{i+1}$$$" and the people seemed to be getting it and not returning with more questions, but I literally see no difference between the statement and that...
Why do we not consider the first command as successful command?
Why do you think it always satisfies the condition for being successful?
We start at t0 and reach our destination at t1 seconds.
You start at $$$t_1$$$ and should reach it before $$$t_2$$$.
So u are saying that when our robot starts at t1 sec it should reach x1 before t2 seconds.
But in the problem statement we are have to reach our our destination( in this command x1) at t2 seconds.(As per my understanding correct me if I'm wrong), As both bounds are inclusive.
You call the command i successful, if there is a time moment in the range [ti,ti+1] (i. e. after you give this command and before you give another one, both bounds inclusive; we consider tn+1=+∞) when the robot is at point xi.Yes but you are moving 1 unit per second, have you noticed that?
Can You Expain the answer with this test case. `6
3 10
5 5
8 0
12 -4
14 -7
19 -5 `
dist : [0,0,0,0,1,2,3,4,5,6,7, 8, 9, 10]
time :[0,1,2,3,4,5,6,7,8,9,10,11,12,13]
Can you explain it? I still have no clue how can you understand that problem so that the answers are not complete nonsense but still wrong.
at t = 3 sec we are at x = 0, t = 7 we reach x = 4, similarly we reach x = 10 at exacty t = 13 seconds, our time interval was [3,13], x1 was 10. t = 13 is the time before i give new command.
[ti,ti+1] (i. e. after you give this command and before you give another one, both bounds inclusive; we consider tn+1=+∞)Acoording to above statement.
Ah, I see. You should not ignore $$$t_i$$$ for the commands that are ignored. $$$t_{i+1}$$$ is literally the time the $$$(i+1)$$$-th command gets sent (not necessarily executed).
DELETED
EDIT : understood the question in the wrong way
I think there is a O(n) solution for problem E. I not sure about it. But it pass the test.
It's true. I think it's not necessary to find the order of the vertices inside each component by sorting, as you can just have for each lecture, the previous and next lecture in each of the components of special pairs, and reconstruct in linear time from each component after the topsort. Then you would just check if no lecture which should be a prerequisite is given after the one you're checking in the ordering, and thereby determine if no answer exists or that it does and you have to print the solution.
At least with that I could also pass the tests with an almost $$$\mathcal{O}\left(n\right)$$$ solution (just used a set for counting components, but can easily be replaced with something that also works in linear time... 101592299).
We can also do it without using binary search and checking for each x. I found out if we construct an array C, whose entry is (indice of upper bound of b[i] in nb) — i. Then for each x the condition becomes that - The maximum of C from [0, x — 1] <= (n — x) and minimum of C from [x, n — 1] > -x . We count such valid x. Accepted Code
Practice! Happy New Year!
.
The statement clarifies: " i. e. after some enhanced shot, the health points of each of the monsters should become equal to $$$0$$$ for the first time ".
In your test case and the way you've shown of killing the monsters, you can see that the second monster gets killed (health points drops to $$$0$$$) after the 7th movement while the others haven't yet. You can prove that there's no way of fulfilling this condition in that test case.
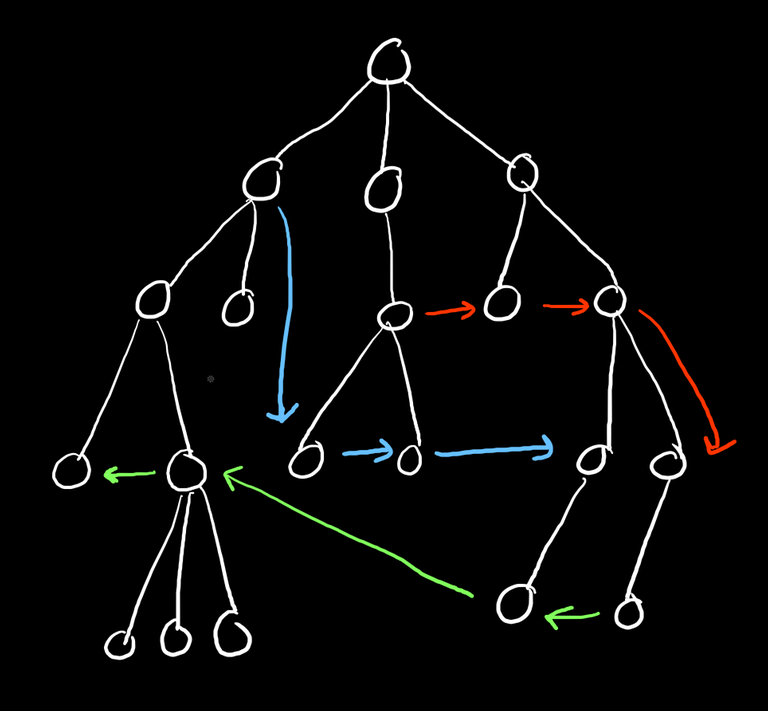
For problem E, if you're having trouble understanding why the algorithm always works, you can see that, if you firstly build the tree, and then draw the paths created by the special edges, none of these paths should cross each other, ie if some vertex in special path A is an ancestor of some vertex in special path B, then no vertice of B can be an ancestor of any vertex in special path A. (there are a couple more conditions about there being no special edges to an ancestor or to an indirect child)
By special paths not crossing I mean something like this: