Hello, Codeforces!
A few days ago MohammadParsaElahimanesh posted a blog titled Can we find each Required node in segment tree in O(1)? Apparently what they meant was to find each node in $$$\mathcal{O}(ans)$$$, according to ecnerwala's explanation. But I was too dumb to realize that and accidentally invented a parallel node resolution method instead, which speeds up segment tree a lot.
A benchmark for you first, with 30 million RMQ on a 32-bit integer array of 17 million elements. It was run in custom test on Codeforces on Apr 6, 2021.
- Classic implementation from cp-algorithms: 7.765 seconds, or 260 ns per query
- Optimized classic implementation: (which I was taught) 4.452 seconds, or 150 ns per query (75% faster than classic)
- Bottom-up implementation: 1.914 seconds, or 64 ns per query (133% faster than optimized)
- Novel parallel implementation: 0.383 seconds, or 13 ns per query (400% faster than bottom-up, or 2000% faster than classic implementation)
FAQ
Q: Is it really that fast? I shamelessly stole someone's solution for 1355C - Count Triangles which uses prefix sums: 112167743. It runs in 46 ms. Then I replaced prefix sums with classic segment tree in 112168469 which runs in 155 ms. The bottom-up implementation runs in 93 ms: 112168530. Finally, my novel implementation runs in only 62 ms: 112168574. Compared to the original prefix sums solution, the bottom-up segment tree uses 47 ms in total, and the parallel implementation uses only 16 ms in total. Thus, even in such a simple problem with only prefix queries the novel implementation is 3x faster than the state of art even in practice!
Q: Why? Maybe you want your $$$\mathcal{O}(n \log^2 n)$$$ solution to pass in a problem with $$$\mathcal{O}(n \log n)$$$ model solution. Maybe you want to troll problemsetters. Maybe you want to obfuscate your code so that no one would understand you used a segment tree so that no one hacks you (just kidding, you'll get FST anyway). Choose an excuse for yourself. I want contribution too.
Q: License? Tough question because we're in CP. So you may use it under MIT license for competitive programming, e.g. on Codeforces, and under GPLv3 otherwise.
Q: Any pitfalls? Yes, sadly. It requires AVX2 instructions which are supported on Codeforces, but may not be supported on other judges.
How it works
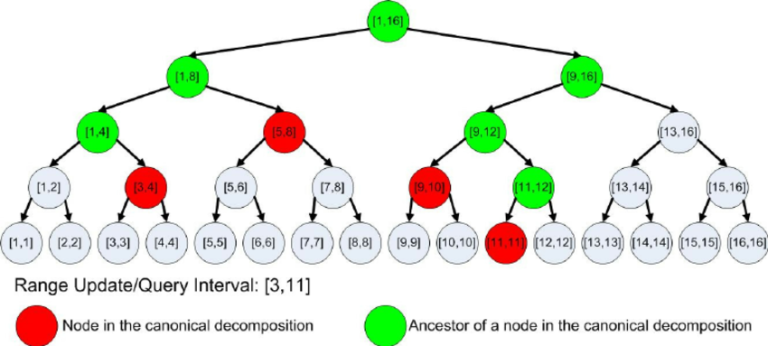
In a segment tree, a range query is decomposed into 'red' nodes. Classic segment tree implementations don't find these red nodes directly, but execute recursively on green nodes. Bottom-up segment tree implementation does enumerate red nodes directly, but it also enumerates a few other unused nodes.
The parallel implementation is an optimization of bottom-up tree. Probably you all know how bottom-up implementation looks like, but I'll cite the main idea nevertheless to show the difference between bottom-up and parallel implementations:
In bottom-up segment tree, we find the node corresponding to the leftmost element of the query, i.e. $$$x[l]$$$, and the node corresponding to the rightmost query element, i.e. $$$x[r]$$$. If we numerate nodes in a special way, the leftmost element will correspond to node $$$N+l$$$ and the rightmost will correspond to node $$$N+r$$$. After that, the answer is simply the sum of values of all nodes between $$$N+l$$$ and $$$N+r$$$. Sadly there are $$$\mathcal{O}(n)$$$ of those, but we can do the following optimization:
If $$$N+l$$$ is the left child of its parent and $$$N+r$$$ is the right child of its parent, then instead of summing up all nodes in range $$$[N+l, N+r]$$$, we can sum up all nodes in range $$$[\frac{N+l}{2}, \frac{N+r-1}{2}]$$$. That is, we replace the two nodes with their two parents. Otherwise, if $$$N+l$$$ is the right child of its parent, we do ans += a[N+l]; l++;, and if $$$N+r$$$ is the left child of its parent, we do ans += a[N+r]; r--; Then the condition holds and we can do the replacement.
In parallel segment tree, we jump to i-th parent of $$$N+l$$$ and $$$N+r$$$ for all $$$i$$$ simultaneously, and check the is-left/right-child conditions in parallel as well. The checks are rather simple, so a few bit operations do the trick. We can perform all bitwise operations using AVX2 on 8 integers at once, which means that the core of the query should run about 8 times faster.
Want code? We have some!
This is the benchmark, along with the four segment tree implementations I checked and a prefix sum for comparison.
The core is here:
The following line configures the count of elements in segment tree. It must be a power of two, so instead of using 1e6 use 1 << 20:
const int N = 1 << 24;
The following line sets the type of the elements. It must be a 32-bit integer, either signed or unsigned, at the moment.
using T = uint32_t;
The following line sets the identity element. It's 0 for sum, -inf for max, inf for min. If you use unsigned integers, I'd recommend you to use 0 for max and (uint32_t)-1 for min.
const T identity_element = 0;
The following function defines the operation itself: sum, min, max, etc.
T reduce(T a, T b) {
return a + b;
}
Then the following two functions are like reduce(T, T) but vectorized: for 128-bit registers and 256-bit registers. There are builtins for add: _mm[256]_add_epi32, min (signed): _mm[256]_min_epi32, max (signed): _mm[256]_max_epi32, min (unsigned): _mm[256]_min_epu32, max (unsigned): _mm[256]_max_epu32. You can check Intel Intrinsics Guide if you're not sure.
__attribute__((target("sse4.1"))) __m128i reduce(__m128i a, __m128i b) {
return _mm_add_epi32(a, b);
}
__attribute__((target("avx2"))) __m256i reduce(__m256i a, __m256i b) {
return _mm256_add_epi32(a, b);
}
Finally, these lines in main() are something you should not touch. They build the segment tree. Make sure to fill the array from a[N] to a[N*2-1] before building it.
for(int i = N - 1; i >= 1; i--) {
a[i] = reduce(a[i * 2], a[i * 2 + 1]);
}
a[0] = identity_element;
Further work
Implement point update queries in a similar way. This should be very fast for segment-tree-on-sum with point += queies, segment tree on minimum with point min= and alike.
Unfortunately BIT/fenwick tree cannot be optimized this way, it turns out 1.5x slower.
Contributions are welcome.











Auto comment: topic has been updated by purplesyringa (previous revision, new revision, compare).
Hey! If you don't mind, can you share your 'Optimized classic implementation' as well?
Sure! It's in the benchmark code. Copied here for you:
Classic:
Optimized:
The difference between the two is that the optimized implementation does not perform recursive calls if the node doesn't intersect with the query, while the classic implementation performs the recursive call but returns immediately.
While it's quite cool. I think it is way too limited to be useful :( Looks like it breaks if you have lazy or a harder operation. For example, $$$ \prod_{i=l}^{i=r} a_i \mod M$$$ (64 bit multiplications are pain in the ass, aren't they?). One thing I wanted to try but never actually did is trees with more than 2 children(base 4,8). Have you tried that, does it suck?
This implementation doesn't work with push operations, but something like range add can be implemented.
Add
modarray, and state that the value at indexxis equal toa[N+x] + mod[(N+x)/2] + mod[(N+x)/4] + ... + mod[1]. So ifmod[v] = c, it means to addcto all elements in the subtree ofv.Then the sum in $$$[l, r]$$$ is the sum of $$$a[v]$$$ of red nodes plus sum of $$$mod[v] \cdot X$$$ of green nodes, where X is the length of intersection of $$$[l; r]$$$ and $$$[vl; vr]$$$. All of that can be calculated in parallel.
As for multiplication modulo M, the problem is to provide a fast enough vectorized
reduce; there are some methods for that that I'm checking right now. I'm not sure if they'll be fast enough though.As for trees with more children, I think the classic argument applies here that the most efficient tree is a tree with exactly $$$e \approx 2.7$$$ children per node. So it only makes sense to consider trees with 2 or 3 children. The first case is segment trees, the second case is (somewhat) 2-3 trees.
I think the issue with range updates is that there are no scatter intrinsics until AVX512, so you'll just have to do slow scattering.
"I was too dumb to understand someone's question so I developed an algorithm that's 2000% faster than the cp-algos implementation. Oh yeah and also got 230 upvotes on CF"
Fenwick tree: 112298366 Can you add comparison with Fenwick tree too?
I have read and retested it. Code: https://www.ideone.com/GeqRbp (added comparison with Fenwick tree)
Note: author's code has poor random, because $$$l, r \in [0, \text{RAND_MAX}]$$$, where $$$\text{RAND_MAX} = 32767$$$ on Windows.
My conclusions: 1) If length of queries is small, e. g. $$$l, r \in [0, 32767]$$$ (as in author's code), query_parallel faster ~500% than query_bottom_up, and query_parallel faster ~170% than query_fenwick. 2) If length of queries is not small, e. g. $$$l, r \in [0, N]$$$, query_parallel faster ~170% than query_bottom_up, and query_parallel faster ~117% than query_fenwick.
So if queries' length is small avx segment tree works very well, but if length of queries is not small we have not appreciable win (on my laptop there is no win).