plz help me with this D-query problem .
→ Pay attention
Contest is running
2023 Post World Finals Online ICPC Challenge powered by Huawei
10 days
Register now »
2023 Post World Finals Online ICPC Challenge powered by Huawei
10 days
Register now »
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3690 |
| 2 | jiangly | 3647 |
| 3 | Benq | 3581 |
| 4 | orzdevinwang | 3570 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | Radewoosh | 3509 |
| 8 | ecnerwala | 3486 |
| 9 | jqdai0815 | 3474 |
| 10 | gyh20 | 3447 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 160 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | orz | 146 |
| 9 | pajenegod | 145 |
| 9 | SecondThread | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: May/11/2024 04:18:22 (j3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











there is simple NlogN offline solution:
are you sure this will work ? like for input- 1 2 3 4 1 2
after preprocessing cnt array will be like this cnt- 0 0 1 1 1 1
so for query [1,5] your answer will be sum=0+0+1+1+1=3 but actual anser will be 4
if indexes starts since 0, the sum will be 0+1+1+1+1==4. it seems it's right code.
What if the query was [1,1] — answer 0?!
just try it. implement & run code above, if you can't understand it. my version
wow,simple wow! such a beauty! :*
Thats a beautiful solution. Thanks
How can someone possibly think of such a solution unless he has solved a similar problem in past?
e-maxx.ru has it also
Wow..great idea brother.
wow
Since the problem's name contains the word "query" u had better use query-oriented language like SQL
Does anybody know how to solve this if you can change elements also?
Something similar to this.
It can be done in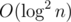 per query, for every two indices l, r such that l < r, al = ar and there is no such index x such that al = ax and l < x < r, store the 2D point (l, r) in some 2D data structure. The answer to a query is the length of the segment minus the number of points inside some rectangle. Which one, you may ask? This is left as an exercise for the reader!
per query, for every two indices l, r such that l < r, al = ar and there is no such index x such that al = ax and l < x < r, store the 2D point (l, r) in some 2D data structure. The answer to a query is the length of the segment minus the number of points inside some rectangle. Which one, you may ask? This is left as an exercise for the reader!
this is the same problem that u are asking https://www.hackerrank.com/contests/algoelite-v18/challenges/escaping-black-holes-v18
http://pastebin.com/j9g9CHAL
It can be solved online too with the same NLogn method using persistent segment tree
that's how i did it
Can you provide some links where I can learn Persistent Segment Trees ??
http://blog.anudeep2011.com/persistent-segment-trees-explained-with-spoj-problems/
Mo's Algorithm which runs in O(NsqrtN) works in time and is fairly easy to code. I used C++, so some slower languages may get TLE.
i am still getting tle
include<bits/stdc++.h>
using namespace std;
int main() { int n,p,count; scanf("%d",&n);
int a[n+1]; int pos[1000001]={0}; int cnt[n+1]={0}; for(int i=1;i<=n;i++) scanf("%d",&a[i]); scanf("%d",&p); pair<int,int> q[p+1]; int ans[p+1]; for(int i=1;i<=p;i++) { scanf("%d%d",&q[i].first,&q[i].second); } for(int i=1;i<=n;i++) { if(pos[a[i]]!=0) cnt[pos[a[i]]]--; pos[a[i]]=i; cnt[pos[a[i]]]++; for(int m=1;m<=p;m++) { count=0; if(q[m].second==i) { for(int k=q[m].first;k<=q[m].second;k++) count+=cnt[k]; ans[m]=count; } } } for(int m=1;m<=p;m++) { printf("%d\n",ans[m]); } }
you need to use a segment tree or a Fenwick tree to calculate sum from q[m].first to q[m].second in O(log n) time.
it still is giving tle.
include<bits/stdc++.h>
using namespace std; int tree[6000000]; void build(int node, int start, int end,int *cnt) { if(start == end) { // Leaf node will have a single element tree[node] = cnt[start]; } else { int mid = (start + end) / 2; // Recurse on the left child build(2*node, start, mid,cnt); // Recurse on the right child build(2*node+1, mid+1, end,cnt); // Internal node will have the sum of both of its children tree[node] = tree[2*node] + tree[2*node+1]; } } int query(int node, int start, int end, int l, int r) { if(r < start or end < l) { // range represented by a node is completely outside the given range return 0; } if(l <= start and end <= r) { // range represented by a node is completely inside the given range return tree[node]; } // range represented by a node is partially inside and partially outside the given range int mid = (start + end) / 2; int p1 = query(2*node, start, mid, l, r); int p2 = query(2*node+1, mid+1, end, l, r); return (p1 + p2); } int main() { int n,p,count; scanf("%d",&n);
int a[n+1]; int pos[1000001]={0}; int cnt[n+1]={0}; for(int i=1;i<=n;i++) scanf("%d",&a[i]); scanf("%d",&p); pair<int,int> q[p+1]; int ans[p+1]; for(int i=1;i<=p;i++) { scanf("%d%d",&q[i].first,&q[i].second); } for(int i=1;i<=n;i++) { if(pos[a[i]]!=0) cnt[pos[a[i]]]--; pos[a[i]]=i; cnt[pos[a[i]]]++; build(1,1,i,cnt); for(int m=1;m<=p;m++) { if(q[m].second==i) { ans[m]=query(1,1,i,q[m].first,q[m].second); } } } for(int m=1;m<=p;m++) { printf("%d\n",ans[m]); } }
MO's algorithm + printf/scanf gives AC. Here is my code
I referred this article to make an editorial on the problem. It uses Mo's algorithm, which is offline query processing, to solve the problem in N*sqrt(N). Here is the video link.
I'm getting WA on my code. I used MO's algorithm. Can anybody tell me why ? Link to my code
I wrote an answer about it on Quora.