349A - Cinema Line
In the problem you need to decide whether cashier can give a change to all customers if the price of the ticket is 25 rubles and there's 3 kinds of bills: 25, 50 and 100 rubles. There's no money in the ticket office in the beginning.
Let's consider 3 cases.
- Customer has 25 rubles hence he doesn't need a change.
- Customer has 50 rubles hence we have to give him 25 rubles back.
- Customer has 100 rubles hence we need to give him 75 rubles back. It can be done in 2 ways. 75=25+50 и 75=25+25+25. Notice that it's always worth to try 25+50 first and then 25+25+25. It's true because bills of 25 rubles can be used both to give change for 50 and 100 rubles and bills of 50 rubles can be used only to give change for 100 rubles so we need to save as much 25 ruble bills as possible.
The solution is to keep track of the number of 25 and 50 ruble bills and act greedily when giving change to 100 rubles — try 25+50 first and then 25+25+25.
349B - Color the Fence
In the problem you're asked to write the largest possible number given number of paint that you have and number of paint that you need to write each digit.
Longer number means larger number so it's worth to write the longest possible number. Because of that we choose the largest digit among those that require the least number of paint. Let the number of paint for that digit d be equal to x, and we have v liters of paint total. Then we can write number of the length 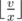 .
.
Now we know the length of the number, let it be len. Write down temporary result – string of length len, consisting of digits d. We have supply of v–len·x liters of paint. In order to enhance the answer, we can try to update the number from the beginning and swap each digit with the maximal possible. It's true because numbers of the equal length are compared in the highest digits first. Among digits that are greater than current we choose one that we have enough paint for and then update answer and current number of paint.
If the length of the answer is 0 then you need to output -1.
348A - Mafia
In the problem you need to find out how many games you need to play in order to make all people happy. It means that each of them played as many games as he wanted.
Let the answer be x games. Notice that max(a1, a2, …, an) ≤ x. Then i-th player can be game supervisor in x–ai games. If we sum up we get 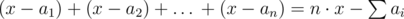 — it's the number of games in which players are ready to be supervisor. This number must be greater or equal to x — our answer.
— it's the number of games in which players are ready to be supervisor. This number must be greater or equal to x — our answer.
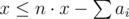
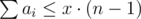
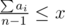
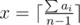
Don't forget about that condition: max(a1, a2, …, an) ≤ x.
348B - Apple Tree
In the problem you need to find out minimal number of apples that you need to remove in order to make tree balanced.
Notice, that if we know the value in the root then we know values in all other vertices. The value in the leaf is equal to the value in the root divided to the product of the powers of all vertices on the path between root and leaf.
For every vertex let's calculate di — minimal number in that vertex (not zero) in order to make tree balanced. For leaves di = 1, for all other vertices di is equal to k·lcm(dj1, dj2, ..., djk), where j1, j2, ..., jk — sons of the vertex i. Let's calculate si — sum in the subtree of the vertex i. All that can be done using one depth first search from the root of the tree.
Using second depth first search one can calculate for every vertex maximal number that we can write in it and satisfty all conditions. More precisely, given vertex i and k of its sons j1, j2, ..., jk. Then if m = min(sj1, sj2, ..., sjk) and 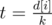 — minimal number, that we can write to the sons of vertex i, then it's worth to write numbers
— minimal number, that we can write to the sons of vertex i, then it's worth to write numbers 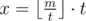 to the sons of vertex i. Remains
to the sons of vertex i. Remains  we add to the answer.
we add to the answer.
348C - Subset Sums
This problem is about data structures.
First step of the solution is to divide sets to heavy and light. Light ones are those that contains less than  elements. All other sets are heavy.
elements. All other sets are heavy.
Key observation is that every light set contains less than  elements and number of heavy sets doesn't exceed
elements and number of heavy sets doesn't exceed  because we have upper bound for sum of the sizes of all sets.
because we have upper bound for sum of the sizes of all sets.
In order to effectively answer queries, for every set (both light and heavy) we calculate size of the intersection of this set and each heavy set. It can be done with time and memory 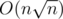 . For every heavy set we create boolean array of size O(n). In i-th cell of this array we store how many elements i in given set. Then for each element and each heavy set we can check for O(1) time whether element is in the set.
. For every heavy set we create boolean array of size O(n). In i-th cell of this array we store how many elements i in given set. Then for each element and each heavy set we can check for O(1) time whether element is in the set.
Now let's consider 4 possible cases:
Add to the light set. Traverse all numbers in the set and add the value from the query to each of them. Then traverse all heavy sets and add (size of intersection * the value from the query). Time is
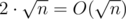 .
.Add to the heavy set. Just update the counter for the heavy set. Time is O(1).
Answer to the query for the light set. Traverse all numbers in the set and add values to the answer. Then traverse all heavy sets and add to the answer (answer for this heavy set * size of intersection with the set in the query). Time is
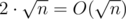 .
.Answer to the query for the heavy set. Take already calculated answer, then traverse all heavy sets and add (answer for this heavy set * size of intersection with the set in the query). Time is
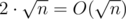 .
.
We have O(n) queries so total time is 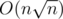 .
.
348D - Turtles
In the problem you're asked to find the number of pairs of non-intersecting paths between left upper and right lower corners of the grid. You can use following lemma for that. Thanks to rng_58 for the link. More precisely, considering our problem, this lemma states that given sets of initial A = {a1, a2} and final B = {b1, b2} points, the answer is equal to the following determinant:
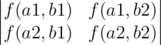
Finally we need to decide what sets of initial and final points we choose. You can take A = {(0, 1), (1, 0)} and B = {(n - 2, m - 1), (n - 1, m - 2)} in order to make paths non-intersecting even in 2 points.
348E - Pilgrims
Let’s build a simple solution at first and then we will try to improve it to solve problem more effectively given the constraints.
For every vertex let’s find the list of the farthest vertices. Let’s find vertices on the intersection of the paths between current vertex and each vertex from the list that don’t contain monasteries. If we remove any of these vertices then every vertex from the list is unreachable from the current monastery. For every vertex from the intersection increment the counter. Then the answer for the problem is the maximum among all counters and the number of such maxima.
Let’s solve the problem more effectively using the same idea. Let’s make the tree with root. For every vertex we will find the list of the farthest vertices only in the subtree. While traversing the tree using depth first search we return the largest depth in the subtree and the number of the vertex where it was reached. Among all of the sons of the current vertex we choose the maximum of depths. If maximum is reached one time then we return the same answer that was returned from the son. If the answer was reached more than one time then we return the number of the current vertex. Essentially, we find LCA of the farthest vertices according to the current vertex. Before quitting the vertex we increment the values on the segment between current vertex and found LCA. One can use Eulerian tour and segment tree for adding on the segment.
Finally, the last stage of solving the problem – to solve it for the case when the farthest vertex is not in the subtree of the current vertex. For solving of that subproblem we use the same idea that was used in the problem of the finding the maximal path in the tree. For every vertex we keep 3 maximums – 3 farthest vertices in the subtree. When we go down to the subtree, we pass 2 remaining maximums too. In that way, when we’re in any vertex, we can decide whether there’s a path not in the subtree (it means, going up) of the same or larger length. If there’re 2 paths of the same length in the subtree and not in the subtree, it means that for the pilgrim from the current monastery there’s always a path no matter what town was destroyed. If one of the quantities is larger then we choose the segment in Eulerian tour and increment the value on the segment. The case where there’s several paths (at least 2) out of the subtree of the same maximal length, is the same with the case in the subtree.
LCA and segment tree can be solved effectively in O(logN) time per query so the total memory and time is O(NlogN).











Very nice idea for problem D. :) It's actually possible to solve problem E in O(n) time. LCA is not necessary, the "counting" process can be done by two dfs, first count the occurences of nodes in the "going up" part of paths, then count the occurences of nodes in the "going down" parts. You may see my solution for detail..
There's actually no need to use binary search in problem C, when finding intersections of sets. A brute-force implementation consumes only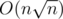 time.
time.
I still don't get how it's done. There are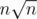 intersections to calculate, and each one takes n time..
intersections to calculate, and each one takes n time..
For each element of each set see if it's contained in each big set (storing big sets in boolean arrays). There are N elements in total and big sets, so it's
big sets, so it's 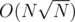 time and space.
time and space.
Ah, that's a nice way to analyze it. And if we use binary search instead of boolean array, it'll be n*sqrtn*logn. But then I don't get the n*sqrtn "brute force" approach.
I guess huzecong meant boolean arrays for big sets.
Sorry for not being clear, but a boolean array was what I meant... I thought that compared to the binary search approach this one seems pretty "brute-force"...
In the editorial we defined heavy sets to be those which contained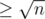 elements. Denoting
elements. Denoting 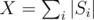 , we have atmost
, we have atmost 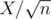 heavy sets. If we go through each element of each set (X of those) and check if its contained in every heavy set (
heavy sets. If we go through each element of each set (X of those) and check if its contained in every heavy set (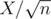 of those), we have a complexity of
of those), we have a complexity of 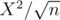 which is out of limits. Am I missing anything?
which is out of limits. Am I missing anything?
According to problem statement, It is guaranteed that the sum of sizes of all sets Sk doesn't exceed 10^5. Naive solution works in (10^5)*(10^5)/sqrt(10^5), it is just few hundred millions of operations.
X ≤ 105, but with small n (like 4),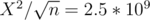 which is TLE? In the editorial is X = n ?
which is TLE? In the editorial is X = n ?
If you'll take heavy_size>=sqrt(X) — it will be ok, right? :)
I am not sure, but it looks like you are right, taking heavy_size>=sqrt(n) is bad idea.
But it will pass system tests) It do not proves that this solution is OK, it just shows us that tests are very weak. Take a look at 7288633, TsunamiNoLetGo has array for heavy sets of size 320 only, and heavy_size>=sqrt(n). It is easy to constuct testcase with 100000 heavy sets — just take n=1, m=100000, and all sets of size 1. But this solution passed, therefore i guess that such cases are missed in testdata.
Yes thats exactly what I meant. Setting heavy_size >= sqrt(X) is okay with me. SealView also told me that in the messages. He advises to set it to a constant (like 300). Thanks for looking into my problem. :D
in problem Apple trees can somebody explain the idea of finding intersections of sets using binary search
I think, you're talking about "Subset sums" problem.
Sort all lists. Iterate over one set and check whether element from this set is in another set. You can do it using binary_search() function from STL.
no apple trees 348B
There is no binary search and no sets in 348B.
I get a memory limit on problem Apple Tree. here is my submission : http://codeforces.com/contest/348/submission/4630566 Anybody knows why ?
The leaf of the Apple Tree can be 0. So lcm can be zero.
Can someone explain 348A — Mafia with more details, please? :|
Let's say you're going to play x games. If someone wanted to play more than x games, he wouldn't be able to do so, so he would be unhappy. Therefore, if everyone is happy, x ≥ ai must hold for each i, so
Let $b_i$ be number of games, where i-th player is supervisor and let ci be number of games, where he plays. In each game i-th player is playing, XOR supervising, so ci + bi = x. Also, he wants to play at least ai games, so ai ≤ ci, thus bi ≤ ci + bi - ai, so bi ≤ x - ai.
Each game is supervised by one player, so x = b1 + b2 + ... + bn. Giving it all together:
Now we have two lower bounds for $x$ . Smallest x satisfying both of them is
This number of games is enough, because if first $x - a_1$ games are supervised by first player, next x - a2 games are supervised by second player etc., until the x-th game, then everyone plays enough games and each game is supervised by someone.
In 348A-Mafia, How does this condition ensures that the value of 'x' found is minimum?
We simple do the binary search. Because of the principle of the binary search. We wouldn't be able to decrease x lower that lower bound in binary search(we checked the lower bound and found it impossible to fulfill the conditions by making only "lower bound" number games), similar for upper bound.
read discrete binary search from topcoder...you will understand
can some one explain following line from apple tree editorial. Line : The value in the leaf is equal to the value in the root divided to the product of the powers of all vertices on the path between root and leaf. how this come ?
value in a node = weight of a node.
power of a node = number of children of a node.
Let the value in the parent be X and power of it be K. Then value in each of its children will be X/K, as values of each children needs to be equal. Example:
A is the root and D is a leaf.
A (weight:X, power:3) --> B (weight:X/3, power:2) --> C (weight:X/(3*2), power:3) --> D (weight:X/(3*2*3)).
In Div. 1 Problem B, I didn't understand the idea behind d[i]. Why are we taking the lcm of all the children of the i'th vertex? What is the logic behind the solution. Could someone please help me out and elaborate?
Can someone provide a more detailed explanation for Div1 B ??
I don't know why does my solution for Div1B gets TLE... Can somebody help and take a look at it? Thanks in advance.
http://codeforces.com/contest/348/submission/19399532
Actually , We can solve Problem 348A-Mafia in a simpler way. let S = Σ a(i) for all i , c(i) = number of rounds played by the ith person so far , S2 = Σ c(i) for all i.
Then S2 is the Summation of the number of rounds played by each person so far. Actually , we need the number of Rounds X Which will make S2 >= S holds.
You Can Notice that after X Rounds , S2 Will be Equal to X*N — X , Were N is the number of People. Because simply , After each Round S2 will be incremented by the number of People -1 because all of them will play except one will be the supervisor.
So we just need to Search using Binary Search on the value X which will make X*N — X >= S holds .
NOTE : X should be >= max (a(i)).
Here is the link for my code.
20368610
Shouldn't we also need for all i (c[i]>=a[i]) after playing X rounds, & how does the condition S2>=S guarantees that
Problem B (div 2) has a tag of DP. how we can implement dp on this problem?
This may help.
thankyou hmrockstar your solution was great!!
DIV 2 B has dp tag, but it's a greedy problem :/
Div1 B, when we are calculating d[i] we are not considering the children of other nodes of the same level ?? for example, if root has 2 children and one of them has 3 children and another one has 2 children then we need to have the lcm of both 3 and 2 which is 6. please help !!
Anudeep's Submission of Problem Div1 C https://codeforces.com/contest/348/submission/4596270
Close to editorial!!!
DP approach for Div2 problem B
We can use the DP solution below. The approach is simple known as reconstructing the solution where we keep storing the optimal path in terms of parent of the state and then when we want to print we backtrack on the parent array. https://codeforces.com/contest/349/submission/107398509
Great code man. Really loved the code and idea behind it. Have you done similar problems before or is this the only problem you have ever encountered with this type of logic?