Editorial for Codeforces Round #204
352A - Jeff and Digits
Solution is looking for few cases:
1. If we do not have zeros, then the answer is -1.
2. If we have less than 9 fives, then the answer is 0.
3. Otherwise, the answer is:
4. 1. The maximum number of fives divisible by 9
4. 2. All zeros, we have
352B - Jeff and Periods
We will go through the array from left to right. At each step, we will store the arrays:
1. nextx — the last occurrence of the number x
2. periodx — period, which occurs x
3. failx — whether a time when the number of x no longer fit
Now, when we get a new number we considering the case when it is the first, second or occurred more than twice.
All the cases described in any past system testing solution.
351A - Jeff and Rounding
Initially, we should remember the number of integers — C. On next step we will round down all numbers and count the sum. Now we can change the sum, rounding up some numbers, with those not matter what kind of, the main thing — how many. Consider a couple what we could get:
1. (int, int) (c1)
2. (int, double) (c2)
3. (double, int) (c3)
4. (double, double) (c4)
Iterate over the number of pairs of the first type. Then we know the total number of second and third type and number of the fourth type:
1. c2 + c3 = C - 2c1
2. c4 = N - (c1 + c2 + c3)
Check to see if you can get such numbers (enough for us count of integers and real numbers, respectively). We find that we can round up from c4 to c4 + c2 + c3 numbers. We will find the best choise.
351B - Jeff and Furik
ote that after each step, the number of inversions in the permutation is changed by 1. Let us turn to the inversions of the permutation — let them be I pcs. It is clear that when we have one inversion, then the answer — 1. Now we will see how to use it further:
1. it is clear that after a Jeff's step inversions will become lower by 1
2. it is clear that after a Furik's step inversions will be on 1 lowerwith porbability of 0, 5, and on 1 greater with probability of 0, 5.
3. we have the formula for an answer ansI = 1 + 1 + ansI - 1 - 1 × 0.5 + ansI - 1 + 1 × 0.5
4. after transformation we have ansI = 4 + ansI - 2.
351C - Jeff and Brackets
How to solve the problem for small NM? Just use the dynamic programming dpi, j — minimum cost to build i first brackets with the balance j. Transfers are simple:
1. dpi, j + ai + 1 -> dpi + 1, j + 1
2. dpi, j + bi + 1 -> dpi + 1, j - 1
3. we make transfers only when balance will be non-negative
4. starting state dp0, 0 = 0
In this problem, we can assume that the balance will never exceed 2N. The proof is left as homework.
And by using this fact problem can be done by erecting a matrix to the power:
1. lets Ti, j — cost of transfer from balance i to balance j, using N brackets
2. (TM)0, 0 — answer to the problem
351D - Jeff and Removing Periods
After the first request we can sort the numbers and for further moves will be able to remove all occurrences of a certain number. So the answer is the number of different numbers + 1 if there is no number, occurrence of which form an arithmetic progression.
Number of different numbers on a segment — standart problem, can be done O(N1.5) with offline algorithm.
The problem about finding the right number will be solved in a similar algorithm:
1. lets sort queries like pairs (li / 300, ri), we use integer dividing
2. learn how to move from the interval (l, r) to intervals (l - 1, r), (l + 1, r), (l, r - 1), (l, r + 1) with complexcity O(1)
3. by means of such an operation will move from one segment to the next, in the amount of the operation algorithm will works O(N1.5)
It remains to learn how to make the change on the interval by 1 element. Such a problem can be solved quite simply:
1. we craete deque for all value of numbers in array
2. depending on changes in the segment will add / remove items to the start / end of the respective deque
3. check whether the resulting deque is arithmetic progression. it will be homework.
351E - Jeff and Permutation
We make the zero step, replace the elements on their modules.
The first thing you need to understand the way in which we will build our response. After selecting a few ways to understand the fact that initially you need to determine the sign of the largest numbers.
Consider the case where the current step we have only one maximal element. It is clear that if you put a sign - all the elements on the left of this will form an inversion, while on the right there will be no inversions. If we do not put a sign - it will all be the opposite. We select the best one and cross out the number of the array, it will not affect to some inversion.
Now we should understand how to read the response when the highs more than one. We write the dynamics dp[i][j] — how much inversions can you get, when we looked at the first i higest values and j from them lefted as possitive. Of these dynamics is not difficult to make the transition and get the answer.
And so we have a simple and short algorithm:
1. Iterates until the array is not empty
2. Find all the maximal elements
3. Calculate dynamics and find right signs
4. Remove elements from an array











Please explain "351C — Jeff and Brackets" in more detail. Thanks!
First note that there is always an optimal bracket sequence such that none of its prefixes has a balance larger than 2N (there's a proof sketch somewhere below).
Now make a (2N+1)*(2N+1) matrix. In cell (i, j) write the cost of the optimal n-block that changes the total balance from i to j, such that at no point it goes below 0 or above 2N (this second thing is not necessary actually).
Now we raise this matrix to the m-th power in Max-Plus algebra. This is basically an algebra where you replace addition with max and multiplication with addition. So when you do matrix "multiplication", the inner assignment is C[i][j] = max(C[i][j], A[i][k] + B[k][j]), and you initialize C[i][j] to some large number ("infinity") beforehand. The interpretation of this is pretty straightforward. Let A and B represent the optimal costs of moving from some i to some j total balance using a and b n-blocks, respectively. Then C will represent the same thing using (a+b) n-blocks.
See my code in the practice room for details, or ask for clarifications if I messed something up in my explanation :)
Hi,
Thanks for the reply :)
It took me a while to understand the matrix exponentiation part. It is a very neat method. Can you provide some literature for this? Theory or other problems?
Thanks. PS: You meant min() in the expression for C[i][j].
[removed]
Can anyone share idea how to solve C(div. 1) without matrix multiplication?
I used doubling algorithm to do this problem.
A bracket sequence can be simplify to the form like
)))(((( = [')' * x + '(' * y]
So we can let f[k][i][j] denote, when we build (2^k * n) brackets, and they will simplify to [')' * i + '(' * j], we can assume that the balance will never exceed N(like sereja's solution).
We can get f[0] by iterator all possible bracket sequencen, and f[k] by merge two f[k — 1] when k > 0.Assume m = 2 ^ k1 + 2 ^ k2 + .. + 2 ^ kx, we just need to merge f[k1]~f[kx] to get the answer f[...][0][0].
I've got it. Thanks)
Can someone explain Jeff and rounding in more details ??
i see there are greedy solutions solving the problem, and also appreciated based on time complexity, but this is a straightforward dp solution which fits in the given constraints pretty well.
considering dp[n][f], where array[n] : n'th element of given array[], f : number of elements rounded down so far. integer portions of the input array elements are unnecessary, as they remain same in output sequence of rounded numbers. recursion is halted when n>2N [end of array] or f>N [more than N numbers are rounded down already]. notice that, we need N numbers to round down and the rest N to round up, so f needs to be N exactly.
then while processing dp(n,f), we can either round down the n'th number or otherwise. we attempt both of them and take the minimum based on their absolute difference of course.
My code goes here, http://codeforces.com/contest/351/submission/4674608
Any proof/explanation why absolute difference value can be found by this kind of recursion? I thought the recursion is only applied on searching max/min value. That's why I got stuck on this problem, I thought I needed another state (dp[index][rounded down value][the difference target]).
let's assume, input array is A, array to be made after rounding is B.
in this problem i have considered that the summation of the A array elements is always greater than the summation of the B array elements. so rounding-UP can only decrease the difference, hence deducted.
now from any state you need to calculate the minimum absolute difference to finish the job. recursion returns signed values, positive means input array has greater sum, and negative means otherwise.
notice, the ultimate difference is the summation of all the little differences we made on the way, i.e, increasing sum if a number is rounded down, and decreasing sum if a number is rounded up
now we need to minimize the "absolute" difference, not the signed differences, so we compare by the absolute value, and return the signed value, as we need to make a simple summation of the little differences for each array entry to find the output.
i tried to explain as simply as possible, apologies if it still seems confusing.
I am still confusing about the DP mythod. For example, the input data is as follows 3 0.000 0.200 0.600 0.600 0.200 0.000
Then when considering about dp[5][3], if the 5'th number rounding down, then the minimum abosolute value can get from dp[4][2]+(0.2). Right?
But dp[4][2] should be 0.4, but actually we can also rounding down 1'th and 2'th number to get -0.6, and |-0.6+(0.2)| < |0.4+(0.2)| . So we cannot get the right answer from the optimal subproblem, which is not like DP... we get the right answer for dp[5][3] is from the condition when the 5'th number is rounding up.
if you start recursion at (1,0) and head towards (2N,N), dp(n,f) means, you're processing the n'th element while f of the previous (n-1) elements are already rounded down. if dp(5,3) is called from dp(4,2), then it means 4th element was the 3rd number from the beginning which was rounded down, 5th element is yet to be processed . likewise, recursion is halted when n>2N, which is after processing of the 2N'th element in rec(2N,something).
very nice explanation, thank you :)
+1 for Rev.1! :) Very nice explanation indeed..;) Monmoy
thanks, i like the top-down aproach, is more easy to understand dp states and transitions
You can try some simple inputs and use different ways to choose which numbers are rounded up and which are rounded down. You will find that if the options we take on integers don't change, the result will be the same. Assume that we round down as many integers as possible, then simply calculate the result. Then if we reduce the number of integers rounded up by 1, the result will incrrease by 1. (Note:Here the result is signed, that means if the sum of new numbers is less than the original sum, the result is negative). If you notice these two points, finding the best answer will be very easy. Also the proof is simple too. So we just iterate on the number of integers we take rounded down, and in each step increase the result by 1, and update the best answer, until there aren't any integers are rounded down, or all round up numbers are integers. So in the program we just need to count the number of integers and calculate the initial answer(that can be done by sorting the numbers with the fractional parts), then the following work is easy. You can check my solution 4664512 for details.
Yours is the only method amongst others that I can understand and prove.
http://codeforces.com/blog/entry/9070?locale=en#comment-147569
i think this is a easy one for me to understand http://codeforces.com/contest/351/submission/4677352
Took me a while to understand the Greedy Approach. Lets say the input array is A[2n]. In this array, we have to ceil n numbers and floor n numbers. We modify the input array to store only the decimal portion of the numbers. The decimal portion of the numbers also represents the amount needed to Floor the Number. We take the sum of all numbers in A as S.
If the amount to floor a number is x, then the amount to ceil the same number is (1-x).
From the given array, if we choose two indexes i & j, where we choose to floor index i and ceil index j, then the total deviation from the S due to the rounding off of the given pair would be :
Amount required to Ceil index j - Amount required to floor index i= (1-A[j]) - A[i], where A[i] and A[j] is the amount required to floor the number at index i & j respectively.Now
(1-A[j]) - A[i] = 1 - A[j] - A[i] = (1-A[i]) - A[j]Which implies that it doesnt matter which number you choose to ceil or floor in the given pair.Now the TOTAL deviation from S due to all such pairs would be given by :
where (j_1, i_1), (j_2, i_2), ....., (j_n, i_n) are the indexes that form a pair.
The answer would have been this, but since some numbers in the array can be integers to begin with, the amount required to round them off (whether ceil or floor) is equal to 0. But in the above equation we have ceiled some of these numbers and added '1' to the total. Hence run a loop :
We are running the loop till Min( Count(Integers in A),n ) , since we can ceil at max n numbers.
4679640
A more simpler approach (for me) but O(N*2001) was to use DP. DP(i,j) = the minimum deviation from S by using the first i numbers in A and ceiling exactly j of those numbers.
The recurrence relation would be :
The final answer would be in DP(2n,n) since we need the minimum deviation by using the entire array of size 2n and ceiling exactly n numbers.
4675561
Thank you, this was a fantastic explanation.
For 351A — Jeff and Rounding, my solution is: First, we count the integer numbers, and suppose all the real numbers round up. Then, we count the total difference. For not integer numbers, we change it to round down, the total difference will down by 1. So, we just need to enumerate the number of real numbers which should round down, and find the best solution.
I think your "352A" are wrong. Eighteen fives are not divisible by 9.https://www.google.co.th/search?q=555555555555555555%2F9&oq=555555555555555555%2F9&aqs=chrome.0.69i59l2j0.7908j0&sourceid=chrome&ie=UTF-8
Next time use a better tool before making such a claim: https://www.wolframalpha.com/input/?i=555555555555555555%2F9
A number is divisible by 9 iff the sum of its digits is divisible by 9, and 18·5 is divisible by 9.
Could you please explain me why all 0 are placed after digit 5?
Because we have to choose the largest such number. For a number to divisible by 9, its sum has to be divisible by 9. Thus, the largest such number divisible by 90 would be having all 5s in the higher ordered digits. Eg 505 is smaller than 550 while both have same sum of digits.
Can someone please explain the correlation between problem Jeff And Rounding with 2SAT and flows. I found the problem tagged with these.
Okay the tags have now been updated and I look like a fool. :P
Sorry, but can someone tell me, what's wrong with my code for Div.2 C? I read a lot of different submission and solutions and found out thet my idea was true! But i can't find my mistake:( Thank you! My code here:4670052 Maybe something is wrong with K or with double numbers, but i don't think so... Please, help me!
Please explain why balance never exceed N — div1 C. I tried to understand that with Pigeon hole principle but failed..
I'll prove that there is always an optimal (i.e. cheapest) bracket sequence where the prefix balance never exceeds 2N. This differs from what you said only slightly in that it is possible that a prefix balance exceeds 2N in many optimal solutions (I know you're probably aware of this, just trying to be precise), and also that I'm using 2N instead of N (2N is what is suggested by the editorial).
Anyway, this is the proof. Take any optimal bracket sequence. If no prefix balance is above 2N, then we are done. Otherwise, find the leftmost n-block inside which the prefix balance exceeds 2N (let's call this n-block block X). At the end of this block, the current balance is surely larger than N, so that must mean that there are some n-blocks to the right that have a negative total balance (because we must end on balance 0).
On the other hand, just before block X the prefix balance is strictly larger than N (block X could only have added N). That means that we can safely add any n-block from the right with a negative balance (because even if its balance is -N, the prefix balance will still not go negative). Now, the prefix balance inside X decreases, but it still might be larger than 2N (also note that it is surely >0 because it was >N before the move). If it is, you repeat the procedure (all the preconditions are the same as just before we made this one move).
You can repeat this until the claim is met.
Now, it might be possible to adjust this to just N, but proving that doesn't seem as easy if it is even true to begin with.
Edit: I forgot to address the issue that when you decrease this prefix balance, somewhere in the optimal solution you might get a negative prefix balance (i.e. an invalid sequence). You can fix this in a very similar manner.
maybe I don't understand the problem statement... could someone tell me what's wrong with this:
N=1, M=6 and consider the sequence "((()))"
so at the third position, i.e. "(((", the balance is 3 > 2*1 = 2*N
The point is that your example is allowed, but it is never necessary to go above 2N. For example if N=1 then "()()()" is identical to "((()))".
Basically the imbalance of a string of length N is at maximum N. If you have one of the substrings of length N taking the imbalance above 2N, you could equally put that after a later substring that decreases the imbalance, and the result would be the same.
Key point of your proof is, when 2n exceed-balance occurs, get the right position of n-unit blocks then add some n-unit blocks to decrease balance. I hope I got your idea correctly. But it is difficult to me to understand some detail parts.
In paragraph 2, I cannot get the exact position of block X. Would you mind if you explain it with a simple example?
In your idea, to decrease the exceeded balance, we have to add some n-unit blocks. I think in that way, the length of optimal solution becomes longer and longer. Does that point have any problems at all?
Say N=3 and M=6 and this is one optimal solution (I will use + to denote the left brace, and — to denote the right brace)
+++ +++ ++- --+ — --- 1 2 3 4 5 6
Under the n-blocks I wrote their number. So, block X is the leftmost n-block where the prefix balance exceeds 2N=6. In this case, that will be block 3.
Now, for your question 2, perhaps I didn't write that as clearly, but you never add any new n-blocks or change them. You just reorder them.
So here, you would take block 4 and put it before block X
+++ +++ --+ ++- — --- 1 2 4 3 5 6
Now that we've done that, we can see that the highest prefix balance inside block X decreased (it was 8 before, now it is 7) but it is still higher than 2N, so we repeat the procedure.
+++ +++ --+ — ++- --- 1 2 4 5 3 6
And now we're done.
Btw, I'm not entirely sure how to fix the problem that somewhere on the right your prefix balance might become negative (what I wrote in the edit). I think you should always pick the leftmost negative n-block to the right of block X when fixing block X, and that ensures that any remaining negative n-blocks to the right will be correct (because their whole prefix is the same, just reshuffled). However, there is a sequence of non-negative n-blocks between block X (after it has been fixed) and that first negative n-block (if any), and some of these non-negative n-blocks could contain negative prefixes which might get the whole prefix balance negative which is a problem. In the few minute I've been now thinking about this problem, I haven't been able to figure it out so hopefully someone else can or can show that this "proof" is in fact invalid and provide a correct one :)
Meh, I'm sorry, I just can't format this, the editor is pretty bad :(
Oh, you mean "reordering", not "add". I understood wrong about that. So much thanks for the example that I can get your idea clearly. Of course either I cannot sure about negative balance problem what you worry about, but it is hard to come up with counter-example of your proof for me.. It seems that it is always possible to reorder the n-unit sequence without occurring negative balance.. Anyway so much thanks for your help. Thanks very much.
Actually, I think I've found a proof (sketch) for N that is fairly simple, except some hairiness at the end. Here it is, please let me know if it's wrong :) (my code that uses it is here 4708757, it passes systests but that obviously doesn't mean it's right :)
Theorem: There is always an optimal sequence such that no prefix balance exceeds N.
Definition: We call an N-block positive if it has strictly more than N div 2 opening braces. We call an N-block negative if it has strictly more than N div 2 closing braces.
Now, let's take any optimal sequence. Let's call the first N-block in which the prefix balance exceeds N block X (as before).
Lemma 1: There must be at least one positive N-block to the left of block X. Proof of Lemma 1: Block X can't be the first block in the sequence because then the largest prefix balance could only be N. Furthermore, before block X, the prefix balance must be at least 1. Therefore, we must have had at least one positive N-block.
Lemma 2: There must be at least one negative N-block to the right of block X. Proof of Lemma 2: Block X can't be the last block because at its end, the balance will be at least 2 [the case where N is the balance at the start of block X, then X is ())))...))]. Furthermore, the balance after block X must be strictly positive so we must have at least one negative N-block to get to balance 0 at the end.
Proof of Theorem: Due to Lemmas 1 and 2, we can find at least one positive N-block to the left of block X and at least one negative N-block to the right of block X. Let's call them A (positive) and B (negative). Now, by the definitions of positive and negative N-blocks, in at least one of the N positions, A has an opening brace and B has a closing brace. Therefore, we can reduce the prefix balance inside block X by one by swapping these two braces in blocks A and B.
Now, there's again the problem that bothered me in the other "proof", i.e. when we do that, some prefix that had balance 0 before we made this change now might have balance -1. I have an idea how to fix that that I think will work but it's pretty complicated and I can't really write it all down. The rough idea is to pick A and B as close as possible to block X. Furthermore, you can do some swaps very similar to what I described so that all the blocks between A and X and between X and B are balance neutral (i.e. their total balance is 0). Then you pick the leftmost of these balance neutral blocks (i.e. that one closest to A) instead of B and make the swap between it and A (you can still do it because A has strictly more than (N div 2) opening braces and the balance neutral block has exactly (N div 2) closing braces so they must overlap in at least one position).
Btw, I think the other proof can easily be made to work for 3N (which is plenty sufficient for this problem). When you fix block X, the balance after X will still be larger than N. Therefore, the 0-balance N-blocks that remain after X will not be able to make the prefix balance negative because their "negative peaks" can only be -(N div 2) "high".
When you swap an opening brace with a closing brace,the answer of the sequence will change(that is to say,the new sequence is not optimal).Unless the index of the opening brace has the same remainder with the closing one`s.
But when you exchange two blocks, the answer will not change.
I have studied your proof for hours.But I think both of them are not completely right,as you said above.And this problem confuses me.
If you have any idea,please share with me,thank you :)
ps:forgive my poor english
In this "second proof", you always swap an opening and a closing brace that are at the same position within an N-block (i.e. their positions in the sequence are the same modulo N), so the cost of the sequence never changes.
I'm pretty sure the "first proof" is correct for a bound of 3N, and the "second proof" can be made to work for a bound of 2N.
In "second proof", how can you prove that we can find two braces with their index have same modulo N?
It's in the paragraph that starts with "Proof of Theorem". Basically, you can find a block that has open braces on more than half of the N slots and one block that has closed braces on more than half of the N slots. Therefore, at at least one slot, one has an opening brace and the other a closing brace.
I`ve got it. Thank you :)
I solved Div.1 C during the competition using the algorithm below:
4686935 is the solution which uses the above algorithm. The time complexity is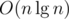 .
.
I made this by observation, not proof. How can I prove this algorithm is correct?
could you provide more details :)
Take a look at 3D - Least Cost Bracket Sequence.
.o. i have figured something while thinking about your equation. let's take always by block of size 2*n.
It is obvious that we are considering our options to change when we are at odd positions and we are changing the optimal positions before or equal to the current index which is yet unchanged.
now, let n=5. so, for first 10 positions the considering points would be: 1 2 3 4 5 6 7 8 9 10.
at position 1 we have no option but to change the 1st position. so, for the first block of 2n we have to consider the optimal answer with compulsory changing of 1st position, which is stored in V(2n).
But for the 2n blocks which will we join later, it may not be optimal to change the 1st bracket of those blocks. let's take for position 11 to 20. changing the 11th position may not be optimal. So, for the rest of 2n block we take V(3n) — V(n) in which our optimal answer is stored regardless of the change in 1st position of that block. the number of block yet to consider is (m/2 — 1). which is the next part of the equation.
Thanks for mentioning the greedy approach. :)
I found a different greedy solution which can be done in $$$O(n \log m)$$$.
Let's first put opening brackets everywhere. We need to pick $$$nm/2$$$ positions and put closing brackets there, so the bracket sequence will be regular and the sum $$$b_{j \bmod n} - a_{j \bmod n}$$$ for all picked positions $$$j$$$ is the least possible.
Observation 1. Consider a set of positions with the same remainder modulo $$$n$$$. Obviously, it's best to move all picked positions in this set to the right, so brackets in this set will look like "((($$$\ldots$$$)))" (the cost will not change and the sequence will stay regular).
Now, the greedy idea: let's sort all remainders $$$i$$$ by $$$b_i - a_i$$$ and going through each $$$i$$$ in this order let's try to pick as many positions with the remainder $$$i$$$ as possible (by observation 1, we'll be picking these positions from the right). To do that optimally, let's binary search the number of picked positions. Now we need to check that the sequence is regular given the number of picked positions for each remainder.
Observation 2. It suffices to check only first $$$n$$$ and last $$$n$$$ prefix balances.
Proof. Let $$$0 \ldots i$$$ be a prefix with a negative balance. If there is a whole block to the left, there might be two cases. If that block's balance is positive, then blocks before it are also positive, and thus prefix $$$0 \ldots i \bmod n$$$ is negative. If that block's balance is not positive, the blocks after it are also not positive, so we can move to the right until we are in the last block. The prefix will still be negative.
This here 97872815 is $$$O(n^2 + n \log m)$$$, but it can be done in $$$O(n \log m)$$$ with data structures.
We'll use matroids (maybe overkill). Call a set of positions independent iff the sequence with closing brackets in these positions is regular. Obviously, empty set is independent, a subset of an independent set is independent. Now let $$$A$$$ and $$$B$$$ be independent sets, such that $$$| A | < | B |$$$. Let $$$i$$$ be the largest position in $$$B \setminus A$$$. It's easy to see that adding $$$i$$$ to $$$A$$$ will not make the set dependent. So, it's a bona fide matroid and the greedy works.
In fact you can solve problem E in O(n\log n) time by using simple data structure.
Problem D can also be solved in O(n\log n) time by using offline algorithm.
Actually, problem D can be solved in O(NlogN) by an online algorithm. Check 4673602 for details.
It took me 2 days just to understand your code. Got to learn a ton of things from it. Thanks!
I'm glad you found it useful. Persistent data structures is a very interesting topic, you can find some other implementations of them here.
Thank you very much! :)
351A — Jeff and Rounding, I'm now stuck by a VERY VERY weird situation. Can anyone help me?
My approach is greedy and the code was almost the same with Kyuubi's. You can search "Kyuubi" in this page to see his greedy algorithm, which is the same as mine. Thank you Kyuubi :)
The thing is, my codes 4722053 and 4722088 have the same code but one got Ac in 30ms while the other got TLE. The only difference is, I put the last two lines in the for loop in 4722088 outside the loop, and created a new loop for them. It's just the difference between
and
It's driving me mad. Who can help me figure out why it makes such huge difference?
All these weird problem are caused by some careless error, like visiting a[-1], or the array is not bit enough, or a variable has not been initialized. I had a too small array. Please ignore my previous post.
I've found a simpler solution to '351E — Jeff and Permutation': First, substitute each number with its absolute value, then iterate through the numbers in the same order they were given and for each of them (lets call the currently processed number 'i'), count numbers with less absolute value than i that go before i, and numbers with less (absolute) value than i that go after i. If there are more numbers of the first kind, multiply i by -1.
Finally, count the inversions and print the number.
The solution can be implemented in O(n log n) with range trees, but the brutal approach passes the tests with O(n^2).
Can you please explain why this is correct ?
A number j that has higher or equal absolute value to i will form an inversion with i iff one of the following is true:
j goes before i in the input sequence and j is positive,
j goes after i in the input sequence and j is negative.
The above means that the sign of i doesn't change the number of inversions that it forms with numbers of higher or equal absolute values. (*) We can forget about them as far as choosing sign for i is concerned.
(**) A number j that has lower absolute value than i will form an inversion with i iff one of the following is true:
j goes before i in the input sequence and i is negative,
j goes after i in the input sequence and i is positive.
Analogically, yet a little bit different. ;) This means that signs of numbers of less absolute value than i doesn't change the number of inversions that they form with i. (***) We can choose a sign for i without worrying about what sign will these numbers be.
(*) and (***), brought together, let us come to the conclusion that the sign for i can be determined regardless of other numbers' signs. E.g. greedily, why not. ;)
The condition that lets us decide what sign to give to i is a straightforward implication of (*) and (**). (*) tells us that there's no need to worry about numbers with higher/equal absolute value to i. We know from (**) that to minimize the number of inversions that i forms, i should be negative iff there are more numbers of less absolute value that go before i than those that go after i.
Feel free to see my submission: http://codeforces.com/contest/351/submission/4958417
Jeff and Periods —
I am getting correct output on my computer but a wrong output in the codeforces. What could possibly go wrong? This has happened with be already for a different problem. Any solutions for this?
Are you sure you get right answer for test #5 on your computer? On my machine and on CF your code outputs sth wrong.
You don't check if(count >= 0) in one place. Check out this change
Sorry, My bad. I checked it wrong. I might have checked it wrong for that other problem too. Thanks a lot for understanding my entire code and helping me out :D
In C, Jeff and Rounding — I am getting a compilation error for stof(). I used #include<bits/stdc++.h> and GNU C++11 Why doesn't it compile?
IN PROBLEM 351B , could not understand . we have the formula for an answer ansI = 1 + 1 + ansI - 1 - 1 × 0.5 + ansI - 1 + 1 × 0.5 how we are calculating expectation using this formula
Suppose we have 'i' inversions at this time. Then during Jeff's turn i -> i-1 as he will always try to make the array sorted. But during Furik's turn 50% times i -> i-1 and 50% times i ->i+1.
So let the current state be dp[i];
Jeff's Turn : dp[i] = 1 + dp[i-1].
Now Furik's Turn : dp[i-1] = 1 + 0.5*dp[i-2] + 0.5*dp[i].
So, dp[i] = 1 + 1 + 0.5*dp[i-2] + 0.5*dp[i].
dp[i] = 4 + dp[i-2] (required recurrence)
Can someone Explain Jeff and Furik?
EV(n) = 1 + 0.5*(EV(n-2)) + 0.5*(2+EV(n))
EV(n) represent expected value for n inversions required. As Jeff starts the game so EV(n) should be equal to 1 + g where g is 0.5*(EV(n-2)) + 0.5*(2+EV(n)) (and now it's Furik's turn). If heads appears inversions reduces by 1 and if tails appears inversions increases by 1. so g = p(head)*EV(n-2) + p(tails)*(EV(n) + 2(as 2 turns are wasted))
Suppose we have 'i' inversions at this time. Then during Jeff's turn i -> i-1 as he will always try to make the array sorted. But during Furik's turn 50% times i -> i-1 and 50% times i ->i+1.
So let the current state be dp[i];
Jeff's Turn : dp[i] = 1 + dp[i-1].
Now Furik's Turn : dp[i-1] = 1 + 0.5*dp[i-2] + 0.5*dp[i].
So, dp[i] = 1 + 1 + 0.5*dp[i-2] + 0.5*dp[i].
dp[i] = 4 + dp[i-2] (required recurrence)
In 351B — Jeff and Furik, could you please explain why we can transform from
2 * ansI -ans(I-2)-4 = ansI
to ansI = 4 + ans(I - 2) ?
my question might sound a little stupid but, really,...
for example when we recursively call x = x + 1, we cannot transform to x-x = 1 <=> 0 = 1
Can anynyone clearly explain the recurrence of Div1 B jeff and furik??
Suppose we have 'i' inversions at this time. Then during Jeff's turn i -> i-1 as he will always try to make the array sorted. But during Furik's turn 50% times i -> i-1 and 50% times i ->i+1.
So let the current state be dp[i];
Jeff's Turn : dp[i] = 1 + dp[i-1].
Now Furik's Turn : dp[i-1] = 1 + 0.5*dp[i-2] + 0.5*dp[i].
So, dp[i] = 1 + 1 + 0.5*dp[i-2] + 0.5*dp[i].
dp[i] = 4 + dp[i-2] (required recurrence)
351D — Jeff and Removing Periods submission matching the editorial description.
For 351D — Jeff and Removing Periods, I wrote a blog. It's heavily based on rlac's submission.