I was trying to solve this problem : cf-497D
My solution idea : let $$$R_d(p) = p'$$$ where $$$p'$$$ is the new location of point $$$p$$$ if we rotate it $$$d$$$ degree counter-clockwise with respect to $$$(0,0)$$$. That mean $$$R_d(p) = pe^{id}$$$
Hence, for some point $$$a \in A$$$ and $$$b \in B$$$ we can write $$$R_d(a-p)+p = R_d(b-q)+q$$$.
$$$R_d(a-p)+p = R_d(b-q)+q$$$
$$$\Longrightarrow R_d(a)-R_d(p)+p = R_d(b)-R_d(q)+q$$$
$$$\Longrightarrow p-q - R_d(p) + R_d(q)= R_d(b)-R_d(a)$$$
$$$\Longrightarrow (p-q) \frac{R_d - 1}{R_d}= a-b$$$
Here , $$$(p-q) \frac{R_d - 1}{R_d}$$$ actually represent a circle($$$C$$$) centered $$$p-q$$$ and radius = $$$|p-q|$$$.
And $$$a-b$$$ = Minkowski sum of A and (-B) [if we consider all $$$a$$$ and all $$$b$$$ ].
Hence, the problem turns into, checking if circle $$$C$$$ intersects polygon A-B or not.
My first idea was to triangulate $$$A$$$ and $$$-B$$$ then calculate the Minkowski sum of each pair, then check if the polygon(sum) intersects with circle $$$C$$$ or not.
I've written this code. I used the triangulation method mentioned in Computational geometry algorithms and applications-Springer-Verlag Berlin Heidelberg (2008) [page: 49]. But got WA on test 7. 
Then I change my triangulation algorithm and use the Ear clipping method mentioned here. Here is my implementation($$$O(n^3)$$$). But again got WA on case 31.
I've read the editorial, and without triangulation, just take each pair of edges (one from $$$A$$$ and another one from $$$B$$$) and Minkowski sum them and got AC. My code.
Do we only need the borderline of the polygon here in this problem? or my triangulation code is wrong. Can you help me figure out, what have I done wrong, in the code? And please share your triangulation code(both $$$n^2$$$ and $$$nlogn$$$ [with line sweep]).
UPDATE: The main problem that was in my solution was a typo:
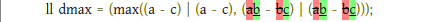
current submission: 178730641 — AC previous submission: 116207161 — WA










