120700765
This is similar to the solution suggested by OleschY, although uses single dfs per node.
Using the linearity of expectation, the answer to this problem is a sum of probability of inversion for each pair $$$i \lt j$$$.
For every node $$$i$$$, we can find this probability for each node $$$j \gt i$$$, as following:
Root tree at node $$$i$$$. Start DFS in $$$i$$$ that will calculate two following values for each node $$$v$$$: the size of subtree rooted at $$$v$$$, $$$sz(v)$$$ and the parent of $$$v$$$, $$$p(v)$$$.
Now consider every node $$$j \gt i$$$, as shown in the figure. What is the probability that it will be marked before marking node $$$i$$$? There are three cases:
1) With probability $$$sz(j)/n$$$ we will start in the subtree of $$$j$$$. Conditional on that, we will mark node $$$j$$$ earlier than node $$$i$$$ with probability 1.
2) We start in $$$i$$$ or any subtree of a child of $$$i$$$ rather than the one containing node $$$j$$$. In that case we reach node $$$i$$$ before $$$j$$$. So probability if inversion conditional on that is zero.
3) We start somewhere on the path from $$$i$$$ to $$$j$$$, or on any subtree branching from that path. Let's look on the picture: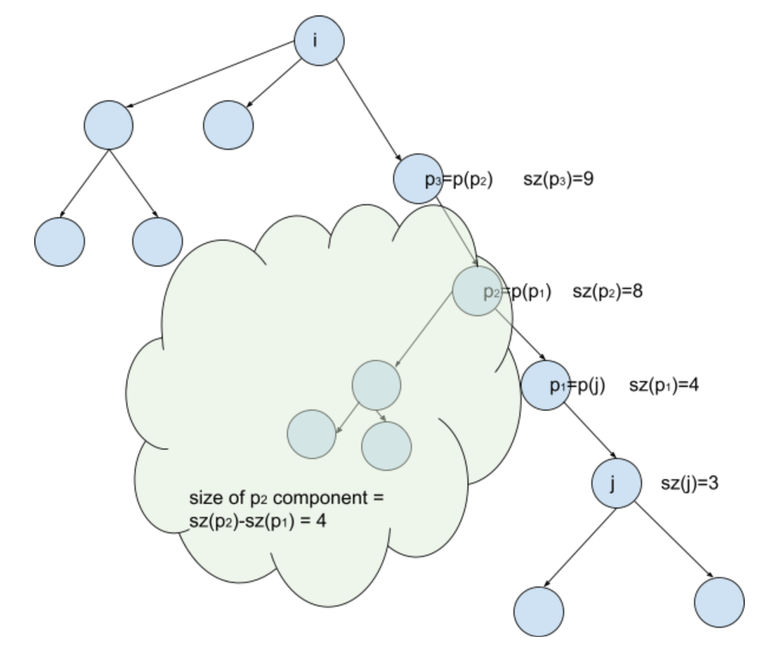
With probability $$$1/n$$$ we start at some node $$$p_k$$$. If we start at node $$$p_1$$$ we need one move down the path from $$$i$$$ to $$$j$$$ to get the inversion, or two moves up the path, to reach $$$i$$$ and to prevent inversion. Generally, if there are $$$m$$$ nodes on the path from $$$i$$$ to $$$j$$$ (excluding $$$i$$$ and $$$j$$$), $$$p_1$$$ — parent of $$$j$$$ ... $$$p_m$$$ -- child of $$$i$$$, then the probability of inversion conditional on starting in node $$$p_k$$$ is equal to the probability of throwing $$$k$$$ heads earlier than throwing $$$m+1-k$$$ tails. That is a known probability question, and the answer to it can be calculating recursively, as with equal probability we reduce the problem to that with one less head to get to the goal, or with one less tail to get to the goal. Let $$$x$$$ be the desired number of heads, and $$$z$$$ — the total length of path, $$$m+1$$$. Then
With border conditions $$$P(z,0) = 1$$$, $$$P(z,z) = 0$$$.
At last, what happens if we start in some subtree branching from the node on the path, as shown in the cloud on the picture? It turns out, that in that case, no matter when and whether we cover this whole branch, at some point we will be at node $$$p_2$$$ before moving along the $$$i-j$$$ path. So the aformentioned probabilities can be just weighted with the size of the tree branching from the node $$$p_2$$$ (shown in the cloud), which is calculated as $$$sz(p_2) - sz(p_1)$$$, or generally $$$sz(p_k) - sz(p_{k-1})$$$, where $$$p_0$$$ is node $$$j$$$ itself.
We can reconstruct the path easily, as we stored each parent while running DFS, and precompute $$$P(z,x)$$$ for all the values less than n. The total complexity is $$$O(n^3)$$$, as for every pair $$$i,j$$$ we processed the path from $$$i$$$ to $$$j$$$ which has length up to $$$n$$$.











Oh, I see, your main point is counting the nodes of the subtrees $$$sz(v)$$$ and using that to determine the size of the components with same 'root' (you call them $$$p_k$$$ components) on the $$$i-j$$$ path. That's clever, that could've saved me implementing a second clunky DFS, only need to iterate $$$i-j$$$ once!
On a side note, another possibility (which I have seen in the submissions of several highranked participants) is calculating the pairwise distances of all nodes with floyd warshall. Assume $$$p$$$ is in the $$$p_k$$$-component. Then we can easily calculate: $$$2 \cdot dist(j, p_k)=dist(p,j)+dist(i, j)-dist(p,i)$$$ (note, we do not need to know $$$p_k$$$ on the right hand side). That's another way to determine the distance components.